В работах по теории массового обслуживания системам с неодинаковыми возможностями рабочих органов уделено незаслуженно мало внимания, хотя в прикладных задачах подобные ситуации возникают достаточно часто. Даже в фундаментальной работе Т.Л. Саати [1], охватывающей очень широкий круг теоретических и прикладных проблем теории массового обслуживания, только упоминается о факте их существования. В статье [2] приведен общий вид графа для систем такого типа и показано, что с увеличением числа каналов число возможных состояний и, следовательно, размерность системы уравнений для отыскания соответствующих вероятностей возрастает в темпе геометрической прогрессии. Там же доложены результаты аналитического исследования двухканальной системы с неэквивалентными каналами, не имеющей опции накопления очереди, и предложен алгоритм рационального администрирования. К сожалению, возможности аналитического подхода ограничены кругом задач малой размерности в силу очевидных технических сложностей. Поэтому для анализа поведения систем с произвольным числом рабочих органов, а также систем с ожиданием, было принято решение обратиться к имитационному моделированию с использованием специализированного программного комплекса AnyLogic [3, 4], который хорошо зарекомендовал себя в практике исследований.
Целью исследования является изучение поведения систем массового обслуживания (СМО) с каналами различной интенсивности, разработка алгоритма эффективного администрирования подобных систем, а также доказательство существования таких наборов параметров систем, при которых эксплуатационные характеристики СМО с неэквивалентными каналами оказываются выше, чем в СМО с каналами равной интенсивности. Результаты исследования могут иметь прикладное значение во многих областях, в том числе в телекоммуникационных сетях [5].
Материалы и методы исследования
Рассмотрим сначала результаты, полученные в ходе имитационного моделирования трех- и четырехканальной СМО с неэквивалентными каналами, функционирующих в условиях пуассоновских потоков и не предусматривающих накопления очереди. Для систем такого типа наиболее важными и интересными в плане практического использования являются две характеристики. 1. Р0 – вероятность того, что система свободна. Этот показатель определяет степень напряженности работы системы и имеет смысл доли времени, в течение которого на обслуживании нет ни одной заявки. 2. Ротк – вероятность отказа, т.е. вероятность возникновения ситуации, когда все каналы находятся в режиме обслуживания, а значит, все заявки, пришедшие в это время, не попадают в систему. Этот показатель имеет смысл доли потерянных заявок.
В качестве базы сравнения были приняты соответствующие стационарные характеристики СМО с эквивалентными каналами, суммарная интенсивность которых равнялась суммарной интенсивности исследуемых систем. Для их вычисления использовались известные расчётные соотношения (например, [6]).
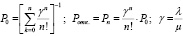, (1)
где n – число каналов обслуживания; λ – интенсивность входного потока заявок; µ – интенсивность потока обслуживания каждого из каналов, γ – величина нагрузки на систему.
Модель трехканальной системы в среде AnyLogic, в рамках которой были реализованы имитационные эксперименты, приведена на рисунке.
Данная модель состоит из блоков для создания (sourse), направления (selectOutput, selectOutput1, selectOutput2), задержки (delay, delay1, delay2) и уничтожения (sink, sink1, sink2, sink3) заявок на обслуживание.
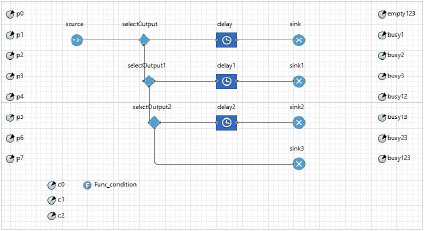
Схема трехканальной СМО с отказами
Помимо блоков, в модели используются переменные для подсчета вероятностей стационарных состояний (P0, P1, P2, P3, P4, P5, P6, P7), переменные для подсчета количества случаев для каждого возможного состояния системы (empty123, busy1, busy2, busy3, busy12, busy13, busy23, busy123). Для задания правила, по которому заявка направляется в тот или иной канал, используются переменные булевского типа (c0, c1, c2) и функция Func_condition().
В процессе имитационных экспериментов исследовалось поведение СМО с неэквивалентными каналами при различных значениях величины общей нагрузки на систему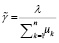 
и влияние соотношения интенсивностей отдельных каналов на эксплуатационные характеристики. Так же как в [2], в настоящей работе рассмотрены три варианта администрирования входного потока:
1. Поступившие заявки с равной вероятностью направляются на любой свободный канал.
2. Поступившие заявки распределяются по каналам с вероятностью пропорционально интенсивностям обслуживания.
3. При наличии нескольких свободных каналов поступившие заявки направляются на канал с наибольшей интенсивностью обслуживания.
Результаты исследования и их обсуждение
Результаты имитационного моделирования трёх- и четырехканальных СМО с отказами представлены в табл. 1 и 2 соответственно. Данные, полученные для первой схемы распределения входного потока, содержатся в графах S1, для второй схемы – в графах S2, для третьей схемы – в графах S3.
Анализ материалов табл. 1 и 2 позволяет указать на важные, по мнению авторов, свойства СМО с неэквивалентными каналами, о которых ранее не упоминалось. Прежде всего обращает на себя внимание то, что при небольшой величине общей нагрузки на систему (γ < 0,7) и выборе эффективной схемы распределения потока заявок, эксплуатационные характеристики систем с неэквивалентными каналами оказываются предпочтительнее по сравнению с системой той же суммарной интенсивности и одинаковыми каналами. Действительно, общая напряженность работы, определяемая величиной Р0, для трехканальной системы при γ = 0,222 выше базовой на 15 %, а при γ = 0,555 выше базовой на 4,4 %, а для четырехканальной при γ = 0,25 выше базовой на 28,7 %, а при γ = 0,4 на 21,3 %. Это может стать значимым фактором, например, при планировании графика технического обслуживания системы или при оценке возможности подключения дополнительных потоков.
Таблица 1
Результаты моделирования трехканальной СМО с отказами
|
λ |
μ1 |
μ2 |
μ3 |
Схема |
Р0 |
Ротк |
|
9 |
3 |
3 |
3 |
γ = 1 |
0,078 |
0,341 |
|
1 |
3 |
5 |
S1 |
0,047 |
0,371 |
|
|
S2 |
0,055 |
0,356 |
||||
|
S3 |
0,065 |
0,356 |
||||
|
2 |
3 |
3 |
3 |
γ = 0,222 |
0,520 |
0,025 |
|
1 |
3 |
5 |
S1 |
0,395 |
0,036 |
|
|
S2 |
0,493 |
0,028 |
||||
|
S3 |
0,598 |
0,020 |
||||
|
5 |
3 |
3 |
3 |
γ = 0,555 |
0,206 |
0,159 |
|
1 |
3 |
5 |
S1 |
0,133 |
0,184 |
|
|
S2 |
0,171 |
0,173 |
||||
|
S3 |
0,215 |
0,158 |
||||
|
15 |
3 |
3 |
3 |
γ = 1,666 |
0,026 |
0,531 |
|
1 |
3 |
5 |
S1 |
0,014 |
0,547 |
|
|
S2 |
0,016 |
0,543 |
||||
|
S3 |
0,018 |
0,542 |
Таблица 2
Результаты моделирования четырехканальной СМО с отказами
|
λ |
μ1 |
μ2 |
μ3 |
μ4 |
Схема |
Р0 |
Ротк |
|
20 |
5 |
5 |
5 |
5 |
γ = 1 |
0,028 |
0,318 |
|
1 |
4 |
6 |
9 |
S1 |
0,011 |
0,335 |
|
|
S2 |
0,016 |
0,329 |
|||||
|
S3 |
0,021 |
0,322 |
|||||
|
5 |
5 |
5 |
5 |
5 |
γ = 0,25 |
0,369 |
0,016 |
|
1 |
4 |
6 |
9 |
S1 |
0,207 |
0,027 |
|
|
S2 |
0,330 |
0,018 |
|||||
|
S3 |
0,475 |
0,010 |
|||||
|
8 |
5 |
5 |
5 |
5 |
γ = 0,4 |
0,207 |
0,057 |
|
1 |
4 |
6 |
9 |
S1 |
0,097 |
0,079 |
|
|
S2 |
0,161 |
0,066 |
|||||
|
S3 |
0,251 |
0,051 |
|||||
|
15 |
5 |
5 |
5 |
5 |
γ = 0,75 |
0,061 |
0,210 |
|
1 |
4 |
6 |
9 |
S1 |
0,023 |
0,239 |
|
|
S2 |
0,037 |
0,224 |
|||||
|
S3 |
0,054 |
0,210 |
Таблица 3
Результаты моделирования четырехканальной СМО в условиях изменяющейся интенсивности обслуживания
|
№ п/п |
μ1 |
μ2 |
μ3 |
μ4 |
Р0 |
Ротк |
|
1 |
5 |
5 |
5 |
5 |
0,207 |
0,057 |
|
2 |
1 |
4 |
6 |
9 |
0,251 |
0,051 |
|
3 |
1 |
3 |
7 |
9 |
0,250 |
0,048 |
|
4 |
1 |
2 |
8 |
9 |
0,233 |
0,055 |
|
5 |
1 |
2 |
3 |
14 |
0,221 |
0,061 |
|
6 |
2 |
4 |
6 |
8 |
0,272 |
0,046 |
|
7 |
3 |
4 |
6 |
7 |
0,261 |
0,048 |
Аналогичная картина наблюдается и с величиной Ротк, которая показывает долю потерянных заявок. При малых значениях γ потери явно меньше. Данный эффект будет особо значимым для систем, задействованных в обработке потоков больших данных. Подобные ситуации характерны в работе телекоммуникационных комплексов, системах обработки поисковых запросов и т.п.
Также представляет интерес исследование влияния перераспределения интенсивностей рабочих органов СМО на ее эксплуатационные свойства. С этой целью была реализована новая серия имитационных экспериментов, результаты которой представлены в табл. 3. Для четырехканальной системы при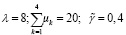 
были найдены значения Р0 и Ротк в различных комбинациях интенсивностей каналов обслуживания. Данные по потокам, распределенным в соответствии со схемами S1 и S2, в табл. 3 отсутствуют, поскольку схема S3, где приоритет отдается каналам с большей интенсивностью обслуживания, выглядит во всех отношениях предпочтительнее.
Данные, приведенные в табл. 3, свидетельствуют о заметном влиянии изменения интенсивности обслуживания на величину показателей Р0 и Ротк, которое не может быть отнесено на счет погрешностей моделирования. Так, в частности, напряженность работы систем по отношению к базе сравнения меняется от 6,8 до 31,4 % (строки 5 и 6), а доля потерянных заявок – от 7 до 19,3 %. Отсюда следует, что для любой величины общей нагрузки γ существует оптимальный набор интенсивностей обслуживающих устройств, при котором минимизируется количество потерянных заявок при сохранении приемлемого уровня напряженности работы системы. Естественно, что параметры такого набора строго индивидуальны для каждой конкретной СМО и могут рассматриваться в качестве паспорта ее эксплуатационных возможностей. Авторы не располагают сведениями об аналитических способах решения данной оптимизационной задачи, однако можно считать доказанным, что аппарат имитационного моделирования делает это возможным.
Из табл. 1 и 2 также видно, что с ростом величины общей нагрузки более 0,75 характеристики СМО с одинаковыми каналами становятся лучше соответствующих значений СМО с неэквивалентными каналами, хотя и в этом случае положительный эффект администрирования входного потока имеет место.
Учитывая результаты, полученные в ходе имитационного моделирования поведения систем с отказами, авторы решили ограничиться для систем, имеющих опцию накопления очереди, только материалами по четырехканальным системам при γ = 0,4. Для оценки работы таких систем важны два дополнительных показателя: число мест ожидания и средняя длина очереди – Lr . Последняя представляет собой не что иное, как математическое ожидание числа заявок в очереди, и может быть найдена по формуле
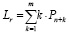, (2)
где m – количество мест в очереди.
Результаты соответствующих имитационных экспериментов содержатся в табл. 4.
Как и в табл. 3, по системам с неэквивалентными каналами представлены результаты только для наиболее эффективного варианта администрирования, предусматривающего приоритетную загрузку каналов с большей интенсивностью обслуживания.
Таблица 4
Результаты моделирования четырехканальной СМО с ожиданием
|
№ п/п |
μ1 |
μ2 |
μ3 |
μ4 |
Число мест в очереди |
Р0 |
Lr |
|
1 |
5 |
5 |
5 |
5 |
2 |
0,203 |
0,037 |
|
4 |
0,203 |
0,053 |
|||||
|
6 |
0,202 |
0,053 |
|||||
|
2 |
1 |
4 |
6 |
9 |
2 |
0,241 |
0,035 |
|
4 |
0,241 |
0,049 |
|||||
|
6 |
0,242 |
0,051 |
|||||
|
3 |
1 |
2 |
8 |
9 |
2 |
0,222 |
0,038 |
|
4 |
0,221 |
0,060 |
|||||
|
6 |
0,218 |
0,051 |
|||||
|
4 |
1 |
2 |
3 |
14 |
2 |
0,215 |
0,043 |
|
4 |
0,205 |
0,055 |
|||||
|
6 |
0,209 |
0,063 |
|||||
|
5 |
2 |
4 |
6 |
8 |
2 |
0,261 |
0,032 |
|
4 |
0,261 |
0,042 |
|||||
|
6 |
0,257 |
0,048 |
|||||
|
6 |
3 |
4 |
6 |
7 |
2 |
0,256 |
0,032 |
|
4 |
0,258 |
0,044 |
|||||
|
6 |
0,253 |
0,036 |
Анализ материалов табл. 4 позволяет утверждать, что добавление опции ожидания сохраняет за системами с неэквивалентными каналами меньший уровень напряженности работы. Причем, так же как для систем с отказами, упомянутый эффект тем меньше, чем больше различие между каналами с меньшей и большей интенсивностями обслуживания (результаты по блокам 4 и 6).
Вместе с тем, для показателя средней длины очереди Lr эффект от неэквивалентности каналов обслуживания наблюдается только тогда, когда различие между каналом большей интенсивности обслуживания и каналом меньшей интенсивности обслуживания сравнительно невелико (блоки 5 и 6 табл. 4). В противном случае либо имеет место обратный эффект, либо его вообще не удается обнаружить на фоне неустранимых погрешностей имитационных экспериментов.
Замечание. В отсутствие администрирования входного потока заявок все вышеупомянутые эксплуатационные характеристики у систем с неэквивалентными каналами становятся явно хуже, нежели у традиционных СМО с одинаковыми каналами. Предложенный алгоритм эффективного администрирования является основным признаком научной новизны настоящей работы.
Заключение
1. С помощью средств имитационного моделирования выполнен ряд экспериментов для трех- и четырехканальных систем массового обслуживания с каналами различной интенсивности, полученные результаты проанализированы в сравнении с системами, обладающими одинаковой интенсивностью каналов (табл. 1–4).
2. Предложен алгоритм администрирования потока заявок, в соответствии с которым заявки направляются с приоритетом на каналы, обладающие большей интенсивностью обслуживания. Экспериментально доказана эффективность данного алгоритма по критериям общей напряженности работы, доле обслуженных заявок и величине средней длины очереди.
3. Показано, что при небольшой величине общей нагрузки на систему системы массового облуживания с неэквивалентными каналами являются эффективнее систем с одинаковыми каналами. Вместе с тем при большом различии между интенсивностями каналов данный эффект не обнаруживается.