Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Для недоношенных новорожденных со сроком гестации менее 30 недель широко распространенным методом лечения является искусственная вентиляция легких (ИВЛ). Однако задержка перехода от инвазивной вентиляции легких к неинвазивной дыхательной поддержке может способствовать возникновению различного рода осложнений, повышенные риски ИВЛ-ассоциированных пневмоний и позднего сепсиса, возникновения эпизодов гипоксемии и гиперкапнии, брадикардии, нарушения мозгового кровотока и ателектаза, а также развитие в дальнейшем отклонений в неврологическом развитии ребенка [1, 2]. Ряд авторов отмечают, что успешность перехода с инвазивной на неинвазивную дыхательную поддержку составляет от 60 % до 86 % [3, 4]. Поэтому актуальной задачей является своевременный переход на неинвазивные методы лечения.

Однако принятие решения о переходе на неинвазивные методы лечения в настоящее время затруднено наличием многих недостаточно изученных факторов [5]. В результате врачи часто в таких случаях вынуждены при принятии решения также опираться на врачебный опыт и профессиональную интуицию, что может быть сопряжено с определенной долей ошибки. Поэтому представляет интерес использовать современные методы математического моделирования и многомерного статистического анализа и цифровые технологии [6–8]. Это облегчит врачам, независимо от уровня профессиональной подготовки и оснащенности современным оборудованием лечебного учреждения, выбор персонализированной терапевтической тактики для каждого пациента. Важным условием при этом является простота и доступность математических моделей для учреждений всех уровней оказания медицинской помощи.

В [9] описан метод оценки степени тяжести состояния недоношенных новорожденных со сроком гестации менее 30 недель. Он позволяет перед началом лечения оценить степень тяжести состояния здоровья, что позволяет выбрать инвазивный или неинвазивный вариант лечения. Однако остался нерешенным вопрос своевременного перехода с инвазивного на неинвазивный вариант лечения по индивидуальным показаниям пациента.

Цель данной статьи – разработка метода оценки состояния недоношенных новорожденных со сроком гестации менее 30 недель, позволяющего своевременно переводить их на неинвазивную респираторную поддержку.

Материалы и методы исследования

Из недоношенных новорожденных со сроком гестации менее 30 недель, проходящих лечение в ГУ «РНПЦ «Мать и дитя» (г. Минск), была сформирована обучающая выборка, состоящая из двух групп пациентов. В первую группу вошли 38 пациентов, которые все 7 дней наблюдения находились на ИВЛ (группа «ИВЛ» (Z = 0)). Во вторую группу вошли 14 пациентов, которые были переведены в течение этого периода на естественную вентиляцию легких (ЕВЛ) (группа «ЕВЛ» (Z = 1)) и стабильно находились в этом состоянии. Под стабильным состоянием считаем нахождение пациента не менее двух дней на ЕВЛ. Всего в выборке имеем 52 пациента. Решение задачи состоит в попытке определить момент снятия пациентов с ИВЛ, т.е. их перевода в группу «ЕВЛ».

В данные были включены: показатели анамнеза, кислотно-основного состояния (КОС) крови при рождении, а также ряд показателей текущего (посуточного) состояния здоровья пациентов. Анализируемые показатели приведены в табл. 1. Среднесуточные показатели брались как среднее значение за 7 суток (для группы «ИВЛ») и как среднее за последний день нахождения на ИВЛ (для группы «ЕВЛ»).

Схематично система мониторинга состояния пациентов, находящихся на ИВЛ, приведена на рисунке. Врач наблюдает за показателями состояния здоровья пациента и периодически при необходимости изменяет частоту искусственных вдохов, процент кислорода газовой смеси, подаваемой пациенту, и значение MAP либо принимает решение о переводе на неинвазивный вариант лечения по индивидуальным показаниям пациента.

Для практического использования методика оценки здоровья недоношенных новорожденных должна быть, с одной стороны, простой и понятной врачам. А с другой стороны, она должна опираться на достаточно строгую математическую модель, позволяющую легко интерпретировать полученные результаты. Этим условиям удовлетворяет логистическая регрессия [10, 11]. Однако для ее эффективного применения требуется удачно подобрать набор информативных признаков, позволяющих разделить множество наблюдений на кластеры.

Логистическая регрессия удобна тем, что позволяет формировать хорошо интерпретируемый показатель степени тяжести состояния здоровья в виде вероятности отнесения пациента к той или иной группе больных.

Таблица 1

Анамнестические и лабораторные данные

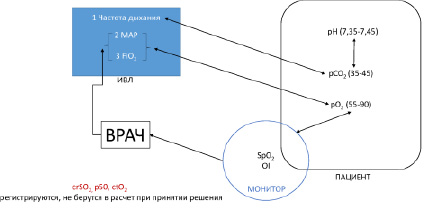
Система мониторинга состояния пациентов, находящихся на ИВЛ

Применительно к двум классам это выглядит следующим образом. Имеем обучающую выборку данных из n наблюдений

, ,

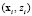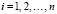где 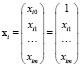– i-е наблюдение,

;

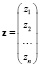
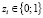– бинарная переменная, указывающая на принадлежность i-го наблюдения соответствующей группе (пусть первой группе при 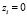и второй – при 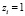); m – число признаков.

Введем логистическую функцию

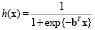, (1)

принимающей значения в интервале (0; 1) и выполняющей классификацию наблюдений. Пороговым значением для является .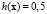

Разделяющая линейная граница задается уравнением гиперплоскости 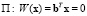, где 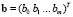– вектор коэффициентов.

Зададим область D1 возможных значений x для первой группы как 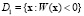, а для второй группы – как 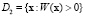. Тогда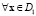 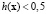и 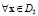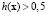. Если 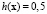, то x принадлежит гиперплоскости П, т.е. для произвольного наблюдения x* вероятность его отнесения к первой группе равна 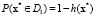, а ко второй – 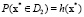. В нашем случае первая группа – это пациенты, находящиеся на ИВЛ (Z = 0), вторая группа – находящиеся на ЕВЛ (Z = 1). Оценивание вектора коэффициентов b было выполнено с помощью алгоритма Ньютона – Рафсона [12, 13].

Представляет интерес также исследование системных свойств каждой из групп пациентов с помощью энтропийного моделирования [14].

Результаты исследования и их обсуждение

Для решения задачи нужно построить решающее правило классификации между двумя группами пациентов «ИВЛ» и «ЕВЛ». Для этого нужно решить задачу многомерной классификации (распознавания) двух групп (кластеров) по показателям X1–X20. Суть решения состоит в нахождении такой совокупности показателей из исходного множества (X1–X20), которая позволила бы статистически достоверно распознать различия в этих группах. Решающее правило классификации получаем с помощью логистической регрессии.

Для обеспечения вычислительной устойчивости выполним стандартизацию исходных данных: для дискретных показателей приведем их значения к нулевому среднему, а для непрерывных – вычтем среднее и поделим на среднее квадратическое отклонение.

Информативными показателями оказались X1, X2, X3, X5, X7, X11, X12, X16–X20. Нормированные значения показателей приведены в табл. 2.

Стандартизация данных состоит в вычитании соответствующего значения a и делении на соответствующее значение b каждого из значений переменных (табл. 3).

Таблица 2

Фактические значения информативных показателей

Таблица 3

Параметры для стандартизации информативных показателей

Таблица 4

Коэффициенты интегративного прогностического индекса

Решающее правило строится по обучающей выборке. Решающее правило предназначено для классификации состояний новых пациентов с целью оперативного автоматического обнаружения момента перевода пациента с ИВЛ на ЕВЛ. В многомерном пространстве признаков оно имеет вид разделяющей поверхности. Воспользуемся логистической регрессией. Учитывая существенные признаки, был рассчитан интегративный прогностический индекс (ИПИ) по формуле

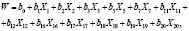(2)

где коэффициенты bj приведены в табл. 4.

Присутствие в прогностическом правиле (2) ряда показателей анамнеза и КОС крови при рождении свидетельствует о том, что они влияют на состояние здоровья пациентов. Также отметим, что в модель (2) не вошли управляющие показатели X1, X2, X3. Их статистическая незначимость может быть объяснена присутствием человеческого фактора.

Прогностическое правило (2) работает так. Если рассчитанный по формуле (2) результат будет меньше нуля, то у ребенка прогнозируется состояние «ИВЛ» с вероятностью 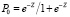. Если результат W будет больше нуля, то у ребенка прогнозируется состояние «ЕВЛ» с вероятностью 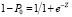. В табл. 5 приведены результаты классификации пациентов по ИПИ (1). Все пациенты правильно классифицированы.

Таблица 5

Результаты классификации пациентов

Все пациенты правильно классифицированы. Вероятности правильной классификации получились очень высокими, максимальная ошибка составила менее 0,04. Это означает, что классификация выполнена не только верно, но и статистически надежно.

Исследуем полученную математическую модель (2). Введем величину

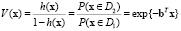, (3)

откуда нетрудно получить, что

, .

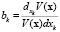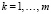Приравняем 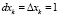и умножим обе части последней формулы на 100 %:

,

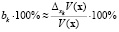с учетом (3) это означает, что коэффициент bk при переменной Xk показывает, на сколько процентов изменится отношение вероятности отнесения пациента к классу «ЕВЛ» (D2) к вероятности отнесения пациента к классу «ИВЛ» (D1) при увеличении Xk на одну единицу и при фиксированных значениях остальных переменных в (2).

Согласно (3) производная V(x) по Xk прямо пропорциональна коэффициенту bk. Поэтому для увеличения значения h(x) (вероятности отнесения пациента к классу «ЕВЛ») приращения 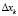должны быть положительными (если bk > 0) и отрицательными (если bk < 0): нужно увеличивать значения показателей X12, X17, X18; нужно уменьшать значения показателей X11, X16, X19, X20.

Это позволяет рассматривать задачу управления состоянием конкретного пациента с целью уменьшения времени нахождения его на ИВЛ с учетом его фактических показателей состояния здоровья. Целевой функцией будет вероятность h(x) отнесения пациента к классу «ЕВЛ». При h(x) > 0,5 пациент будет классифицирован как относящийся к классу «ЕВЛ».

Исследуем теперь поведение дифференциальной энтропии в каждой из групп пациентов. Результаты расчета [15] энтропии хаотичности HV, энтропии самоорганизации HR и общая энтропия H для двух групп пациентов приведены в табл. 6.

Таблица 6

Энтропийный анализ для групп «ИВЛ» и «ЕВЛ»

Из табл. 6 видим, что энтропия и ее составляющие в группах существенно отличаются. В группе «ЕВЛ» и энтропия хаотичности, и энтропия самоорганизации, и общая энтропия существенно меньше, чем в группе «ИВЛ». Это означает, что перед переходом к неинвазивной дыхательной поддержке у новорожденных происходит резкое уменьшение вариации (дисперсии) показателей и одновременный рост тесноты корреляционной связи между ними. Это позволяет предположить, что добавление к непрерывному мониторингу по правилу (2) энтропийного анализа для каждого из пациентов позволит повысить достоверность и оперативность перехода к неинвазивной дыхательной поддержке пациентов.

Заключение

Описана математическая модель для определения перехода недоношенных новорожденных со сроком гестации менее 30 недель от инвазивной вентиляции легких к неинвазивной дыхательной поддержке. Она основана на бинарной логистической регрессии.

Получено решающее правило для классификации состояний новых пациентов с целью оперативного автоматического обнаружения момента перевода пациента на неинвазивную дыхательную поддержку. Для обучающей выборки из 52 пациентов достоверность классификации составила 100 %.

Проведенный энтропийный анализ обучающей выборки пациентов показал, что перед переходом к неинвазивной дыхательной поддержке у новорожденных происходит резкое уменьшение вариации (дисперсии) показателей и одновременный рост тесноты корреляционной связи между ними.

Работа выполнена при поддержке совместного российско-белорусского проекта РФФИ (грант № 20-51-00001) и БРФФИ (грант № М20Р-008).