Одним из перспективных направлений в информатике и управлении сложными системами и процессами, активно развивающимся в последнее десятилетие, являются нейросетевые технологии обработки информации [1–3]. Применение нейросетей позволяет эффективно решать большое число разнообразных задач в различных технических приложениях. Нейросетевые алгоритмы обработки информации (НСАОИ) представляют собой эффективный набор программных средств обработки и анализа данных, но требуют настройки (обучения) для решения конкретных прикладных задач. От качества процесса обучения зависит эффективность применения нейросетевых алгоритмов обработки информации на стадии эксплуатации программного обеспечения.
Целью данной статьи является представление процесса обучения нейросетевых алгоритмов обработки информации с позиций системного анализа, предполагающего исследование вопросов управления качеством процесса обучения нейросетевых в рамках функционирования системы управления обучением нейросети на различных информационных базисах, как автономных, так и открытых, т.е. во взаимосвязи с изменяющейся внешней средой обучения.
Материалы и методы исследования
Моделирование процесса обучения НСАОИ
Под обучением НСАОИ понимается целенаправленный процесс адаптации параметров закона преобразования входных сигналов нейросети в выходной сигнал по критерию минимума ошибки, представляющей собой количественную меру расхождения фактического выхода нейросети с тестовыми значениями, задаваемыми при формировании обучающей выборки [4–6]. Иными словами, обучение НСАОИ есть такой подбор значений весов нейросети, при которых нейросеть функционирует с приемлемым для пользователя значением ошибки на всех элементах обучающей выборки.
Настраиваемые в ходе обучения веса нейросети представляют собой набор из весов искусственных нейронов, составляющих слои нейросети. При этом преобразование входных сигналов в выходной сигнал в отдельно взятом искусственном нейроне описывается выражением
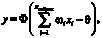 (1)
(1)
где y – выходной сигнал; ωi, 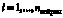 – веса преобразования входных сигналов в нейроне; θ – пороговый уровень реагирования нейрона на суммарный сигнал
– веса преобразования входных сигналов в нейроне; θ – пороговый уровень реагирования нейрона на суммарный сигнал 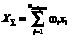 ;
; 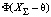 – функция активации. Совокупность весов всей нейросети обозначим
– функция активации. Совокупность весов всей нейросети обозначим 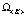 = <ω1, ω2,…, ωK>,; вход нейросети -
= <ω1, ω2,…, ωK>,; вход нейросети -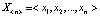 ; выход нейросети –
; выход нейросети – 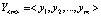 .
.
Опишем обучающую выборку («Training Sample Of Examples» (TSOE)) в виде множества пар входных и выходных обучающих сигналов:
TSOE = 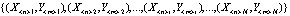 , (2)
, (2)
где 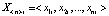 – i-й входной n-мерный обучающий сигнал;
– i-й входной n-мерный обучающий сигнал;
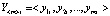 – i-й выходной m-мерный обучающий сигнал.
– i-й выходной m-мерный обучающий сигнал.
При обучении нейросети на i-м шаге обучения на ее вход подается i-й входной тестовый массив данных 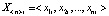 , в результате чего на выходе нейросети формируется i-й выходной сигнал
, в результате чего на выходе нейросети формируется i-й выходной сигнал 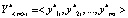 . Так как для каждого входного тестового массива данных
. Так как для каждого входного тестового массива данных 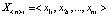 в TSOE задан выходной тестовый (опорный) массив данных
в TSOE задан выходной тестовый (опорный) массив данных 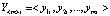 , то это позволяет вычислить вектор ошибок нейросети
, то это позволяет вычислить вектор ошибок нейросети
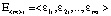 , (3)
, (3)
где 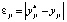 ,
, 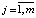 ;
; 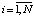 ,
,
и далее преобразовать его к скалярной оценке по правилу (4), либо (5):
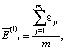 (4)
(4)
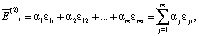
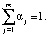 (5)
(5)
Для анализа значимости величины ошибки функционирования НСАОИ задается εПор – пороговое значение допустимой ошибки нейросети, после чего проверяется выполнение неравенств
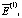 < εПор, либо
< εПор, либо 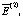 < εПор. (6)
< εПор. (6)
Если неравенство вида (6) не выполняется, то производится подстройка весов нейросети по алгоритму Al путем вычисления частных производных
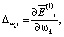 либо
либо 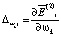 (7)
(7)
и коррекции значения весов по правилу:
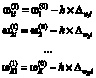 , (8)
, (8)
где <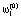 ,
, 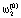 ,…,
,…, 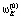 > – вектор начальных значений весов обучаемой нейросети;
> – вектор начальных значений весов обучаемой нейросети;
h – величина шага подстройки весовых коэффициентов нейросети.
Операции (7) и (8) повторяются, пока не будут выполнены условия (6).
Подстройка весов нейросети продолжается для всех примеров из TSOE.
После многократной отработки примеров происходит «стабилизация весов нейросети, при этом нейросеть дает удовлетворительные ответы на подавляющее большинство примеров из TSOE с заданной степенью «уверенности» 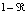 ,
, 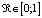 , где
, где 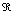 – вероятностный уровень остановки процесса обучения (т.е. процесс обучения останавливается, когда значение вероятности успешного обучения нейросети за время t достигает уровня 1-
– вероятностный уровень остановки процесса обучения (т.е. процесс обучения останавливается, когда значение вероятности успешного обучения нейросети за время t достигает уровня 1-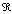 )».
)».
Модель процесса обучения НСАОИ представляет собой зависимость от времени текущей остаточной ошибки обучения (Current Residual Training Error), обозначаемой как CRTE и рассчитываемой по формулам (4) или (5). Вследствие действия неполностью контролируемых факторов значение CRTE в произвольный момент времени будет нормально распределенной случайной величиной с математическим ожиданием MCRTE(t) = 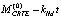 и среднеквадратическим отклонением
и среднеквадратическим отклонением 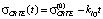 , где
, где 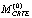 и
и 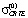 – начальные значения математического ожидания CRTE и, соотвественно, среднеквадратического отклонения CRTE при t = 0; klM и klσ – коэффициенты, характеризующие скорость уменьшения математического ожидания MCRTE(t) и среднеквадратического отклонения
– начальные значения математического ожидания CRTE и, соотвественно, среднеквадратического отклонения CRTE при t = 0; klM и klσ – коэффициенты, характеризующие скорость уменьшения математического ожидания MCRTE(t) и среднеквадратического отклонения 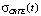 в процессе обучения.
в процессе обучения.
С учетом сделанных предположений процесс изменения во времени текущей остаточной ошибки обучения CRTE может быть математически описан нестационарным гауссовским случайным процессом с уменьшающимися значениями математического ожидания и среднеквадратического отклонения [6] (рис. 1).
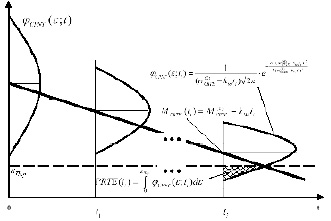
Рис. 1. Модель процесса обучения НСАОИ
Плотность распределения значений случайного процесса изменения CRTE в процессе обучения для произвольного временного сечения записывается как
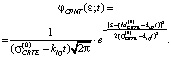 (9)
(9)
Результаты исследования и их обсуждение
Статические и динамические системы управления обучением нейросети, показатели качества их функционирования
Под системой управления обучением нейросети (СУОН) будем понимать совокупность объекта обучения – нейросетевого алгоритма обработки информации и элементов, реализующих процесс его обучения.
В зависимости от степени адаптивности характеристик системы управления обучением к состоянию объекта обучения будем различать два типа СУОН: статические и динамические.
Статическая система управления обучением нейросети содержит две составные части: объект обучения – НСАОИ и обучающую подсистему (рис. 2).
Обучающая система (рис. 3) содержит следующие основные элементы: обучающую выборку (TSOE); блок анализа ошибки функционирования НСАОИ на TSOE; блок подстройки весов НСАОИ; блок анализа показателей качества обучения НСАОИ на TSOE; блок формирования решения о завершении обучения НСАОИ на TSOE.
Статическая система управления обучением НСАОИ характеризуется заданными и неизменяемыми в процессе обучения следующими характеристиками: составом обучающей выборки TSOE (фиксированным множеством пар входных и выходных обучающих сигналов); жестко заданным алгоритмом Al подстройки весов НСАОИ; фиксированной величиной εПор (порогового значения допустимой ошибки нейросети) и заданным фиксированным значением 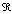 (вероятностного уровня остановки процесса обучения).
(вероятностного уровня остановки процесса обучения).
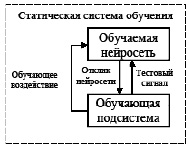
Рис. 2. Структура статической системы обучения НСАОИ
_fmt.jpeg)
Рис. 3. Статическая система обучения НСАОИ с развернутой структурой обучающей подсистемы
Качество функционирования статической системы обучения оценивается тремя показателями [6]: показателем результативности обучения PRTE (Probability of Reducing the Training Error), показателем оперативности обучения ATST (Average Time of Successful Neural Network Training) и показателем ресурсоемкости обучения WNRC (Weighted Average Normalized Resource Costs).
Показатель результативности обучения PRTE есть «вероятность снижения текущей остаточной ошибки обучения нейросети за время t до или ниже εПор (заданного порогового значения допустимой ошибки функционирования НСАОИ) при использовании алгоритма подстройки весов нейросети Al:
PRTE(Al ; εПор; t) = 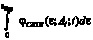 , (10)
, (10)
где
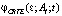 =
=
= 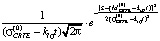 (11)
(11)
значение плотности распределения значений CRTE в произвольном временном сечении t».
Показатель оперативности обучения есть «среднее время успешного обучения нейросети при использовании алгоритма подстройки весов нейросети Al и при заданном пороговом значении допустимой ошибки функционирования εПор:
ATST(Al; εПор) = 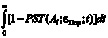 , (12)
, (12)
где PST((Al; εПор; t) = PRTE((Al; εПор; t)×PATSPP, т.е. вероятность успешного обучения нейросети (Probability of Successful Neural Network Training (PST)) за время t при применении алгоритма подстройки весов Al; PATSPP – вероятность адекватности обучающей выборки физической задаче (Probability of Adequacy of the Training Sample to the Physical Problem)».
Показатель ресурсоемкости обучения есть [7] «средневзвешенные нормированные затраты ресурсов (вычислительных ресурсов на реализацию процесса подстройки весов нейросети и временных затрат на формирование обучающей выборки TSOE):
WNRC (Al) = δ1×NCCR(Al) + δ2×NTC(Al), (13)
где NCCR(Al) – Normalized Cost of Computing Resources – нормированные затраты вычислительных ресурсов на реализацию процесса подстройки весов нейросети c использованием алгоритма Al; NTC(Al) – Normalized Time Costs – нормированные временные затраты на реализацию процесса подстройки весов нейросети c использованием алгоритма Al».
Адаптация в статической системе обучения нейросети распространяется только на настройку весов нейросети с целью обеспечения преобразования входных сигналов нейросети в выходной сигнал с допустимой ошибкой, определяемой строго на фиксированных элементах обучающей выборки ограниченного объема.
Решение о завершении обучения в статической СУОН формируется, когда значение вероятности PRTE(Al; εПор; t) достигает уровня 1-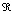 .
.
Достоинством статической СУОН является относительная простота реализации процесса обучения нейросети. Вместе с тем ей присущ ряд существенных недостатков:
1. Формальная зависимость показателей результативности и оперативности обучения от задаваемого значения εПор – порогового значения допустимой ошибки нейросети. При увеличении εПор для одного и того же значения времени обучения t' увеличивается значение PRTE(Al; εПор; t'), так как данная вероятность рассчитывается как интеграл от участка плотности распределения значений CRTE, лежащего ниже εПор (рис. 1). Формально при увеличении εПор результативность обучения возрастает и одновременно повышается его оперативность (рис. 4 и 5). Однако в действительности кажущееся улучшение качества обучения таковым не является, так как достигается за счет увеличения допустимой ошибки обучения, что объективно снижает фактическое, а не формальное качество обучения (нейросеть хорошо обучается работать плохо).
2. Обучающая выборка TSOE должна быть адекватна по объему испытаний и степени репрезентативности физической задаче, для выполнения которой обучается нейросеть. В противном случае при применении обученной по некачественной выборке нейросети будут возникать неприемлемые для пользователя ошибки.
Перечисленные недостатки статических СУОН обусловили разработку и применение динамических систем управления обучением нейросетей.
Динамическая система управления обучением нейросети помимо объекта обучения – НСАОИ и обучающей подсистемы содержит (рис. 6) пользователя и подсистему адаптации процесса обучения.
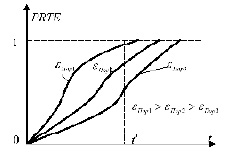
Рис. 4. Зависимость PRTE от времени обучения при различных пороговых значениях допустимой ошибки нейросети
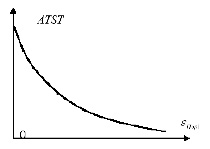
Рис. 5. Зависимость ATST от порогового значения допустимой ошибки нейросети
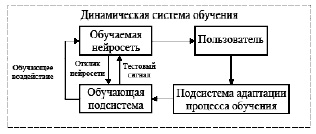
Рис. 6. Структура динамической системы обучения НСАОИ
Динамическая система обучения НСАОИ с развернутой структурой обучающей подсистемы представлена на рис. 7.
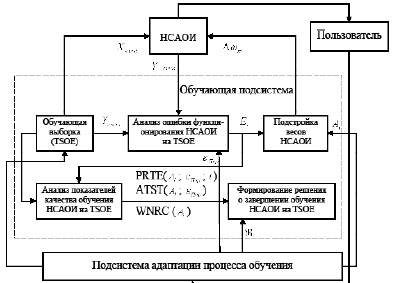
Рис. 7. Динамическая система обучения НСАОИ с развернутой структурой обучающей подсистемы
Динамическая система управления обучением НСАОИ характеризуется следующими особенностями:
– адаптируемым составом обучающей выборки TSOE (дополняемым при необходимости множеством пар входных и выходных обучающих сигналов);
– адаптируемым алгоритмом Al подстройки весов НСАОИ [8];
– адаптируемой к предпочтениям пользователя величиной εПор (порогового значения допустимой ошибки нейросети);
– адаптируемым к предпочтениям пользователя значением 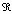 (вероятностного уровня остановки процесса обучения).
(вероятностного уровня остановки процесса обучения).
Качество функционирования динамической системы обучения помимо трех показателей качества статической системы (PRTE, ATST и WNRC) дополнительно характеризуется степенью адаптации характе- ристик обучающей подсистемы к допол- нительной информации о результатах функ- ционировании НСАОИ по назначению.
Степень адаптивности динамической системы обучения выше по сравнению со статической системой, которая использует только априорную информацию в виде обучающей выборки TSOE и первичные представления о пороговом значении допустимой ошибки нейросети. Динамическая система обучения адаптируется к апостериорной информации, которая появляется после того, как НСАОИ начинает испытываться, а затем и применяться по назначению.
Соответственно, можно очертить границы применимости статических и динамических систем обучения НСАОИ. Статические системы обучения целесообразно использовать на ранних этапах разработки НСАОИ для отработки алгоритмов обучения проектируемой нейросети. Динамические же системы обучения необходимо применять на стадии испытаний и эсплуатации НСАОИ для более точной настройки их на особенности реальных физических объектов и повышения фактической, а не расчетной эффективности целевого применения.
Заключение
Таким образом, в данной статье представлены результаты, позволяющие с позиций системного анализа исследовать возможности реализации управления качеством процесса обучения нейросетевых алгоритмов обработки информации на стадиях их проектирования, испытаний и эксплуатации. Введено понятие системы управления обучением нейросети. Предложено рассматривать два класса систем управления обучением: статические системы с фиксированными параметрами и динамические системы с адаптируемыми параметрами обучающей подсистемы. Описана структура статических и динамических систем, приведены их преимущества и недостатки, предложены показатели качества обучения для статических и динамических систем.



