Научно-технический прогресс влечет широкое внедрение информационных технологий во все области жизнедеятельности общества. Современные информационные системы осуществляют не только обработку данных, но поддержку различных сервисов и приложений, предоставляющих доступ конечным пользователям. Одной из проблем современных высоконагруженных информационных систем является потребность в больших объемах вычислительных ресурсов. Для обеспечения непрерывного доступа к информационным системам требуется решить проблему эффективного распределения между сервисами ограниченного объема ресурсов [1].
На сегодняшний день существует множество предприятий с корпоративной сетью, состоящей из большего числа конечных рабочих мест пользователей и серверного парка. Для рабочих мест пользователей выделяются компьютеры, которые чаще всего уступают по техническим характеристикам компьютерам, используемым в парке серверов. За счет использования множества приложений и размещения данных, в том числе не относящихся к работе, пользователи рабочих мест полностью загружают процессор и занимают все дисковое пространство компьютера. Для удовлетворения постоянно меняющихся бизнес-требований организации должны инвестировать больше времени и бюджета для масштабирования ИТ-инфраструктуры. Однако достижение этой цели за счет собственных средств и инвестиций не только не является экономически эффективным, но и организации не смогут обеспечить оптимальное использование ресурсов. Эти проблемы вынудили компании искать некоторые новые альтернативные технологические решения. Одной из таких современных технологий являются облачные вычисления на виртуальных машинах, которые направлены на увеличение вычислительной мощности и позволяют функционировать нескольким операционным системам вместе со всеми ее службами на одном физическом компьютере.
Виртуальная машина – виртуальная среда, которая функционирует как виртуальная компьютерная система с собственным процессором, памятью, сетевым интерфейсом и хранилищем, созданная на физическом аппаратном комплексе (расположенном за пределами или в локальной среде). Технология виртуализации позволяет совместно использовать систему со многими виртуальными средами. Гипервизор управляет оборудованием и отделяет физические ресурсы от виртуальных сред. Ресурсы секционируются по мере необходимости от физической среды до виртуальных машин. Когда виртуальная машина запущена, и пользователь или программа направляет запрос, требующий дополнительных ресурсов из физической среды, гипервизор адресует запрос к ресурсам физической системы, чтобы операционная система и приложения виртуальной машины могли получить доступ к общему пулу физических ресурсов. Благодаря применению технологии виртуальных машин серверный парк может быть существенно оптимизирован, что в итоге приведет к уменьшению объема используемых ресурсов и соответственно затрат на их поддержку.
В связи с этим целью данной работы является разработка и исследование математической модели процесса потребления основных вычислительных ресурсов при применении технологии виртуальных машин с целью повышения эффективности их использования.
Модели и методы теории массового обслуживания широко применяются при решении задач о распределения ресурсов [2–6]. В [2] разработана и анализирована облачная архитектура в виде двух систем массового обслуживания, показано, что такие модели могут быть очень полезными для настройки производительности. В [3] представлена модель для анализа производительности, подходящая для исследования качества услуг облачного сервиса, с использованием взаимодействующих стохастических моделей. Автор рассмотрел влияние различных параметров, включая скорость прибытия, время обслуживания запросов и его размер. В [4] представлена модель в виде системы массового обслуживания с высокоинтенсивным входящим потоком запросов. Такая модель более реалистична, так как учитывает свойства поступающих запросов и характеристики облачного центра. Авторы описали новое аналитическое приближение для оценки производительности центра облачных вычислений. В [5] представлен обзор моделей облачных вычислений с использованием систем массового обслуживания с различными механизмами распределения ресурсов. Несмотря на обширный обзор моделей в [5], эти модели не являются исчерпывающими, они мотивируют и открывают исследователям еще больше идей для моделирования с использованием систем массового обслуживания.
В работе предлагается новая модель для исследования процесса потребления вычислительных ресурсов при выполнении пользовательских задач виртуальными машинами.
Математическое описание модели
В качестве математической модели процесса потребления виртуальной машиной вычислительных ресурсов при обработке запросов пользователей рассмотрим бесконечно линейную систему массового обслуживания M|M|∞ [7]. На вход системы M|M|∞ поступает простейший поток запросов интенсивности λ, при этом время обслуживания запросов пользователей распределено по экспоненциальному закону с параметром µ (рисунок).
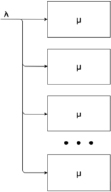
Система массового обслуживания M/M/∞
При поступлении запроса пользователя (заявки) на виртуальную машину (система) для его обслуживания выделяется некоторый объем вычислительных ресурсов (например, оперативной памяти), которые полностью освобождаются, когда запрос покидает систему. Если в момент поступления запроса недостаточно ресурсов у виртуальной машины для его обработки, запрос пользователя теряется.
Процесс функционирования системы можно описать двумя случайными процессами: число обсуживаемых запросов k(t) и объем свободных ресурсов S(t). Будем считать, что потенциальный поток запросов пользователей к виртуальной машине является бесконечным.
Рассмотрим процесс изменения состояний случайных процессов k(t) и S(t) с течением времени t. Изменение числа обслуживаемых запросов и объема свободных вычислительных ресурсов происходит в следующих случаях:
1) на виртуальную машину поступает новый запрос. Вероятность того, что за время Δt на виртуальную машину поступит новый запрос, определяется по формуле:
λΔt + o(Δt). (1)
Очевидно, что каждый новый запрос связан с захватом некоторого объема ресурсов φ для его обработки. Размер φ является случайной величиной с функцией распределения Fφ(x) и моментами M{φ} = a1 и M{φ2} = a2;
2) в случайный момент времени запрос полностью обрабатывается виртуальной машиной.
Продолжительность обработки запроса определяется функцией распределения:
F(x) = 1 – e–μt. (2)
После обработки запрос с интенсивностью μ покидает виртуальную машину независимо от продолжительности обслуживания других запросов. Тогда за время Δt запрос покидает машину с вероятностью:
kμΔt + o(Δt). (3)
Каждый обслуженный запрос освобождает ресурсы некоторого объема η. Размер η является случайной величиной с функцией распределения Fη и с моментами M{η} = c1 и М{η2} = c2.
Будем предполагать, что при завершении обработки пользовательского запроса вычислительные ресурсы освобождаются полностью, т.е. в том объеме, в котором они были захвачены изначально. Тогда в данных предположениях, очевидно, a1 = c1, а a2 = c2.
Определим i(t) как случайный процесс, который характеризует число пришедших запросов за время t, а l(t) – число запросов, завершающих обслуживание в момент времени t. Отсюда следует, что изменение объема свободных ресурсов можно описать выражением:
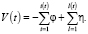(4)
Тогда общий объем ресурсов сервера составит:
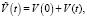
где V(0) – начальный объем свободных вычислительных ресурсов.
В дальнейшем, применяя методы теории массового обслуживания [7], а также подход, подробно описанный в [8, 9], проведено исследование двумерного процесса {l(t)i(t)}. Данный подход включает следующие этапы.
Этап 1. Составляется система дифференциальных уравнений Колмогорова для вероятностей состояний. При составлении системы используется следующее правило. В левой части уравнения стоит производная вероятности i-го состояния. В правой части – сумма произведений вероятностей всех состояний на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния). Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени.
Этап 2. Производится переход от рассмотрения распределения вероятности к его производящей функции. Из системы дифференциальных уравнений Колмогорова записывается дифференциальное уравнение в частных производных первого порядка для производящей функции.
Этап 3. Методом характеристик находится решение дифференциального уравнения, полученного на этапе 2, и записывается аналитический вид производящей функции.
Этап 4. В теории вероятностей и статистике характеристическая функция любой случайной величины полностью определяет ее распределение вероятностей. Характеристическая функция обеспечивает основу альтернативного маршрута для аналитических результатов по сравнению с работой непосредственно с функциями плотности вероятности или функциями распределения. На этом этапе производится переход от рассмотрения производящей функции к рассмотрению характеристической функции. Записывается аналитический вид характеристической функции.
Этап 5. Используя тот факт, что производная k-го порядка в нуле от характеристической функции равна начальному моменту k-го порядка, умноженному на k-ю степень мнимой единицы, находятся моменты первого и вторых порядков (математическое ожидание и дисперсия).
Продемонстрируем ключевые моменты этапов исследования.
Для распределения вероятностей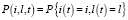 
составлена система дифференциальных уравнений Колмогорова:
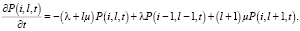
Откуда для производящей функции вида
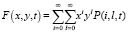
c начальными условиями
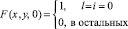
получено обыкновенное дифференциальное уравнение в частных производных первого порядка:
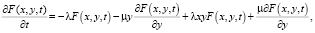
решая которое, запишем
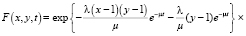
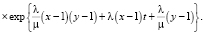
В результате определен вид производящей функции двумерного распределения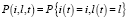 
. Объем свободных вычислительных ресурсов в произвольный момент времени вычисляется по формуле (4). Характеристическая функция этой величины имеет вид:
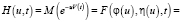
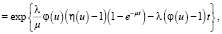
где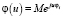 
– характеристическая функция величины φi, 
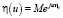– характеристическая функция величины ηi, j – мнимая единица.
Для нахождения вероятностных характеристик математической модели был применен метод моментов, изложенный в [6].
Нахождение вероятностных характеристик числа обслуживаемых запросов
Зная, что производная первого порядка в нуле от характеристической функции равна начальному моменту первого порядка, умноженному на первую степень мнимой единицы, найдем среднее значение свободных ресурсов для виртуальной машины:
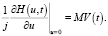
Учитывая, что:
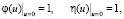
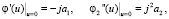
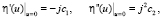
проведя несложные преобразования, нашли:
,
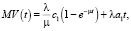
где V(0) – начальный объем свободных ресурсов.
Проведя аналогичные операции для определения второго начального момента, найдем дисперсию:
Учитывая, что вычислительные ресурсы освобождаются полностью, когда запрос покидает систему, т.е. a1 = c1, а a2 = c2, запишем итоговые выражения:
(5)
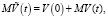
где V(0) – начальный объем свободных вычислительных ресурсов,
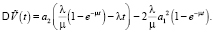(6)
Результатом этого раздела являются выражения (5) и (6), определяющие вероятностные характеристики величины объема свободных ресурсов, а именно математическое ожидание и дисперсию.
Заключение
В данной статье была разработана математическая модель процесса потребления ресурсов при обработке пользовательских запросов виртуальной машиной в виде системы массового обслуживания с неограниченным числом обслуживающих приборов, с простейшим входящим потоком заявок и экспоненциальным временем обслуживания их на приборах. Определены вероятностные характеристики величины объема свободных ресурсов сервера, а именно математическое ожидание и дисперсия.
С опорой на полученные в данной работе результаты в дальнейшем планируется усложнить данную модель, тем самым приблизив её максимально к реальным процессам, что создаст базу для дальнейшего изучения работы с ресурсами виртуальной машины с целью повышения эффективности их использования.