Социальные сети стали неотъемлемой частью жизни многих людей. Аудитория многих социальных сетей превышает население целых стран (рисунок). Согласно исследованию, которое провело аналитическое агентство Statista, в апреле 2019 г. самой популярной социальной сетью стал Facebook с 2,32 миллиарда активных пользователей в месяц [1].
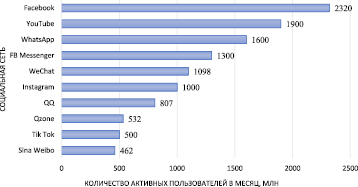
Рейтинг социальных сетей по количеству активных пользователей в месяц
Каждая социальная сеть сталкивается со спамом и вынуждена всячески бороться с подобными злоупотреблениями. Объем контента, который генерируется пользователями, действительно очень большой. Например, количество сообщений, которыми каждый день обмениваются пользователи социальной сети «ВКонтакте», достигает 10 миллиардов [2]. Вместе с ростом количества активных пользователей, как правило, происходит и рост количества создаваемого контента.
Развитие таких технологий, как классификация, нейронные сети, во многих случаях позволяют достоверно определить спам, но остается множество подозрительного контента, решение по которому должен принять человек – модератор.
Задача фильтрации спама остается важной и актуальной на текущий момент, так как доля спама в почтовом трафике остается на высоком уровне, а количество пользователей социальных сетей, мессенджеров и других сервисов, где присутствует спам, продолжает расти. Пользователи в свою очередь создают все больше контента, который нужно обрабатывать сервисам, в том числе и путем ручного модерирования. В Facebook для этой цели в 2017 г. работало 4500 модераторов, а в 2018 г. их насчитывалось уже 7500 [3]. Важность отсутствия ошибок первого рода, то есть классификация хорошего объекта как плохого, не позволяет использовать полностью автоматические системы, и часть объектов, оцененных как подозрительные, необходимо отправлять на прохождение ручного модерирования. Использование кластеризации позволит обрабатывать не каждый объект отдельно, а формировать кластеры, которые позволили бы принимать решение не по отдельно взятому документу или объекту, а по целому кластеру схожих по тем или иным параметрам документов или объектов. Такой подход позволит существенно сократить среднее время модерирования, а значит и повысить оперативность фильтрации спама.
Группировать можно не только такие объекты, как текст сообщения, изображения, но и пользователей, например на основе их действий и времени задержки между ними. Кластеризация позволяет оценивать группу объектов вместе, а не каждый объект в отдельности. В случае с ручным модерированием это позволяет существенно оптимизировать и повысить эффективность данного процесса. Группировать можно не только одинаковые объекты, но и похожие, что является как преимуществом, так и недостатком. С одной стороны, это позволяет объединить схожий спам в один кластер, но, с другой стороны, добавление к хорошему объекту элементов спама может привести к тому, что кластер будет состоять как из хороших объектов, так и из плохих.
Цель исследования: изучение возможности применения алгоритмов кластеризации для оптимизации противодействия спама в социальных сетях.
Материалы и методы исследования
Для проведения исследования необходимо: осуществить математическую постановку задачи кластеризации, провести обзор существующих алгоритмов кластеризации, рассмотреть опыт применения кластеризации для борьбы со спамом и нежелательным контентом.
Математическая постановка задачи. Если необходимо разделить некоторую выборку на непересекающиеся друг с другом подмножества, именуемые «кластерами», то мы сталкиваемся с таким понятием, как формальная постановка задачи кластеризации. Математически ее можно описать следующим образом.
Допустим, что существует множества X и Y, где X состоит из объектов, а Y содержит номера, имена или метки кластеров. Функцию расстояния между объектами внутри X зададим как p (x, xapos;). Также существует выборка объектов, которая конечна и служит для обучения – Xm = {x1,..., xm}. Провести кластеризацию – значит разбить начальную выборку на непересекающиеся подмножества. Они будут называться кластерами и будут разделены таким образом, чтобы каждый из них содержал объекты, близкие по метрике p. При этом объекты различных кластеров должны значительно отличаться. Во время кластеризации каждому объекту xi из обучающей выборки Xm присваивается определенный номер y1, являющийся номером кластера.
Общий подход применения кластеризации включает этапы:
1. Выборка объектов для последующей кластеризации.
2. Формирование переменных, по которым будет производиться оценка объектов в отобранной выборке. При необходимости значения переменных нормализуют.
3. Производится вычисление мер сходства объектов.
4. Применяется непосредственно кластерный анализ – формируются группы (кластеры) близких объектов.
5. Результаты анализа представляются в том или ином виде.
6. Корректируются отобранные метрики или метод кластерного анализа, чтобы получить оптимальный результат. Этап производится по необходимости.
Для оценки мер схожести объектов используют расстояние между ними. Расстояние между парами объектов можно измерять множеством метрик. Самые распространенные: евклидово расстояние, квадрат евклидова расстояния, манхэттенское расстояние, иначе называемое расстоянием городских кварталов, расстояние Чебышева и степенное расстояние.
Рассмотрим алгоритмы и методы формирования кластеров.
Метод k-средних. Алгоритм разбивает элементы множества на известное число кластеров, при этом минимизирует суммарное квадратичное отклонение точек кластеров от их центров. Каждое новое разделение на кластеры происходит с вычислением центра масс кластеров из предыдущей итерации. После чего происходит следующее разбиение на кластеры и так до тех пор, пока центр масс не изменяется.
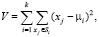
где k – число кластеровk – число кластеров, Si – полученные кластеры, i = 1, 2, …, k и µi – центры масс векторов xj∈Si.
Недостатками такого способа можно считать тот факт, что при таком разбиении на кластеры V – глобальный минимум суммарного квадратичного отклонения – не достигается. Достижимы только локальные минимумы. Кроме того, начальный выбор центров каждого из кластеров оказывает решающее влияние на конечный результат. Оптимального же метода выбора центров не существует. Еще одним недостатком такого подхода можно назвать необходимость знать заранее число кластеров для разбиения.
Метод k-медиан. В методе k-медиан для определения центра кластера вместо среднего значения вычисляется медиана множества. Задача разбиения кластеров по методу k-медиан заключается в нахождении центров кластеров так, чтобы полученные кластеры были компактны. Центры кластеров выбираются так, чтобы сумма расстояний между точками данных до центров кластеров была минимальна.
EM (expectation maximization). Существует алгоритм, перешедший в кластерный анализ из вероятностных моделей. Так называемый EM-алгоритм. Применяется тогда, когда модель зависит от скрытых переменных и находит оценки максимального правдоподобия параметров модели. Он состоит из итераций, каждый из которых производится в два шага – E-шаг и M-шаг. На первом шаге рассчитывается значение функции правдоподобия. Скрытые переменные при этом рассматриваются как наблюдаемые. На втором шаге находится оценка максимального правдоподобия. После чего это значение используется для первого шага на второй итерации.
Алгоритмы FOREL. Идея алгоритма заключается в объединении объектов в один кластер в зонах их сгущения. Разбиваются объекты таким образом, чтобы сумма расстояний от объектов кластеров до центров была минимальной по всем кластерам. На каждом шаге выбирается объект, раздувается вокруг него сфера, внутри которой выбирается центр тяжести, становящийся центром новой сферы. Так при каждой итерации центр смещается в сторону сгущения объектов. В тот момент, когда центр станет стабильным, объекты, находящиеся внутри полученной сферы, считаются кластеризованными и убираются из рассмотрения. Процесс повторяется, пока все объекты множества не будут кластеризованы. Минимизируемый алгоритмом функционал качества:
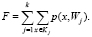
Нечеткая кластеризация C-средних. Подход кластеризации по c-средним позволяет разбивать множество на заданное количество нечетких множеств. В методе используется нечеткая матрица принадлежности с некоторыми элементами, которые определяют принадлежность определенного элемента начального множества конкретному кластеру.
Иерархическая кластеризация. Кластеризация с помощью иерархических алгоритмов позволяет использовать теорию графов для разделения множества объектов. В результате такого разбиения получается иерархия, иначе называемая дендрограммой.
Существует несколько подходов к иерархическому разбиению. В основном они характеризуются направленностью роста иерархий. Различают одиночную и полную связь. Одиночная связь (single-link), или метод ближайшего соседа: каждый шаг объединяет два кластера с самым маленьким расстоянием между двумя объектами. Полная связь (complete-link) иначе называется методом дальнего соседа. Характеризуется объединением двух расположенных максимально далеко друг от друга представителей. Различают еще метод средней связи (middle-link), являющийся комбинацией двух предыдущих подходов.
Алгоритм минимального покрывающего дерева. При реализации алгоритма минимального покрывающего дерева все экземпляры сначала помещаются в общий кластер, после чего происходит несколько итераций кластеризации. На каждой из них кластеры разделяются на два таким образом, чтобы расстояние между ними было наибольшим. Алгоритм наиболее подходит для выделения кластеров типа сгущений или лент. Другим недостатком данного алгоритма является высокая трудоемкость.
Послойная кластеризация. Еще одним примером графовой кластеризации является послойная кластеризация. В этом методе выделяются связанные компоненты. Из начальных данных формируется поочередно несколько подграфов, отражающих структурную иерархию связей. Связанные компоненты графа определяются порогом расстояния, которое как раз формирует новые кластеры. Изменяя уровень расстояний, можно варьировать степень глубины иерархии новых кластеров. Итоговые результаты сравнения алгоритмов представлены в таблице.
Сравнительная таблица алгоритмов кластеризации
|
Алгоритм кластеризации |
Форма кластеров |
Входные данные |
Результаты |
|
k-средних |
Гиперсфера |
Число кластеров |
Центры кластеров |
|
k-медиан |
Гиперсфера |
Число кластеров |
Центры кластеров |
|
EM |
Гиперсфера |
Число кластеров |
Матрицы, содержащие обновляемые параметры смеси |
|
FOREL |
Гиперсфера |
Радиус поиска локальных сгущений |
Центры кластеров |
|
С-средних |
Гиперсфера |
Число кластеров, степень нечеткости |
Центры кластеров, матрица принадлежности |
|
Иерархический |
Произвольная |
Число кластеров или порог расстояния для усечения иерархии |
Бинарное дерево кластеров |
|
Минимально покрывающего дерева |
Произвольная |
Число кластеров или порог расстояния для удаления ребер |
Древовидная структура кластеров |
|
Послойный |
Произвольная |
Последовательность порогов расстояния |
Древовидная структура кластеров с разными уровнями иерархии |
Рассмотрим, какие объекты в социальных сетях можно кластеризовать для успешной борьбы со спамом.
– Текстовые сообщения. Это наиболее очевидный объект, который можно кластеризовать, так как в социальных сетях текстовые сообщения используются в личных сообщениях, статусах, групповых публикациях, информации об аккаунте и т.д. Для кластеризации текстовых документов часто используют алгоритм k-means [4].
– Изображения. Со временем спамеры стали использовать «графический» спам, что значительно затрудняло анализ, но достаточно быстро появились ответные меры для борьбы с этим, в том числе распознавание текста с изображений [5]. Кластеризовать можно как сами изображения, группируя как полностью одинаковые изображения, так и схожие. Кроме того, при комбинировании кластеризации текста с распознаванием текста на изображениях становится возможным кластеризовать разные изображения на основе одинакового или схожего текста на них.
– Пользователи. Это ключевой элемент в любой спам-рассылке, так как без аккаунтов рассылка становится невозможной. Выделяют различные группы аккаунтов, которые могут быть использованы для рассылок спама. Сервисы обладают очень обширной информацией о существующих аккаунтах, что позволяет выделить множество атрибутов для последующей кластеризации пользователей.
Для кластеризации спама в социальных сетях подходит множество алгоритмов. Выбор конкретного алгоритма может зависеть от используемого стека технологий в конкретной социальной сети. Кроме того, наиболее важным для качественной кластеризации является подбор входных данных, то есть атрибутов, которые и будет необходимо кластеризовать, особенно это касается задачи кластеризации пользователей.
Другим не менее важным фактором является производительность алгоритма. Это действительно является важным параметром, так как объем контента и данных в социальных сетях очень большой.
Рассмотрим опыт применения кластеризации данных для борьбы со спамом и другим нежелательным контентом. Социальная сеть Badoo рассказала об использовании кластеризации текстовых сообщений с использование k-means [6]. Facebook для борьбы с дезинформацией, так называемыми фейковыми новостями, использует в том числе и кластеризацию [7]. Linkedin использует кластеризацию для задачи предотвращения злоупотреблений [8]. «Юла» проводит кластеризацию по каждой сущности объявления, чтобы найти дубликаты [9].



