Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Разработка производственных систем с искусственным интеллектом в нефтепереработке направлена на решение задач моделирования процессов оперативного управления, расчета показателей качества, управления технологическими процессами, разработки динамических баз данных и знаний [1]. Искусственные нейронные сети (ИНС) как составной компонент Industry 4.0 имеют огромный потенциал оптимизации производственных процессов и снижения затрат нефтеперерабатывающих заводов (НПЗ). Цифровые технологии позволяют улучшить управление производственным процессом на основе достоверной информации, повышают производительность труда.

Следует отметить, что планирование, составление расписаний и оптимизация смешения продукции производят ощутимый эффект [2–4], который можно существенно увеличить за счет ИНС [5, 6]. При этом прогноз качества продукции в нефтепереработке выступает как один из основных элементов практического приложения ИНС [5, 7].

Актуальным вопросом является моделирование низкотемпературных свойств дизельного топлива [5, 7, 8]. Во-первых, объем производства дизельного топлива в России максимальный среди других нефтепродуктов, и его выпуск поддерживается стабильным внешним и внутренним спросом. Во-вторых, климатические условия РФ вызывают большую потребность в высококачественных низкозастывающих дизельных топливах, которая удовлетворяется менее чем наполовину [9]. Эффективность нефтепереработки существенно вырастет, если математическое моделирование даст возможность вычислить низкотемпературные свойства дизельного топлива вместо проведения дорогостоящих физических измерений.

Основными параметрами, характеризующими низкотемпературные свойства, выступают температура помутнения и предельная температура фильтруемости (ПТФ). Если температура помутнения может быть вычислена с применением достаточно простой линейной регрессии, то расчет ПТФ требует построения сложных нелинейных моделей [7]. Вместе с тем ПТФ – это весьма важный показатель для потребителей, поскольку определяет минимальную температуру, при которой будет обеспечен бесперебойный поток в топливных системах [10]. В работах [7, 8] для некоторого заданного набора лабораторных данных отмечена приемлемая точность прогнозирования ПТФ с помощью ИНС. Тем не менее для ряда точек абсолютная погрешность остается высокой, и для практического применения ИНС требуются исследования, направленные на повышение точности прогнозирования.

Наиболее широкое распространение при анализе качества получили сети прямого распространения, такие как многослойный персептрон (МП) и сеть радиально-базисных функций (РБФ) [7, 8]. Они позволяют сравнить предсказанные моделью результаты с известными значениями зависимых переменных [11]. Нейросетевые модели не требуют формулировки гипотез о взаимосвязи между зависимыми и независимыми переменными, расчет происходит в процессе обучения. Хотя результаты моделирования ИНС представляют систему «черный ящик» и с трудом поддаются интерпретации, оценка важности значений предикторов позволяет анализировать зависимость выходной функции от входных переменных.

Целями работы являются разработка способов уменьшения погрешности прогнозирования качественных характеристик нефтепродуктов с помощью искусственных нейронных сетей на примере предельной температуры фильтруемости дизельного топлива; определение степени влияния входных параметров на итоговый прогноз.

Основные задачи могут быть сформулированы следующим образом: построение прогноза для определения ПТФ по другим известным физико-химическим параметрам; исследование влияния алгоритмов обучения, функций активации сетей и числа нейронов на точность прогнозирования; статистический анализ данных для выявления примеров, оказывающих отрицательное влияние на точность прогнозирования; оценка влияния предикторов на низкотемпературные свойства дизельного топлива.

Материалы и методы исследования

Для обучения ИНС использовались паспортные данные зимнего дизельного топлива, предусмотренные стандартами на готовую продукцию [12]. Входной слой включал 10 нейронов с показателями: цетановое число; цетановый индекс; плотность при 15 °С (кг/м3); массовая доля полициклических ароматических углеводородов ( %); массовая доля серы (мг/кг); температура вспышки в закрытом тигле ( °С); кинематическая вязкость при 40 °С (мм2/с); объем перегонки до 180 °С и до 360 °С ( % об.); температура выкипания 95 % объема ( °С). Поскольку изменение остальных характеристик было несущественным, то и в построении нейронной сети они не участвовали. На выходе имелся только один нейрон для расчета ПТФ ( °С).

Вычисления и статистическая обработка информации осуществлялись с помощью компьютерной программы SPSS Statistics. В процессе построения модели множество данных делилось случайным образом на обучающее, тестирующее и контрольное. Контрольное множество ни в обучении, ни в оптимизации и тестировании сети не участвовало. Результаты сравнения для контрольного множества являлись основным фактором при сравнении архитектуры сетей, функций активации и выбора методов решения.

Расчет ПТФ проведен для МП с различным числом скрытых слоев и сетей РБФ. Созданы нейросетевые модели для одной зависимой переменной на основании значений переменных предикторов. Многослойный персептрон включает входной слой, ряд скрытых слоев и выходной уровень. Для обучения сети варьировались алгоритмы, архитектура сети и число нейронов.

В отличие от многослойного персептрона, сеть РБФ включает только 3 уровня: входной, один скрытый и выходной. Функциями активации в скрытом слое являются радиальные базисные функции. Широкое применение нейронных сетей РБФ обусловлено простой структурой сети и высокой скоростью обучения.

Обозначим через Y множество значений ПТФ, G+, G– – граничные точки данного множества. При оценке результатов работы ИНС вычислялась средняя абсолютная погрешность MAE (Mean Absolute Error) по формуле:

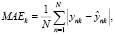(1)

где 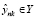– измеренное, ynk – прогнозируемое значение ПТФ для k-ой группы n-го значения, N – количество примеров. Следующим важным показателем, характеризующим работу сети, является средняя абсолютная процентная погрешность MAPE (Mean absolute percentage error)

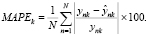(2)

Были проведены расчеты с разным числом нейронов. Определено оптимальное количество нейронов, которое обеспечивает наименьшую относительную погрешность для контрольных данных и наименьшие значения показателей (1) и (2).

В основе предлагаемой методологии лежит статистический анализ влияния исходного обучающего множества на точность прогноза. Известно, что в исходной информации могут быть данные, которые выпадают из общей закономерности. Их исключение приводит к уменьшению погрешности обучения сети и улучшению прогноза [11]. Проведено последовательное исключение примеров из обучающего множества и вычислена погрешность ИНС, обученной на таких усеченных множествах.

Результаты исследования и их обсуждение

На первом этапе исследования рассмотрено 188 примеров в диапазоне изменения ПТФ от –34 °С до –28 °С (Ряд 1 на рис. 1). Расчеты показали, что уменьшение аберрации прогнозируемых значений ПТФ происходит при исключении ряда примеров из обучающего множества. Для дальнейшего исследования были удалены примеры со значениями, принадлежащими нижней границе интервала 1,5*IQR (IQR – межквартильный размах). Они вносят наибольшие погрешности, и включать их для обучения ИНС нецелесообразно. С целью уменьшения погрешности прогнозирования ПТФ выбран измененный массив данных 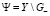, содержащий 180 точек (Ряд 2 на рис. 1). Отметим, что МП позволяет идентифицировать примеры, которые выпадают из закономерности, характерной для изучаемого массива данных.

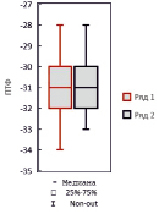
Рис. 1. Диаграмма ящик с усами исходного массива данных предельной температуры фильтруемости (ПТФ), обозначенных Ряд 1, и с исключенными примерами – Ряд 2

Обучающее множество для МП включало 102 (56,7 %) примера, тестовое – 23 (12,7 %) и контрольное – 55 (30,6 %). Расчет ПТФ с максимальной точностью обеспечивает нейронная сеть с 2 скрытыми слоями, 7 нейронов было задействовано на первом скрытом слое и 3 – на втором. Функция активации – гиперболический тангенс. При обучении применялся метод масштабируемых сопряженных градиентов.

Для сети РБФ обучающее множество содержало 104 (57,8 %) примера, тестовое – 35 (19,4 %) и контрольное – 41 (22,8 %). Лучшие результаты для контрольного множества обеспечила нормализованная радиальная базисная функция с 9 нейронами скрытого слоя.

Как МП, так и сети РБФ дают погрешности, которые находятся в пределах, предусмотренных национальным стандартом [10]. Расчет показателей (1) и (2) представлен в табл. 1, в которой K указывает номер модели, N – количество примеров, показатели MAE и MAPE вычислены по формулам (1), (2). Как следует из приведенной таблицы, МП c показателями МАЕ3 = 0,4 °С и МАРЕ3 = 1,3 % дает существенно лучшие результаты, чем сеть РБФ (табл. 1). Этот вывод совпадает с результатами, полученными в работе [8] для других входных данных и сети с другим числом нейронов. Многослойный персептрон для примеров, исключающих нижнюю границу интервала, отделяющего выбросы, имеет показатели в 2,5 раза меньшие (табл. 1). Таким образом, исключение 4 % точек из обучающего множества существенно улучшает прогноз.

Таблица 1

Сравнение статистических показателей для МП и сети РБФ

Для МП (табл. 1, К = 3) получены наилучшие результаты и обеспечено вычисление ПТФ с абсолютной погрешностью, соответствующей стандартам измерения [10]. На рис. 2 приведены исходные значения ПТФ и прогнозируемые значения, рассчитанные ИНС. Для приведенного в работе диапазона температур расхождение менее 2,0 °С, что соответствует стандарту по определению ПТФ [10].

Для МП осуществлен анализ чувствительности, при котором производилось вычисление важности каждого входного параметра ИНС на основе обучающих и проверочных примеров. В табл. 2 приведены данные, полученные с помощью МП, показывающие важность и нормализованную важность для каждого предиктора при расчете ПТФ.

Наиболее существенное влияние, как следует из табл. 2, оказали показатели объема перегонки до 360 °С и температуры выкипания 95 % объема. Информация представляет интерес при анализе производственных процессов и может служить основой для построения регрессионных моделей.

Заключение

Модель с применением ИНС способна обеспечить необходимую для промышленного применения точность, поскольку абсолютная погрешность вычисления ПТФ соответствует требованиям стандартов измерения.

Численные эксперименты показали, что уменьшение аберрации прогнозируемых значений базируется как на выборе оптимальных параметров модели, так и на статистическом анализе исходных данных. В задачах определения низкотемпературных свойств дизельных топлив МП дает лучшие результаты, чем сеть РБФ, и рекомендуется для применения. Исключение ряда примеров, принадлежащих одной из границ обучающего множества, существенно повышает точность прогноза.

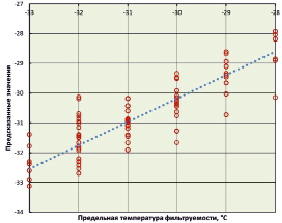
Рис. 2. Предсказанные и исходные значения предельной температуры фильтруемости зимнего дизельного топлива