В статье [1] представлены некоторые результаты по использованию общей памяти в криптографических протоколах, использующих симметричное шифрование, и, в частности, показано, что общую память отправителя и получателя можно использовать для противодействия MITM-атакам противника в канале связи. Метод применения общей памяти в криптографических протоколах сравнительно нов, поскольку выводит за пределы модели секретной связи К. Шеннона, и идеологию открытого распределения ключей. Однако использование ОП памяти не противоречит криптографической модели угроз Долева-Яо (1976 г.), в которой противник не имеет доступа к устройствам, принадлежащим отправителю и получателю. В работе [1] также отмечено, что общий подход использования общей памяти и соответствующие протоколы – нуждаются в проработке и детализации.
Воспроизведенный в [1] протокол создания симметричного ключа на основе предварительного здесь мы называем доверительным. Такой протокол в потенциале своего использования может оказаться слаб по отношению к Получателю – В-лгуну – участнику протокола, меняющего корректные данные протокола и заинтересованного в корректном завершении его работы. Кроме того, В-лгун может входить в сговор с противником в канале связи, становясь более опасным, чем сам противник. Для закрытия подобной слабости здесь мы приводим проверяемый ключевой протокол, по своей симметрии похожий на протокол Диффи – Хеллмана, встроенного в TLS протоколы [2]. Проверяемый протокол, в отличие от протокола Диффи – Хеллмана, не использует трудность дискретного логарифма, а основан на невозможности противника в канале связи получить доступ к значениям общей памяти.
Деревья Дамгарда – Меркла, которые находят широкое применение в качестве базовой основы криптовалют Bitcoin и Etherium [3] и контроля целостности больших массивов данных, мы используем для построения протоколов контроля целостности и удаленной синхронизации общей памяти.
Цель исследования: Разработка криптографического протокола передачи и создания ключа с использованием общей памяти у отправителя и получателя, а также транспортного протокола. Такой протокол планируются как альтернатива протоколу Диффи – Хеллмана и его использование в гибридных криптографических системах. Предложения по удаленному контролю целостности общей памяти на устройствах отправителя и получателя.
Общая память и определения
Повторим основные определения из предыдущей статьи [1] и работы [4], и для этого обозначим здесь и далее m > 1 размер симметричного криптографического ключа k,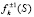 
функции симметричного шифрования/расшифрования и пусть Hk(S) – ключевая хэш-функция, сильно сопротивляющаяся поиску коллизий.
Определение 1. Назовем общей памятью Отправителя (A) и Получателя (В) – согласованное между Отправителем и Получателем и разнесенное на устройства Отправителя и Получателя числовое множество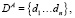 
n > 1, n < m. Верхний индекс X = {A,B} указывает, на каком устройстве располагается общая память.
Процедура создания общей памяти, выработки первого значения симметричного ключа и первого ключевого хэша не предполагает использования канала связи, и выполняется в момент создания множества D.
Определение 2. На основании общей памяти создадим предварительный ключ
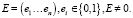(1)
Сеансовый ключ генерируется по формуле
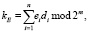(2)
где, напомним, m – размер сеансового ключа шифрования.
Утверждение 1. Пусть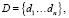 
n > 1, n < m – общая память, созданная на устройствах отправителя и получателя (DA = DB) в модели секретной связи К. Шеннона, E – предварительный ключ, kE – сеансовый ключ. Тогда противник С по значению предварительного ключа E ≠ 0 не может построить симметричный ключ kE. Это можно выразить в терминах условной энтропии К. Шеннона. H(S|Si): меры неопределенности значения S при условии обладания значением Si
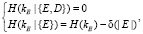(3)
где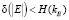 
.
Доказательство использует технику (2-2) пороговых схем разделения секрета, для которых секретным значением является ключ kE. Долями секрета являются соответственно значения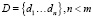 
, 
.
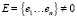В силу разбалансированности размеров долей секрета друг относительно друга, такая схема разделения секрета является неидеальной и несовершенной, но является пороговой. Из несовершенности вытекает, что противник С, перехватывая вектор E получает некоторую информацию δ о значении ключа, но недостаточную, чтобы уточнить его значение. Техника несовершенных и почти совершенных схем разделения секрета исследована, в частности, в [5].
В терминах условной энтропии К. Шеннона, понимаемой относительно вероятностных распределений для значений kE, E, D, первое равенство в (3.1) означает, что неопределенность значения ключа kE по значениям теней E, D полностью снимается. Второе соотношение, важное для противника С в канале связи, определяет меру неопределенности симметричного ключа для противника С при перехвате предварительного ключа.
Точную оценку δ в терминах формул воспроизвести достаточно сложно, так как значения общей памяти заранее не определены. Но мы можем указать максимально возможное значение δ = 1. Для этого нами построены примеры. Пусть Е – множество предварительных ключей, K – множество сеансовых ключей, которые можно получить с использованием формулы (2). Очевидно, мощность множества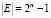 
,
а множества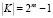 
, здесь исключен случай нулевого вектора. В построенных нами примерах пересечением множеств предварительных и сеансовых ключей является пустое множество.
E ∩ K = Ø. (4)
Отметим, что согласно принципу Керхгоффса в криптографии, противник сможет знать и формулу (4). Это дает ему информацию о множестве сеансовых ключей, так что при брутфорсинге симметричных ключей он может отбросить случаи ключей из интервала [1; 2m] и проводить атаку на ключи на множестве [2n + 1; 2m].
Далее, пусть распределение значений симметричных ключей из множества K – равномерно и равновероятно на [2n + 1; 2m]. В этом случае, хорошо известно, энтропийные оценки (3) принимают максимальные значения, в которых вместо условной энтропии участвует мера Хартли. Грубые оценки мер Хартли для множеств [1; 2m] и [2n + 1; 2m] дают неравенство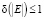 
, где случай равенства достигается для случая n = m – 1. Это завершает доказательство утверждения 1.
Из утверждения 1 следует, что неопределенность значения симметричного ключа для противника С при перехвате предварительного ключа E снимается не более чем на один бит. В работе [6] описывается лгун в схемах разделения секрета.
Доверительный ключевой и транспортный протоколы
Доверительные протоколы создания симметричного ключа и передачи сообщения уже были предложены в статье [1]. Эти протоколы мы назвали доверительными, за счет того, что одна из сторон обмена сообщениями Отправитель А или Получатель В всецело доверяет противоположной стороне. Кто-либо из них может подменить данные при передаче сообщения. В протоколе (5) все проверки, и заключение об успешности завершения работы протокола происходят на стороне Получателя В, так что он в потенциале может быть лгуном.
Доверительный протокол создания симметричного ключа безопасный по отношению к противнику в канале связи:
1. 
.
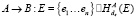2. В: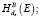 
если 
,
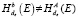то стоп.
3. 
.
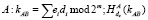4. 
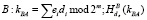. (5)
5. 
.
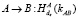6. В: если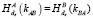 
, то de ← kВА,
иначе стоп.
7. 
.
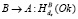8. A: если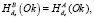 
то de ← kAВ.
Доверительный протокол обмена сообщениями:
1. 
.
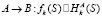2. 
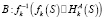. (6)
3. B: если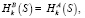 
то Ok.
При корректном завершении работы протокола и равенстве значений хеш-функций на шаге (6.3), сообщение S считаем успешно переданным.
Протоколы (5), (6) эффективно противостоят MITM-атаке за счет использования ключевой хэш-функции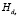 
с ключом de – предыдущим сгенерированным сеансовым ключом. Активный противник, вмешиваясь в процесс передачи сообщений, может лишь портить пересылаемые данные, при этом Отправитель и Получатель на этапах (5.6) и (6.3) определят факт подмены сообщения.
Протокол (6) назовем транспортным протоколом, а фраза ТРАНСП(S) означает передачу сообщения S с помощью этого протокола.
Проверяемый ключевой протокол
Определение 3. Лгуном в протоколе называем законного участника протокола, заинтересованного в подмене данных в рамках действия протокола и корректном завершении работы протокола. Протоколы с лгунами естественным образом возникают в протоколах схем разделения секрета и впервые рассматривались в работе [7].
В предыдущих протоколах предполагается, что отправитель А выступает в роли «дилера» ключа, так как он генерирует предварительный ключ. В свою очередь получатель В осуществляет все сравнения хэш-значений в протоколах и ему же принадлежит роль определения корректности завершения работы протоколов (5), (6). Роли А и В в протоколах неравноправны и основаны на значительном доверии А к В и соответственно В к А. Поэтому представленные выше протоколы мы можем назвать доверительными. В отличие от противника С, В-лгун имеет доступ к общей памяти D, что позволяет ему строить ключ kBA = kAB, а также знает ключ de и может получить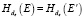 
. Для противодействия В-лгуну необходимы усиления приведенных протоколов в виде двусторонних проверок передаваемой информации. Этим достигается определенная симметрия доверия А и В так, как это происходит в протоколе Диффи – Хеллмана:
1. 
.
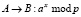2. 
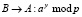. (7)
3. 
.
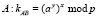4. 
.
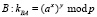Как можно заметить, в (7) протоколе доверие между А и В критично, и в случае обмана одного из участников обмена сообщениями, общий ключ на шаге 4 корректно выработан не будет Протокол в определенном смысле симметричен по отношению доверительности участников протокола.
Обозначим ⊕ – оператор поразрядного сложения исключающего ИЛИ. Приведем проверяемый протокол, аналог протокола (7), устойчивый к атакам В-лгуна:
1. 
.
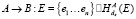2. B: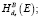 
если 
,
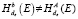то стоп.
3. 
.
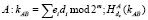4. 
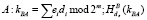. (8)
5. 
.
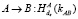6. B: если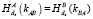 
, то OK1, иначе стоп.
7. 
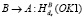. (9)
8. A: Если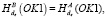 
то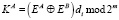 
, иначе стоп.
9. A: запрашивает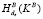 
.
10. 
.
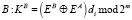11. 
.
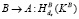12. A: Если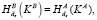 
то de ← kBA, иначе стоп.
13. 
.
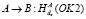14. A: Если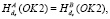 
то de ← kBA, иначе стоп.
Утверждение 2. Пусть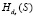 
сильно сопротивляется поиску коллизий, тогда в проверяемом ключевом протоколе ни А, ни В не могут быть лгунами без их обнаружения на другой стороне.
Динамическая общая память.
Контроль целостности общей памяти
Обозначим дерево Дамгарда – Меркла DMX, построенное над общей памятью соответственно Отправителя для X = A и Получателя для X = B. Свойства этих деревьев хорошо известны и использованы в работе [1] для определения целостности общей памяти на устройствах А и В.
Ввиду изменения общей памяти за счет динамической компоненты становится особенно важно поддерживать целостность памяти. Контролировать общую память предлагается с использованием техники построения деревьев Дамгарда – Меркла. В таких деревьях корневой хэш Root_Hash представляет из себя результат попарной конкатенации всех вершин дерева. Очевидно, что, при совпадении корневых хэшей двух деревьев – совпадает и их общая память.
Для контроля целостности общей памяти Отправителя и Получателя предлагается использовать следующий протокол:
1. B: запрашивает Root_Hash(A).
2. A → B: ТРАНСП (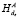
(Root_Hash(A)).
3. B: сравнивает полученный Root_Hash(A) со своим Root_Hash(B). (10)
3.1. B: если Root_Hash(A) = Root_Hash(B),
то OK (Shared_Memory(A) = Shared_Memory(B));
3.2. B: если Root_Hash(A) ≠ Root_Hash(B), то применяем ДОКАЗАТЕЛЬСТВО_МЕРКЛА (Shared_Memory(A) ≠ Shared_Memory(B)).
Протокол либо успешно завершает работу на этапе (3.1), когда корневые хэши Отправителя и Получателя равны, а значит и общая память в целом у них совпадает, либо на этапе (3.2) запускаем протокол доказательства Меркла, так как корневые хэши не совпадают, следовательно, общая память у Отправителя и Получателя различна.
ДОКАЗАТЕЛЬСТВО_МЕРКЛА:
1. B запрашивает хэши всех элементов общей памяти.
2. A → B: ТРАНСП (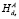
(Shared_Memory(A)[i])).
3. B: сравнивает полученный хэш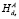 
(Shared_Memory(A)[i]) со своим 
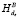(Shared_Memory(A)[i]). (11)
3.1. B: если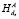 
(Shared_Memory(A)[i]) =
= 
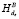(Shared_Memory(A)[i]), то обращаемся к следующему элементу общей памяти;
3.2. B: если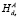 
(Shared_Memory(A [i]) ≠
≠ 
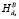(Shared_Memory(A)[i]) зануляем бит в предварительном ключе, соответствующий несовпадающему элементу памяти.
Проигрывание протоколов (10), (11) позволяет удаленно синхронизировать общую память на устройствах А и B. Сначала применяется протокол, который дает понять, нарушена ли целостность памяти (10). Если не нарушена – то достаточно только применения протокола (10), в противном случае – после протокола (10) применяем протокол (11) для игнорирования несовпадающих элементов общей памяти предварительным ключом, зануляя соответствующую компоненту предварительного ключа.
Динамическая общая память
В статье [1] указано, что противник С, постоянно вмешиваясь в проигрывание ключевых, может разрушать их работу, вызывая оператор стоп. Использование динамической компоненты в общей памяти, представленной в виде очереди, во многом может снять трудности выполнения протоколов. Динамическое изменение общей памяти зададим преобразованием
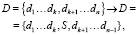(12)
где di – элемент общей памяти;
S – успешно переданное последнее сообщение.
Пример использования динамической общей памяти, позволяющий порождать новый сеансовый ключ, без проигрывания ключевых протоколов.
Пусть размер симметричного ключа шифрования m = 128. Количество элементов общей памяти n = 40.
Общая память D = {80, 65, 33, 86, 35, 22, 49, 95, 86, 33, 25, 80, 27, 68, 8, 44, 69, 28, 65, 21, 91, 2, 34, 74, 74, 35, 67, 1, 37, 72, 8, 93, 66, 43, 60, 66, 14, 15, 36, 60}.
В данном примере первые 30 элементов (d1…d30) общей памяти постоянны и в статье [1] эту область памяти мы назвали статической компонентой, а последние
10 ({d31…d40} или {8, 93, 66, 43, 60, 66, 14, 15, 36, 60}) – динамической компонентой, имеющей структуру – очередь.
Предварительный ключ E = 1011000101111001011011011100001010100110. Получим сеансовый ключ на основании имеющихся данных по формуле (2): k = 1057.
Передадим с использованием транспортного протокола сообщение S = «101» и изменим общую память согласно (12). Динамическая компонента принимает следующий вид: {101, 8, 93, 66, 43, 60, 66, 14, 15, 36}.
Структура общей памяти изменится в соответствии с формулой (12).
Измененная общая память D' = {80, 65, 33, 86, 35, 22, 49, 95, 86, 33, 25, 80, 27, 68, 8, 44, 69, 28, 65, 21, 91, 2, 34, 74, 74, 35, 67, 1, 37, 72, 101, 8, 93, 66, 43, 60, 66, 14, 15, 36}.
Таким образом, у нас изменилась общая память, предварительный ключ остался прежним, следовательно, и мы имеем согласованное изменение значений сеансового ключа (2): k = 1138 на устройствах Отправителя и Получателя.
Заключение
Среди предложенных протоколов генерации симметричного ключа, конечно, желательно применять протокол (9) вместо (5), так как в нем происходит двусторонняя проверка между отправителем и получателем. Это позволяет обезопасить обмен сообщениями от лгуна – участника протокола, при двусторонней проверке он будет вычислен.
Использование динамической общей памяти (12) снимает одну из традиционных и трудных проблем симметричной криптографии – безопасную передачу и/или создание симметричного ключа по двустороннему криптографическому протоколу, заменяя проблему передачи/создания синхронным преобразованием общей памяти на двух устройствах. Однако здесь возникает следующая важная задача – постоянное поддержание целостности общей памяти на устройствах Отправителя и Получателя, для чего предлагается использовать протоколы (10), (11).
Благодаря протоколам (10), (11) мы можем удаленно контролировать общую память у Отправителя А и Получателя В. Протокол (10) позволяет определить, совпадает ли общая память на устройствах А и В, а протокол (11) – избавиться от несовпадающих элементов при создании предварительного ключа.
Работа выполнена при поддержке и финансировании Российского фонда фундаментальных исследований, грант № 18-01-00596А.