Оценка цифровых снимков дистанционного зондирования Земли (ДЗЗ), доставляемых средствами технического зрения с различными оптико-физическими свойствами, позволяет выполнять объективный отбор изображений, пригодных для дальнейшей интерпретации: выделения и распознавания целевых объектов. Большое количество разных видов дефектов качества, а также сложность структур самих изображений вынуждает использовать различные методы оценок качества или их комбинации. Некоторые методы очень сложны из-за большого количества одновременно используемых метрик. На сегодняшний день разработано большое количество методов оценки качества изображений. Эти методы можно классифицировать:
- по способу оценки: сравнительные (сравнение с эталоном) и абсолютные (оцениваются параметры самого изображения);
- по объективности оценок: количественные (формализованные) методы оценки качества и субъективные (экспертные) методы оценки.
Оценки, полученные разными методами, могут противоречить друг другу [1], но в целом каждая из них обладает определенными особенностями, которые свойственны зрительной системе человека. Известные экспертные оценки, описанные, например, в стандарте «Recommendation ITU-R BT.500-11» [2], весьма трудоемки. Они практически неприменимы для непрерывной обработки большого количества изображений за короткое время, что имеет место в системах анализа потоков снимков ДЗЗ.
Перечислим некоторые меры и методы количественной оценки качества растровых изображений [1, 3, 4]:
- среднеквадратичное отклонение (СКО, англ. Standard Deviation), используется для определения количественной разницы пикселей искаженного изображения и образца;
- пиковое отношение сигнала к шуму (ПОСШ, англ. Peak Signal-to-Noise Ratio) – соотношение между максимумом возможного значения сигнала и мощностью шума, искажающего сигнал;
- мера структурного подобия (МСП, англ. Structure Similarity), основывается на том, что пространственно близкие пиксели имеют сильную взаимосвязь, несущую важную информацию о структуре объектов и о сцене в целом;
- метод CRI (коэффициент восстановимости изображения, англ. Coefficient of Recoverability Image) не требует наличия образца и имеет хорошую устойчивость к шумам и искажениям контраста;
- метод PQS (шкала качества изображения, англ. Picture Quality Scale) требует наличия образца; использует пять разных оценок на каждый из факторов, оказывающих влияние на качество изображения;
- модифицированный метод структурного подобия (англ. Multi-Scale Structural Similarity, MS-SSIM) отличается тем, что изображение многократно масштабируется, параметры качества оцениваются на изображениях разного масштаба, результирующая оценка получается объединением измерений в разных масштабах;
- метод IQI (англ. Image Quality Index) рассчитывает степень искажений по трем факторам: корреляция, искажение яркости и контраста.
Следует отметить, что перечисленные меры и методы существенно зависят от особенностей конкретных изображений и отдельных измеряемых факторов, что затрудняет оценку качества снимков ДЗЗ.
Цель исследования: разработка метода, позволяющего оценивать качество изображений ДЗЗ при отсутствии эталонных образцов. В настоящей работе для этого предлагается использовать искусственную нейронную сеть (ИНС) прямого распространения, обучаемую с учителем на оригинальных и искусственно поврежденных изображениях.
Материалы и методы исследования
Для оценки изображений без образцов могут применяться методы искусственного интеллекта, в том числе аппарат ИНС. Например, в работе [5] описан метод оценки качества изображений без использования эталонных образцов, основанный на глубоких сверточных нейронных сетях. Представленные сети получают необработанные части изображений (image patches) на вход и оценивают качество без использования знания о других областях. В отличие от работы [5], нами предлагается использовать искусственную сеть прямого распространения, обучаемую специальным образом, о чем далее будет сказано подробнее.
Для подготовки обучающей выборки и дальнейших экспериментов был использован архив снимков ДЗЗ, полученных с борта Международной космической станции (МКС) [6]. Все изображения были уменьшены в четыре раза, а затем интерполированы (увеличены) с разным качеством методом ближайшего соседа (Nearest Neighbored) и бикубическим методом (Bicubic). Указанные методы были выбраны, так как они вносят искажения разного характера [4].
В случае метода ближайшего соседа пикселям нового изображения присваиваются значения ближайшего пикселя из исходного изображения. Метод сохраняет острые границы изображений, но вносит ступенчатый эффект; имеет минимальное потребление вычислительных ресурсов. При бикубической интерполяции значения цвета новых пикселей вычисляются на основе функции интерполяции значений цветов близких 16 пикселей исходного изображения (в пределах прямоугольной области 4x4 пикселя). Метод обеспечивает лучшую передачу гладких контуров объектов, но может приводить к усилению шума или пропаже мелких деталей. Применение этих методов способно снижать резкость границ на изображениях, в том числе приводить к «лестничному эффекту». Кроме того, на качество изображения может повлиять применяемый способ хранения и передачи: сжатие с потерями, ограничение разрядов яркости (8, 24-битные изображения) и т.п. На цифровых фотографиях изначально присутствуют некоторые дефекты качества: небольшой шум (разница в яркости пикселей, обычно в пределах 1–2 единиц целочисленного значения градаций яркости), расфокусировка и другие дефекты, вызванные физическими характеристиками устройств и условиями фотосъемки.
В обучающую выборку включены и некоторые изображения без искажений как образцы с высоким качеством. Примеры исходных изображений приведены на рис. 1.
Обрабатываемые изображения (оригинальные и искусственно поврежденные) попарно разбивались на фрагменты (окна) размером 16x16 пикселей без перекрытия. Размер окна влияет на точность оценок, требуемые вычислительные ресурсы и определяется экспериментально. Значения пикселей из обрабатываемого окна подаются на первый слой сети прямого распространения, имеющей сигмоидальную функцию активации, в виде вектора размером 256 (по числу пикселей в окне). Выбрана следующая структура двухслойной ИНС: первый слой – 130 нейронов, второй слой – четыре нейрона для оценки качества (плохое, среднее, хорошее, отличное).




Рис. 1. Изображения дистанционного зондирования Земли
Таблица 1
Соответствие СКО классам качества
|
Диапазон СКО |
Наименование класса качества |
Бинарный подход |
Нечеткий подход |
|
≥0.126 |
Плохое |
<1.0; 0.0; 0.0; 0.0> |
<1.0; 0.25; 0.0; 0.0> |
|
[0.006; 0.126) |
Среднее |
<0.0; 1.0; 0.0; 0.0> |
<0.25; 1.0; 0.25; 0.0> |
|
[0.0001; 0.006) |
Хорошее |
<0.0; 0.0; 1.0; 0.0> |
<0.0; 0.25; 1.0; 0.25> |
|
<0.0001 |
Отличное |
<0.0; 0.0; 0.0; 1.0> |
<0.0; 0.0; 0.25; 1.0> |
Для установки эталонных значений выходных сигналов использовались два подхода: бинарный и подход, опирающийся на нечеткую логику [7]. Всего было проведено четыре эксперимента, отличающихся способом интерполирования и, соответственно, способом формирования выходного сигнала. На анализируемых изображениях СКО лежали в диапазоне 0.00005–0.186 при среднем значении 0.066. В случае применения нечеткой логики параметры функций принадлежности устанавливались с перекрытием. Выбранные функции принадлежности нечеткой логики хорошо описывают связь между порядковыми дискретными величинами (классами качества): близкие по значению величины объединены соответствующей функцией принадлежности (см. табл. 1, описывающую классы качества).
Для настройки ИНС в соответствии с предложениями работы [8] использовалась случайная 20 %-ная учебная выборка из общего числа извлеченных фрагментов изображений.
Результаты исследования и их обсуждение
ИНС с предложенной архитектурой удалось успешно обучить методом обратного распространения ошибки, в качестве фитнес-функции при этом была использована средняя квадратичная ошибка выходного вектора. Норма обучения установлена равной 0.1, поскольку при большем значении сеть не давала ожидаемых результатов (переобучалась). ИНС обучалась на протяжении 100 эпох, в каждой эпохе использовался 1 млн случайно выбранных фрагментов изображений. Уровень ошибки сети на 1, 10, 20, 50 и 100-й эпохах представлен в табл. 2.
Таблица 2
Результаты настройки ИНС в зависимости от числа эпох
|
Количество эпох настройки ИНС |
|||||
|
1 |
10 |
20 |
50 |
100 |
|
|
Бинарный вектор |
0,28 |
0,22 |
0,16 |
0,16 |
0,15 |
|
Бинарный вектор |
0,28 |
0,22 |
0,19 |
0,16 |
0,14 |
|
Нечеткая логика |
0,18 |
0,12 |
0,11 |
0,10 |
0,09 |
|
Нечеткая логика |
0,19 |
0,13 |
0,11 |
0,10 |
0,09 |
Из табл. 2 видно, что нейронная сеть, использующая бинарные эталонные вектора, имеет большую ошибку, чем ИНС с применением эталонных векторов на основе функций принадлежности.
Для визуализации результатов работы ИНС был разработан модуль формирования «тепловых карт» [9]. На рис. 2 приведен пример построенной тепловой карты для снимка города с борта МКС, интерполированного методом ближайшего соседа.
Белому цвету соответствует минимальное значение оценки ИНС, а черному – максимальное. Тепловая карта может быть использована для визуального контроля качества работы бортовой аппаратуры технического зрения. Блок-схема алгоритма формирования тепловых карт представлена на рис. 3.
В табл. 3 представлены корреляционные данные по некоторым из проведенных экспериментов, сопоставлялись результаты, полученные методом СКО и методом с применением ИНС.
Значения получены по формуле ранговой корреляции Спирмена для порядковых номеров классов качества непересекающихся фрагментов обрабатываемых снимков.
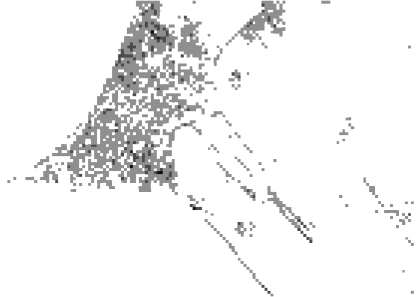
Рис. 2. Тепловая карта
Таблица 3
Корреляция результатов методов
|
Исходные данные |
Корреляция с оценкой СКО |
|
Изображение 2 (из обучающей выборки) |
0,59 |
|
Изображение 3 (из обучающей выборки, размытие Гаусса в GIMP) |
0,77 |
|
Изображение 4 (из обучающей выборки, размытие Гаусса в GIMP) |
0,76 |
|
Изображение 2707991195.jpg (из обучающей выборки, интерполяция методом ближайшего соседа) |
–0,75 |
|
Изображение 2707991195.jpg (эталон сам с собой) |
0,97 |
|
Изображение 7 (эталон сам с собой) |
0,94 |
|
Изображение 1353403202_bicub.png (бикубическая интерполяция, сравнивался сам с собой) |
0,77 |
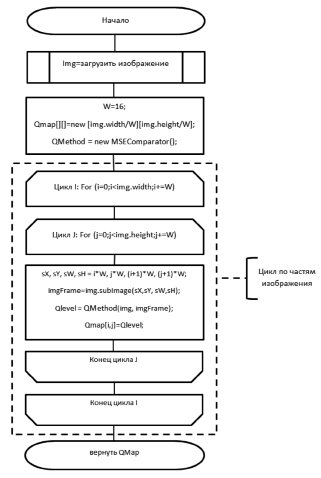
Рис. 3. Блок-схема алгоритма формирования тепловых карт
Заключение
Предложенный метод оценки качества изображений не требует наличия эталонного образца для сравнения и устойчив к изменениям набора снимков. ИНС позволяет получать результаты, близкие к оценке методом СКО. Показано, что применение методов нечеткой логики при подготовке эталонных векторов приводит к уменьшению ошибки сети. Метод требует относительно длительного предварительного обучения на подготовленных образцах, но позволяет проводить дообучение ИНС на новых выборках без изменения программного обеспечения.
Работа выполнена при финансовой поддержке Программы фундаментальных исследований Президиума РАН «Перспективные физико-химические технологии специального назначения» (проект «Разработка и исследование методов и технологии высокопроизводительного сжатия целевой информации, передаваемой по каналам космической связи в интересах национальной безопасности Российской Федерации»).



