В сложных технических системах в процессе эксплуатации возникают различные неисправности, в том числе связанные с выработкой ресурса и превышением допускаемых нагрузок. На металлургическом предприятии большое количество устройств и механизмов, которые включают в себя множество элементов. Такие системы будем называть сложными техническими системами. К ним относятся металлургические мостовые краны, несущие металлоконструкции которых испытывают тяжелые и весьма тяжелые режимы работы, быстро изнашиваются и переходят в аварийное состояние [1, 2].
Такая эксплуатация приводит к авариям и катастрофам. На сегодняшний день известны и совершенствуются методики расчета ущерба от эксплуатации различных технических систем [3, 4]. Актуальной является задача расчета ущерба от эксплуатации определенной группы технических систем на временном интервале, а также задания таких характеристик к ним, при которых средний ущерб от аварий стремился бы к минимуму.
Цель исследования: определить методику расчета возможного ущерба с целью ее использования для управления риском и безопасностью изучаемых технических систем.
Целью данной статьи является количественный модельный анализ характеристик ущерба совокупности несущих конструкций металлургических мостовых кранов, используя известные методики [3, 4].
Материалы и методы исследования
На металлургическом предприятии эксплуатируются около 1200 кранов различного назначения (по данным ПАО «Магнитогорский металлургичекий комбинат»). Характеристики их безаварийной эксплуатации и надежности изменяются как случайным так и закономерным образом.
Более половины кранов составляют металлургические мостовые краны, примем их количество 750. Предполагаем, что 750 кранов эксплуатировалась без превышения допустимых нагрузок в течение пятнадцати лет – гарантийный срок эксплуатации [3, 4].
К сожалению, на практике это почти невозможно, потму что, как правило, рассматриваемые краны работают в тяжелых и сверхтяжелых режимах. Конечно, при этом присутствуют аварии того или иного типа.
Тогда случайное событие возникновения аварии j-го типа Aj представляется дискретной величиной, принимающей значения 0 или 1 и характеризуемой вероятностью аварии P(Aj) = Pj [3, 4]. Ущерб U от нее представляется случайной непрерывной величиной Gj(Gj = Uj), полагая, что любой ущерб можно выразить в одинаковых единицах (условных относительных единицах).
Случайная величина безусловного ущерба Cj от аварии j-го типа, учитывающая факт отсутствия или возникновения аварии или величину ущерба, представляется в следующем виде:
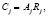(1)
Rj – характеристика риска.
Если произошла остановка работы конструкции крана, то ущерб может быть различным, но его величина характерна для данного типа аварии и не связана с вероятностью аварии. Риск будем рассматривать как математическое ожидание безусловного ущерба от аварии j-го типа.
Учитывая независимость случайных величин A и R, запишем выражение для дисперсии случайной величины C [3, 4]:
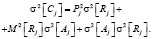(2)
Величины C случайны, зависимы и имеют положительную корреляцию. Возникновение аварии одного типа может перерастать в возникновение более тяжелой аварии.
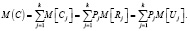(3)
Если ковариационная матрица бывает известна, то среднее квадратическое отклонение суммарного ущерба определяется зависимостью
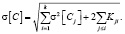(4)
Если же ковариационная матрица неизвестна, то, учитывая их положительное значение, можно найти границу величины дисперсии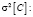 
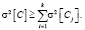(5)
Когда введены исходные данные, то есть определена группа сложных технических систем, работающих в одно и то же время, в одинаковых условиях, можно предположить, что их эксплуатация и режимы работы могут привести к трем типам аварий.
Будем различать следующие типы аварий:
– первый – аварии, не приводящие к остановке крана, или аварии, которые могут быть устранены без существенных изменений производственного цикла;
– второй – аварии, приводящие к остановке крана, производственного цикла и его ремонту;
– третий – катастрофические аварии, повлекшие за собой разрушение конструкции и гибель людей, остановку производственного процесса.
Очевидно, такая классификация достаточно условна, так как каждый тип аварии может появиться в любое время эксплуатации. Однако предполагаем, что первый тип аварии будет присущ первым годам эксплуатации крана, а второй и третий – годам выработки ресурса.
Будем также предполагать, что известны вероятности таких типов аварий, средние квадратические отклонения σ[Aj], математические ожидания M[Rj] и средние квадратические отклонения σ[Rj] случайного ущерба за год. Необходимо найти математическое ожидание суммарного ущерба за следующий год эксплуатации совокупности металлургических мостовых кранов и нижнюю границу дисперсии случайного суммарного ущерба.
Результаты исследования и их обсуждение
Приведем модельный пример расчета суммарного ущерба. Используя обработанные и известные данные по статистическим данным аварийности металлургических производств [4–6], представим в условных единицах исходные данные в табл. 1.
Таблица 1
Исходные данные по относительным единицам ущербов
|
j |
1 |
2 |
3 |
|
p |
0,1 |
0,01 |
0,0001 |
|
σ[Aj] |
0,01 |
0,001 |
0,00001 |
|
M[Rj], усл.ед. |
10 |
100 |
1000 |
|
σ[Rj], усл. ед. |
1 |
10 |
100 |
M[C1] = 0,1*10 = 1 усл. единица;
M[C2] = 0,01*100 = 1 усл. единица;
M[C3] = 0,0001*1000=0,1 усл. единица.
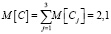усл. единица.
По (2) получим
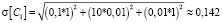усл. единиц;
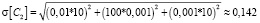усл. единиц;
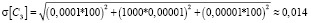усл. единиц.
На основании (5) получена нижняя граница среднего квадратичного отклонения суммарного ущерба
σ[C] ≥ 0,201 усл. единиц.
Интерпретировать полученные расчетные данные можно следующим образом. При анализе 750 рассматриваемых несущих конструкций металлургических мостовых кранов с подобными полученными характеристиками, становится очевидно что за пятнадцать лет их эксплуатации в таких же режимах без изменения показателей суммарный средний ущерб от возможных аварий составит 750 *15*2,1 = 23625 усл. единиц.
Таким образом, для группы металлургических мостовых кранов могут быть рассчитаны математические ожидания ущерба для всех рассматриваемых типов аварий.
Так, рассчитанный суммарный средний ущерб аварий первого типа M[Rj] = 10 будет соответствовать 2363 авариям, суммарный средний ущерб аварий второго типа M[Rj] = 100 будет соответствовать 236 авариям, суммарный средний ущерб аварий третьего типа M[Rj] = 1000 будет соответствовать 24 авариям за пятнадцать лет эксплуатации (рис. 1).
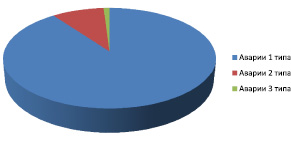
Рис. 1. Количество аварий конструкций кранов
Полученные расчетные данные удовлетворительно согласуются с реальными [6].
Одной из прямых характеристик ущерба является коэффициент смертельного травматизма на 1000 единиц техники. В табл. 2 и на рис. 2 приведены данные Ростехнадзора [6] за 2016 г.
Таблица 2
Коэффициенты опасности за 2016 г.
|
Вид техники |
Количество зарегистрированной техники |
Количество погибших |
Коэффициент смертельного травматизма |
|
Башенные краны |
17 403 |
10 |
0,57 |
|
Автомобильные краны |
61 875 |
6 |
0,10 |
|
Мостовые краны |
71 648 |
7 |
0,10 |
|
Козловые краны |
13 254 |
3 |
0,23 |
|
Гусеничные краны |
9 294 |
0 |
0 |
|
Краны-манипуляторы |
12 413 |
1 |
0,08 |
|
Портальные краны |
3 023 |
0 |
0 |
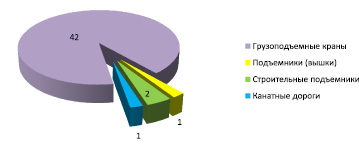
Рис. 2. Распределение аварий по видам техники (2016 г.)
Большее количество аварий и травматизма связано с эксплуатацией различных кранов, в том числе мостовых. Это обстоятельство лишний раз подчеркивает актуальность и правильность такого подхода, даже модельного.
Модельный расчет показывает, как важно рассчитать и учитывать риск аварий и ущерб от него таких потенциально опасных объектов, как несущие конструкции металлургических мостовых кранов. Такой подход позволяет связывать дальнейшую эксплуатацию рассматриваемых конструкций с оценкой их фактического состояния, с одной стороны, и уровнем безопасности, с другой, что важно при принятии различных управленческих решений.
Можно уменьшить вероятности аварий, если затратить на это дополнительные ресурсы или увеличить вероятность, сэконономив на стоимости производства и эксплуатации. Аналогично, затратив дополнительные ресурсы, можно уменьшить ущерб или, упростив конструкцию, можно увеличить средний ущерб от возможных аварий [3, 4].
Такая задача решается методом линейного программирования [7]. В самом простом случае его суть можно описать следующим: если уменьшение ущерба и вероятности аварии обойдется дешево, то можно максимально уменьшить эти характеристики и, наоборот, оптимальные значения требуют их увеличения.
Выводы
На предприятия металлургии в течение длительного времени поставляются грузоподъемные мостовые краны различного назначения. Они эксплуатируются в тяжелых и сверхтяжелых режимах работы. Это приводит к остановкам кранов, их незапланированным ремонтам, а в некоторых случаях, к серьезным авариям и гибели людей.
Оценка характеристик ущерба несущих конструкций металлургических мостовых кранов и других сложных технических систем представляет собой актуальную задачу.
Модельный расчет был основан на известных методиках, применяемых для расчета ущерба различных технических систем, обработанных данных Ростехнадзора и известных данных.
Величина ущерба от таких аварий случайна, но зависит не от факта, а от типа аварий. Возникновение аварии одного типа може породить более сложную и тяжелую.
Математическое ожидание суммарного ущерба и нижняя граница его среднего квадратического отклонения позволяют рассчитать суммарный ущерб от аварий различных типов. Такая методика позволяет в дальнейшем выявить оптимальное значение вероятности для каждого типа аварии и математическое ожидание ущерба от нее.
Приведенные расчеты позволяют задавать оптимальные требования к характеристикам рисков и безопасности как рассматриваемых технических систем, так и других типов сложных технических систем металлургического предприятия.
Приведенный модельный анализ доказывает правильность предпринятых ранее попыток расчета ущерба сложных технических систем и дополняет их. Кроме этого, расчетные материалы развивают теорию конструкционного риск-анализа и позволят в дальнейшем принимать верные инженерные управленческие решения.