Образовательная программа регламентирует, какой вид компетенции должен быть сформирован у студента при изучении той или иной дисциплины. Набор этих компетенций обусловлен конечным результатом подготовки выпускников. Бакалавр архитектуры, например, должен «владеть культурой мышления», «обладать способностью использовать воображение», «мыслить творчески», «анализировать проблемы и процессы», «моделировать исследования» [1]. Для формирования этих компетенций необходимо прежде всего иметь хорошо развитое как логическое, так и творческое мышление. Каждое из них имеет свою функциональную направленность.
Логическое мышление включает в себя умение разбить проблему на простейшие этапы и решать её пошагово путём выстраивания логических цепочек перехода от одного этапа к другому. Такое мышление можно назвать аналитическим, так как оно требует анализа ситуации, без которого нельзя выполнить поэтапную разбивку. При решении проблемы чаще всего используются известные разработки. Логическое мышление является абстрактным.
Творческое мышление включает в себя умение фантазировать и предлагать свои варианты решения проблемы, не обращая внимания на имеющиеся каноны. Творческий человек действует на уровне интуиции. Он не делит проблему на части, а рассматривает её в целом, т.е. синтезирует «целостный образ во всей совокупности его конкретных проявлений» [2]. Такое мышление является пространственным.
Многолетние наблюдения за студентами бакалавриата направлений подготовки «Архитектура и изобразительное искусство», а также школьниками 10–11 кл., решившими посвятить себя архитектуре, в процессе их обучения показывают, что:
- на вопрос анкеты «Доступно ли излагался материал?» все студенты отвечают «да», однако с заданием на закрепление этого материала самостоятельно справляются не все;
- студенты неудачно выступают на олимпиаде по начертательной геометрии, однако становятся победителями творческих конкурсов по архитектуре и рисунку, и наоборот, победители олимпиад либо не участвуют в конкурсах, либо не добиваются в них успеха;
- у большинства студентов затруднение вызывают позиционные задачи на пересечение прямой линии с плоскостью и пересечение двух плоскостей, но они с лёгкостью решают задачи на построение аксонометрии и перспективы;
- выполнять задание по проекционному черчению одни школьники начинают с построения проекций, другие – с аксонометрии.
Во всех случаях возникает вопрос: «Почему?»
Целью настоящего исследования является выяснение причины, казалось бы, противоречивых фактов и разработка возможных путей увеличения результативности образования на примере графических дисциплин.
В экспериментальном исследовании задействованы студенты 1 курса направления «Архитектура» и группа старшеклассников, решивших посвятить себя архитектуре.
Методы исследования – анализ процесса выполнения графических работ по начертательной геометрии и черчению.
Обратимся к физиологическим особенностям организма человека. Как известно, наш мозг состоит из двух полушарий: левого и правого. Каждое полушарие управляет противоположной стороной тела человека и выполняет лучше ту работу, за которую оно отвечает. Исследования нейропсихологов и психоаналитиков [3] в области «межполушарной специализации мозга» свидетельствуют о том, что левое полушарие контролирует речь, отвечает за логику и анализ, поэтапно обрабатывает информацию. Правое полушарие воспринимает информацию, выраженную в символах и образах; способно рассматривать и обрабатывать сразу много информации, не применяя анализа; даёт возможность применения творческих способностей.
Таким образом, за логическое мышление отвечает левое полушарие, за творческое – правое полушарие головного мозга. Людей, обладающих равномерно развитыми полушариями головного мозга, очень мало [4]. У большинства из них доминирующим является одно из полушарий. Оно и определяет способности и возможности человека.
Теперь попробуем разобраться в приведённых ранее наблюдениях.
Объяснение материала преподаватель, как правило, сопровождает пространственными рисунками. Поэтому каждый шаг построения на ортогональном чертеже студенту понятен. Задание на самостоятельную работу дано в ортогональных проекциях. Студентам с правополушарным мышлением сложно представить в целом конечный результат. Отсюда и возникают трудности в выполнении задания. По той же причине таким студентам легче решать задачи с объёмным изображением (перспективой или аксонометрией), чем с абстрактным (пересечение прямой линии с плоскостью).
В олимпиаде принимают участие обычно сильные студенты. Но успеха добиваются только левополушарные студенты. Для решения олимпиадных задач требуется логическое мышление с умением анализировать ситуацию. Для творческого конкурса нужна фантазия. Здесь успех сопутствует правополушарным студентам.
Выполняя задание по проекционному черчению, одни школьники разбивают деталь на простейшие геометрические тела и без труда строят третью проекцию. У них работает логическое мышление. Значит, доминирующим является левое полушарие. Школьники с доминирующим правым полушарием затрудняются в построении третьей проекции. Поэтому они сначала строят наглядное изображение детали в аксонометрии, затем, глядя на неё, выполняют ортогональную проекцию.
Теперь становится понятным, почему студенты, блестяще справившиеся с заданием, затрудняются дать теоретические обоснования своим построениям. Ведь речь контролирует левое полушарие. А у этих студентов доминирует правое полушарие.
Как организовать учебный процесс так, чтобы обеспечить формирование нужных компетенций у всех студентов? Вопросам обучения детей с учётом развитости их полушарий посвящены труды нейропсихолога, доктора психологических наук, профессора А.Л. Сиротюк. Ею разработано практическое руководство для учителей и родителей [5]. Кандидат педагогических наук, доцент Н.В. Кайгородцева в своих исследованиях выясняет, что причины трудностей, возникающих при изучении «геометрических понятий и явлений», также связаны с работой полушарий головного мозга [4]. Студенты с первого семестра изучают начертательную геометрию. Обеспечить индивидуальное обучение на этом этапе практически невозможно, но организовать процесс обучения так, чтобы он способствовал дальнейшему развитию функций головного мозга, в компетенции преподавателя.
Поделимся собственным опытом. Изучение теоретического материала по начертательной геометрии обязательно сопровождается выполнением практических заданий. На закрепление одной и той же темы студентам можно предложить разноплановые задачи, предварительно объяснив, в чём их различие и какая цель при этом преследуется.
Так, изучив первый раздел «Конструирование геометрических моделей», в качестве эксперимента студентам предложили два вида заданий: «Конструирование плоской фигуры» и «Конструирование архитектурной оболочки». В первом задании требовалось построить проекции плоской фигуры по заданным условиям. Студентам необходимо было провести анализ условия задания, составить план решения задачи и используя выученный теоретический материал, выполнить построение. Это задание на чисто логическое мышление. Задача имеет вполне конкретное решение. Во втором задании дан план сооружения. Необходимо сконструировать из линейчатых поверхностей его покрытие, используя заданные формы направляющих. Эта задача носит творческий характер. Здесь может быть несколько вариантов. Всё зависит от фантазии студента. Подобные альтернативные задания, несомненно, будут способствовать совершенствованию одного и развитию другого мышления.
Эксперимент проводился в двух формах. Первый раз студентам предложили выполнить одно из двух заданий на выбор. В результате 16 % выбрали плоскую фигуру, остальные предпочтение отдали архитектурной оболочке. Во второй раз оба задания сделали обязательными, но ограничили время их выполнения. После установленного срока дорабатывать можно было одно из этих заданий. В результате 20 % выполнили оба задания, 3 % продолжили работу над плоской фигурой, остальные заканчивали архитектурную оболочку. Таким образом, мы выяснили, что большинство наших студентов обладают творческим мышлением. Поэтому необходимо обратить внимание на левое полушарие, отвечающее за логическое мышление.
Для развития логического мышления полезно решение конструктивных задач на только что изученную тему другого раздела. Так в разделе «Позиционные задачи» изучают методы определения взаимного расположения заданных геометрических объектов пространства. В конструктивных задачах сначала надо сконструировать геометрические объекты, а затем определять их взаимное расположение изученными методами.
К примеру, возьмём тему «Пересечение поверхностей. Метод сфер» [6, с. 69–76].
Могут использоваться концентрические и эксцентрические сферы.
Метод концентрических сфер применяется, когда:
- заданы две поверхности вращения,
- оси поверхностей пересекаются,
- плоскость осей параллельна одной из плоскостей проекций [6, с. 70].
Рассмотрим конструктивную задачу.
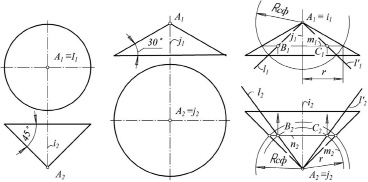
Задача 1. Через точку А провести прямые под углом 45 ° к π1 и 30 ° к π2.
Через точку можно провести много прямых линий под заданным углом к плоскости. Все они будут лежать на конической поверхности.
Геометрическим множеством всех прямых, проходящих через точку А под углом 45 ° к π1, является прямой круговой конус с вершиной в точке А, осью i ^ π1 и углом при основании 45 ° (рис. 1, а).
а) б) в)
Рис. 1. Задача 1: в ортогональных проекциях а) конус с осью i ^π1 , б) конус с осью j ^π2 , в) решение задачи
Геометрическим множеством всех прямых, проходящих через точку А под углом 30 ° к π2, является прямой круговой конус с вершиной в точке А, осью j ^ π2 и углом при основании 30 ° (рис. 1, б).
Прямые линии, удовлетворяющие всем условиям, должны принадлежать линии пересечения этих конусов.
Имеем две поверхности вращения, оси которых пересекаются: i ∩ j = А и лежат в плоскости, параллельной π3. Есть все условия для применения концентрических сфер. Поскольку конусы имеют общую вершину (точку А), то они пересекаются по образующим. Поэтому достаточно воспользоваться только одной вспомогательной сферой, что и показано на рис. 1, в.
Поскольку основания конусов в решении задачи не используются, то каждый конус на эпюре задан только одной проекцией. Вспомогательная сфера проведена из центра А в двух проекциях.
Если при решении задачи методом концентрических сфер окажется, что сфера минимального радиуса касается одновременно каждой заданной поверхности, то применяется теорема Монжа [6, с. 74].
Если две поверхности вращения описаны около третьей поверхности вращения или вписаны в неё, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через точки касания.
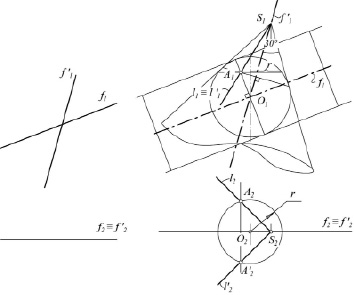
Задача 2. Даны две пересекающиеся фронтали f и f'. Провести прямые, удалённые от фронтали f на расстоянии 40 мм и пересекающие фронталь f' под углом 30 ° (рис. 2, а).
Прямые линии, удалённые от фронтали f на 40 мм, должны быть либо образующими прямого кругового цилиндра с осью f, либо прямыми, касающимися этого цилиндра.
Прямые линии, пересекающие фронталь f' под углом 30 °, должны быть образующими прямого кругового конуса с осью f' и углом при вершине 30 °.
Таким образом, мы имеем две поверхности вращения, их оси пересекаются и лежат в плоскости, параллельной π1. Значит, для решения можно использовать концентрические сферы, проводимые в плоскости π1. О1 – центр сфер.
Искомые прямые линии должны быть образующими конуса, касающимися цилиндра. Это возможно в том случае, когда конус и цилиндр описаны около одной сферы. Поскольку диаметр цилиндра 40 мм, то и диаметр вписанной в него сферы тоже 40 мм. В данном случае имеет место теорема Монжа и для решения задачи понадобится только одна сфера.
Построение в ортогональных проекциях приведено на рис. 2, б.
В плоскости π1 из О1 проводим очерк сферы диаметром 40 мм. Параллельно f1 проводим очерковые образующие цилиндра. Под углом 30 ° к f' проводим очерковые образующие конуса так, чтобы они касались очерка сферы. При пересечении их с f1' отмечаем вершину конуса S1. По линии связи переносим её на f2'.
Соединив точки касания очерка сферы с очерковыми образующими цилиндра и конуса, получим проекции линий касания сферы с каждой из этих поверхностей. Точка А1 их пересечения будет фронтальной проекцией точки касания образующих цилиндра и конуса. Её горизонтальные проекции найдём через сферу. Прямые l (l1, l2) и l'(l1', l2' ) будут искомыми.
а) б)
Рис. 2. Задача 2: а) условие, б) решение в ортогональных проекциях
Метод эксцентрических сфер применяется, когда:
- заданы две криволинейные поверхности, из которых хотя бы одна является поверхностью вращения, а другая может пересекаться плоскостями по семейству окружностей;
- обе поверхности имеют общую плоскость симметрии;
- плоскость симметрии параллельна одной из плоскостей проекций [6, с. 74].
Задача 3. Задан конус вращения, осью которого является фронталь f, и горизонтально расположенная окружность. Центр О окружности находится в одной плоскости с фронталью f. Определить точки пересечения окружности с поверхностью конуса, не прибегая к построению лекальных кривых (рис. 3, а).
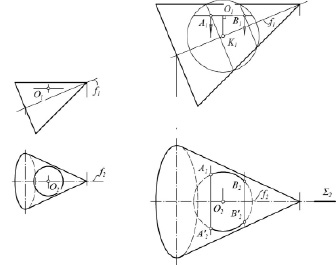
а) б)
Рис. 3. Задача 3: а) условие, б) решение в ортогональных проекциях
Заданы две фигуры: поверхность вращения (конус) и горизонтально расположенная окружность. Поскольку центр О окружности находится в одной плоскости с осью f конуса, то обе фигуры имеют общую плоскость симметрии Σ. А так как f – фронталь, то Σ ?π1. Таким образом, имеются все условия для применения метода эксцентрических сфер. Здесь вместо второй поверхности задана одна окружность. Задачу можем решить при помощи сферы (рис. 3, б). Её центр K1 находится в точке пересечения срединного перпендикуляра, проведённого из центра проекции окружности, с осью конуса. Проведённая сфера соосна с конусом. Она пересекает его по окружностям, проекции которых проходят через точки пересечения очерков. На пересечении построенных линий с заданной окружностью получаются проекции А1 и В1 искомых точек.
Каждая из рассмотренных выше конструктивных задач была «привязана» к конкретной позиционной задаче на пересечение поверхностей. Это облегчало проведение анализа и создание логических цепочек для конструирования геометрического объекта, поскольку было ясно, модель какой ситуации необходимо создать. Такое «сопровождение» можно организовать для всех позиционных и метрических задач. Оно оказывает неоценимую помощь в развитии левого полушария, отвечающего за логику.
В заключение хочется отметить, что обучение – это обоюдотворческий процесс. Его следует организовать так, чтобы было интересно и педагогу, и обучаемому. Нельзя преподавать по шаблону. Творчески мыслящий педагог может сам составить подобное «сопровождение» ко всем темам, а также продумать другие приёмы развития личности в процессе обучения.



