Ввод государственного стандарта образования в вузах двухуровневого образования бакалаврита и магистратуры, а также третий уровень – профессиональное образование включает не только развитие навыков самоопределения будущего бакалавра, но и комплексный подход к получению образования, формированию умений, принятию важных решений, обучению самостоятельной работе и ответственности за принятые решения.
Во многих случаях развитие профессиональных навыков студентов зависит от индивидуальных качеств, самостоятельное развитие уровня обучения формирует исследовательскую компетентность.
В процессе обучения цель преподавателя – быть организатором, а студент становится предметом объекта исследования.
Использование условных возможностей в сфере образования помогает студенту бакалавру достичь поставленных целей с формированием целенаправленных исследовательских компетенций [1], выполненных отмеченных умений. Вместе с тем освоение учебных материалов на занятиях в вузах во многих случаях используются традиционные формы, методы и средства обучения.
Отмечая точнее, средства информационных коммуникационных сфер, как отмечено все вышесказанное приводят к необходимости формирования исследовательских компетенций будущих специалистов [2].
Организация исследовательской работы математиков в условиях дистанционного обучения:
– проблема формирования исследовательской компетенции с применением информационных технологий на практике полностью не решена, так, например, в процессе дистанционного обучения не реализована активная связь между студентом и преподавателем, а также между студентами;
– уровень образования студентов дистанционной формы обучения оценивается в виде тестов, что ограничивает их возможности, что препятствует формированию исследовательских компетенций;
– не формируется соответствующая деятельность профессиональной методической подготовки будущих математиков бакалавров.
На сегодняшний день в вузах встает вопрос, в чем проблема недобора бюджетных мест на специальности математика. Но нас огорчает то, что наш учебный план не полностью реализован. Так как при дистанцианной форме обучения мы полностью обучаем по учебному плану. На сегоднящний момент нам не известно, на каком уровне компетентен математик бакалавр, обучающийся на дистанционной форме. На данный момент мы подготовили первых математиков студентов, окончивших дистанционную форму обучения, и нам теперь неизвестно, какими они будут педагогами, как они будут готовить будущее поколение. До этого мы слышали мнение, что уровень студентов заочников неудовлетворительный, что недостаток их знаний нанес урок ученикам, сейчас мы, используя дистанционную технологию обучения, применяем заочную форму обучения.
В основном подготовка математиков не на дистанционном, а на дневном обучении трудна, а знания студентов, обучающихся дистанционно, ограничиваются тестом.
Поэтому предлагаемая нами технология применения портфолио на заочной форме обучения с использованием дистанционной технологии обучения показала свою эффективность в проведенных наших экспериментах. Здесь студент, применяя технологию портфолио, в конце каждого семестра защищает все собранное электронное портфолио перед студентами, обсуждаются появившиеся вопросы и итоги оцениваются вместе, реализуются активные элементы и формируется взаимооценивание [3]. Это, с одной стороны дает толчок к полной реализации учебного плана, с другой стороны, формирует необходимые профессиональные компетенции будущего педагога.
Основная цель создания портфолио и ожидаемые итоги – это создание каждым студентом согласно успеваемости математического портфолио, добавление текущих качественных компонентов курсовых портфолио, представление итогов текущих занятий семетра.
Индивидуальное электронное образовательное портфолио студента, соответствующее высшему профессиональному учебному стандарту, полностью представляет итоги знаний студентов.
На представленном ниже рисунке показано формирование модели исследовательской компетенции математика бакалавра с использованием технологии портфолио, где со стороны студентов ведение портфолио помогает реализовать основную функцию педогогического контроля (аттестации).
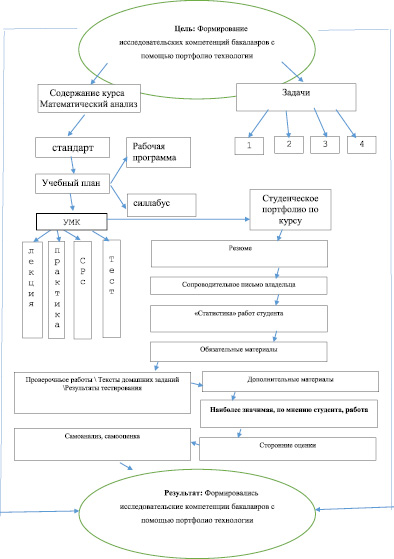
Модель дистанционного образования с применением технологии портфолио
Здесь, с одной стороны, связь студента и преподавателя, с другой стороны, форма организации учебного процесса в одно и то же время контролирует качество и модели обучения.
Эту модель мы применили при подготовке математиков бакалавров при обучении дисциплины «Математический анализ», входящего в учебный план по основной образовательной программе 550200 Математика к характеристике профессиональной деятельности (ПД) выпускников, освоивших программу бакалавриата, в соответствии с видами ПД, на которые ориентирована программа бакалавриата, должен быть готов решать профессиональные задачи в соответствии с ГОС ВПО Кыргызской Республики.
Если, к примеру, взять дисциплину «Математический анализ» за 2–3 курсы (4, 5, 6 семестры), то годовое содержание этой учебной дисциплины можно разделить на 6 учебных модулей. С учетом значительного места дисциплины «Математический анализ» в профессиональном блоке оправдана «загруженность» структурной матрицы формирования профессиональной подготовки по каждому из 6 учебных модулей. Ключевыми звеньями ПМК бакалавров по основной образовательной программе 550200 Математика на 2, 3 курсах являются учебные модули «Дифференциальное исчисление функции одной переменной» и «Интегральное исчисление функции одной переменной». Знания и опыт, полученные студентом при изучении данных разделов, в основном определяют последующее совершенствование профессиональной математической деятельности студентов [4]. Нелегко подобрать и задания, которые объективно диагностируют ту или иную профессиональную компетенцию.
Экспериментальная работа включала три этапа: констатирующий (2012–2013 гг.), формирующий (2013–2015 гг.) и контрольный (2015–2017 гг.).
Первый этап (2012–2013 гг.) был посвящен изучению и анализу педагогической, научно-методической литературы по теме исследования. Определены: цель, задачи, объект, предмет, этапы исследования; предложено использование портфолио по программе AVN; осуществлен отбор экспериментальных материалов; проводилась поисковая работа.
На втором этапе (2013–2015 гг.) был определен состав исследовательских компетенций будущих бакалавров при изучении матеметических дисциплин в вузах педагогического направления; были даны определения понятиям «исследовательская компетенция», исследовательские компетенции; «исследовательская компетентность», было определено инвариантное ядро понятия «исследовательская компетенция». была проведена опытно-экспериментальная работа, в целях проверки эффективности использования портфолио по программе AVN в условиях дистантной формы обучения в вузах.
Третий этап (2015–2017 гг.). Была осуществлена опытно-экспериментальная работа, в ходе которой реализовывалась предложенная методика использования портфолио по программе AVN в условиях дистантной формы обучения, проверялась ее эффективность.
При организации педагогического эксперимента были поставлены следующие цели:
1. Разработать методические рекомендации использования портфолио на основе программы AVN в условиях дистантного обучения в вузах.
2. Проверить эффективность развития ИК студентов дистантного обучения в результате использования портфолио.
Для достижения этих целей был разработан следующий план действий:
– определение контрольных и экспериментальных групп;
– создание портфолио для каждой группы студентов;
– проведение теста для констатации уровня усвоения учебного материала для каждой группы;
– анализ полученных результатов и выработка соответствующих положений.
Согласно поставленным задачам вначале был проведен констатирующий эксперимент. В эксперименте участвовали студенты из факультета физико-математического образования и информационных технологии (ФМОиИТ), 73 студента, а также из института повышения квалификации и переподготовки кадров (ИПКиПК) 86 студентов КГУ им. И. Арабаева и из ИГУ им. К.Тыныстанова 48 студентов. В контрольных группах занятия по дисциплине «Математический анализ» проводились по традиционной методике (с применением обычных учебников и учебных пособий), а в экспериментальных группах использовались возможности ИКС с целью сравнения эффективности традиционной методики и технологии портфолио в условиях дистантного обучения.
На первом этапе экспериментального исследования получен первичный эмпирический материал, который позволил определить исходный уровень усвоения студентами материалов дисциплины «Математический анализ», и на основе этого была предложена технология портфолио в виртуальной образовательной среде. Для развития ИК математиков бакалавров разработаны модель и методические рекомендации его реализации.
На втором этапе экспериментального исследования была разработана технология портфолио для развития ИК математиков бакалавров, применялось в дисциплине «Математический анализ».
На третьем этапе экспериментального исследования были получены результаты взаимодействия студентов и преподавателя, студентов со студентами в процессе обучения, подведены итоги работы с портфолио в виртуальной среде AVN и определены уровни сформированности ИК бакалавров математиков.
На основании результатов проведенных экспериментов составлена табл. 1.
Таблица 1
Значения оценок и вероятностей, 2013–2014 у.г.
|
xi |
x1 < 55 |
55 ≤ x2 < 70 |
70 ≤ x3 < 85 |
x4 ≥ 85 |
|
pi (контр.) |
0,055 |
0,362 |
0,472 |
0,109 |
|
pi (эксп.) |
0,044 |
0,233 |
0,557 |
0,166 |
Таблица 2
Значения оценок и вероятностей, 2014–2015 у.г.
|
xi |
x1 < 55 |
55 ≤ x2 < 70 |
70 ≤ x3 < 85 |
x4 ≥ 85 |
|
pi (контр.) |
0,065 |
0,376 |
0,441 |
0,118 |
|
pi (эксп.) |
0,011 |
0,247 |
0,539 |
0,203 |
Таблица 3
Значения оценок и вероятностей, 2015–2016 у.г.
|
xi |
x1 < 55 |
55 ≤ x2 < 70 |
70 ≤ x3 < 85 |
x4 ≥ 85 |
|
pi (контр.) |
0,043 |
0,336 |
0,490 |
0,131 |
|
pi (эксп.) |
0,011 |
0,114 |
0,602 |
0,273 |
Далее проанализируем дисциплину «Математический анализ» за каждый год после внедрения технологии портфолио на дистанционную форму обучения.
За 2013–2014 учебный год численные значения математического ожидания по вышеприведенной формуле – произведены следующие вычисления.
Контрольная диагностика:
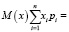 x1*p1 + x2*p2 + x3*p3 + x4*p4 =
x1*p1 + x2*p2 + x3*p3 + x4*p4 =
= 5*0,055 + 33*0,362 + 43*0,472 + 10*0,109 =
= 0,275 + 11,946 + 20,296 + 1,09 = 33,607.
Экспериментальная диагностика:
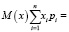 x1*p1 + x2*p2 + x3*p3 + x4*p4 =
x1*p1 + x2*p2 + x3*p3 + x4*p4 =
= 3*0,044 + 21*0,233 + 51*0,557 + 15*0,166 =
= 0,132 + 4,893 + 28,407 + 2,49 = 35,922.
За 2014–2015 учебный год численные значения математического ожидания по вышеприведенной формуле произведены следующие вычисления.
Контрольная диагностика:
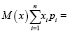 x1*p1 + x2*p2 + x3*p3 + x4*p4 =
x1*p1 + x2*p2 + x3*p3 + x4*p4 =
= 6*0,065 + 35*0,376 + 41*0,441 + 11*0,118 =
= 0,39 + 13,16 + 18,081 + 1,298 = 32,929.
Экспериментальная диагностика:
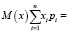 x1*p1 + x2*p2 + x3*p3 + x4*p4 =
x1*p1 + x2*p2 + x3*p3 + x4*p4 =
= 1*0,011 + 22*0,247 + 48*0,539 + 18*0,203 =
= 0,011 + 5,434 + 25,872 + 3,654 = 34,971.
За 2015–2017 учебный год численные значения математического ожидания по вышеприведенной формуле произведены следующие вычисления.
Контрольная диагностика:
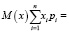 x1*p1 + x2*p2 + x3*p3 + x4*p4 =
x1*p1 + x2*p2 + x3*p3 + x4*p4 =
= 4*0,043 + 31*0,336 + 45*0,490 + 12*0,131 =
= 0,172 + 10,416 + 22,05 + 1,572 = 34,21.
Экспериментальная диагностика:
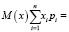 x1*p1 + x2*p2 + x3*p3 + x4*p4 =
x1*p1 + x2*p2 + x3*p3 + x4*p4 =
= 1*0,011 + 10*0,114 + 53*0,602 + 24*0,273 =
= 0,011 + 1,14 + 31,906 + 6,552 = 39,609.
Значения математического ожидания за 2013–2017 учебные годы показаны в табл. 4.
Таблица 4
Показатели математического ожидания по учебным годам
|
Учебные годы |
Контр. груп. М(х) |
Экспер. груп. М(х) |
|
2013–2014 у.г. |
33,607 |
35,922 |
|
2014–2015 у.г. |
32,929 |
34,971 |
|
2015–2017 у.г. |
34,21 |
39,609 |
После изучения дисциплины «Математический анализ» исследовательские компетенции бакалавра математика если не полностью, то можно считать, что повысились. Развитие исследовательских компетенций математика бакалавра с использованием информационных технологий приводит к увеличению интереса к предмету. При обучении курса предложенная нами технология портфолио с каждым годом развивалась, вносились дополнения и доказана проведенными экспериментами эффективность учебного плана [5].



