Современные мировые и российские условия требуют от выпускников вузов наличия высокой квалификации, готовности к продуктивной творческой профессиональной деятельности, способности комплексно сочетать исследовательскую, проектную и предпринимательскую деятельность для поддержания их конкурентоспособности [1]. Эффективным механизмом формирования данных качеств в системе высшего образования является сетевое взаимодействие [2], позволяющее совместно использовать материальные и педагогические ресурсы нескольких вузов.
Так как в российской высшей школе большой накопленный опыт подобного взаимодействия отсутствует, существует ряд проблем, с которыми сталкиваются вузы при организации сетевой формы взаимодействия и управлении этим взаимодействием. Поэтому в последнее время большое внимание уделяется вопросам проектирования и условиям реализации сетевых программ, анализу роли вуза в академической сети и оценке качества его работы, а также принципам организации сетевого взаимодействия [4].
Вопросы управления индивидуальными учебными планами студентов (ИУП) занимают важное место в организации сетевой формы взаимодействия вузов, однако они до сих пор не решены [7]. Задача нахождения оптимальных ИУП студентов относится к классу np-сложных задач дискретной оптимизации, и огромное количество допустимых решений на реальных примерах не позволяет применять метод полного перебора. Для её решения был успешно применен эвристический метод, в основе которого находятся генетические алгоритмы и который подробно описан в [6].
В данной статье этот алгоритм будет рассмотрен на примере решения задачи построения ИУП студентов, обучающихся в международной магистратуре «Обеспечение технологических процессов жизненного цикла изделия», в рамках международного проекта «Успех» («Success») (544019-TEMPUS-1-2013-1-ATTEMPUS-JPCR), проектирование согласованного учебного плана которой приведено в [3].
Постановка задачи
Условия данной задачи можно сформулировать следующим образом. Пусть сетевую магистерскую программу реализуют 4 вуза: ВУЗ1, ВУЗ2, ВУЗ3, ВУЗ4. Сама сетевая программа состоит из 4 модулей, каждый из которых имеет трудоемкость 30 зачетных единиц и реализуется в течение одного семестра. По договоренности между вузами в рамках данной сетевой программы студенты могут пройти только один – третий по счету модуль в любом вузе-партнере, остальные модули должны были быть изучены в базовом вузе.
Считается, что каждый вуз набрал по 10 студентов. Таким образом, общее количество студентов, обучающихся на сетевой программе – 40 человек, каждый из которых должен изучить 1 модуль в другом вузе (третий по счету). Каждый вуз установил ограничения на количество студентов, которые в нем могут изучать согласованный учебный модуль: от 8 до 12. Каждый студент определил свои предпочтения по изучению модуля в каждом из вузов. Данные предпочтения представлены в табл. 1 (где 1 соответствует наибольшему желанию студента изучить модуль в вузе, а 0 – наименьшему).
Так как прохождение одного модуля в другом вузе является обязательным условием рассматриваемой программы, желания изучения модуля в собственном, базовом вузе не собирались и в соответствующих ячейках в табл. 1 проставлены «–».
Требуется найти такое распределение студентов по вузам для изучения третьего модуля, при котором бы медиана их удовлетворенности (соответствующий коэффициент из табл. 1) была максимальна, и ограничения для каждого вуза на количество студентов, изучающих этот модуль в его стенах, были бы удовлетворены. При этом считается, что в индивидуальном учебном плане каждого студента первый, второй и четвертый модули сетевой образовательной программы должны быть изучены в базовом для студента вузе (в который он поступил), а третий должен быть изучен в другом вузе-партнере.
Данная задача является частным случаем общей задачи построения ИУП студентов, обучающихся на сетевой образовательной программе, которая подробно описана в [5].
Таблица 1
Предпочтения студентов
|
Студент |
Базовый вуз |
ВУЗ1 |
ВУЗ2 |
ВУЗ3 |
ВУЗ4 |
|
1 |
ВУЗ1 |
– |
0,6 |
0,1 |
0,1 |
|
2 |
ВУЗ1 |
– |
0,8 |
0,6 |
0,3 |
|
3 |
ВУЗ1 |
– |
0,5 |
0,6 |
0,6 |
|
4 |
ВУЗ1 |
– |
0,4 |
0,3 |
0,5 |
|
5 |
ВУЗ1 |
– |
0,1 |
0,2 |
0,7 |
|
6 |
ВУЗ1 |
– |
0,3 |
0,5 |
0,4 |
|
7 |
ВУЗ1 |
– |
0,6 |
0,2 |
0,3 |
|
8 |
ВУЗ1 |
– |
0,2 |
0,4 |
0,6 |
|
9 |
ВУЗ1 |
– |
0,6 |
0,6 |
0,5 |
|
10 |
ВУЗ1 |
– |
0,5 |
0,7 |
0,4 |
|
11 |
ВУЗ2 |
1 |
– |
0,6 |
0,1 |
|
12 |
ВУЗ2 |
1 |
– |
0,8 |
0,6 |
|
13 |
ВУЗ2 |
1 |
– |
0,5 |
0,6 |
|
14 |
ВУЗ2 |
1 |
– |
0,4 |
0,3 |
|
15 |
ВУЗ2 |
1 |
– |
0,1 |
0,2 |
|
16 |
ВУЗ2 |
1 |
– |
0,3 |
0,5 |
|
17 |
ВУЗ2 |
1 |
– |
0,6 |
0,2 |
|
18 |
ВУЗ2 |
1 |
– |
0,2 |
0,4 |
|
19 |
ВУЗ2 |
1 |
– |
0,6 |
0,6 |
|
20 |
ВУЗ2 |
1 |
– |
0,5 |
0,7 |
|
21 |
ВУЗ3 |
1 |
0,6 |
– |
0,1 |
|
22 |
ВУЗ3 |
1 |
0,8 |
– |
0,6 |
|
23 |
ВУЗ3 |
1 |
0,5 |
– |
0,6 |
|
24 |
ВУЗ3 |
1 |
0,4 |
– |
0,3 |
|
25 |
ВУЗ3 |
1 |
0,1 |
– |
0,2 |
|
26 |
ВУЗ3 |
1 |
0,3 |
– |
0,5 |
|
27 |
ВУЗ3 |
1 |
0,6 |
– |
0,2 |
|
28 |
ВУЗ3 |
1 |
0,2 |
– |
0,4 |
|
29 |
ВУЗ3 |
1 |
0,6 |
– |
0,6 |
|
30 |
ВУЗ3 |
1 |
0,5 |
– |
0,7 |
|
31 |
ВУЗ4 |
1 |
0,6 |
0,1 |
– |
|
32 |
ВУЗ4 |
1 |
0,8 |
0,6 |
– |
|
33 |
ВУЗ4 |
1 |
0,5 |
0,6 |
– |
|
34 |
ВУЗ4 |
1 |
0,4 |
0,3 |
– |
|
35 |
ВУЗ4 |
1 |
0,1 |
0,2 |
– |
|
36 |
ВУЗ4 |
1 |
0,3 |
0,5 |
– |
|
37 |
ВУЗ4 |
1 |
0,6 |
0,2 |
– |
|
38 |
ВУЗ4 |
1 |
0,2 |
0,4 |
– |
|
39 |
ВУЗ4 |
1 |
0,6 |
0,6 |
– |
|
40 |
ВУЗ4 |
1 |
0,5 |
0,7 |
– |
Решение задачи
Таким образом, целевая функция задачи принимает следующий вид W = Me(w1, …, wS), где wi – коэффициент удовлетворенности i-го студента текущим решением.
Под точностью решения будем понимать отношение значения целевой функции найденного решения к максимальному значению целевой функции для данной задачи, умноженное на 100 %. Для оценки точности решения, полученного при помощи генетического алгоритма, было найдено максимальное значение целевой функции описанной задачи методом полного перебора, которое оказалось равно 0,7.
Так как точность генетических алгоритмов имеет вероятностный характер, то будет выполняться ряд запусков алгоритма, на основании которых будут делаться выводы о точности решения в статистическом смысле. Будем считать приемлемой точностью для данной задачи точность не ниже 80 % в 80 % запусков [6].
Результат, полученный после серии запусков алгоритма, представлен в табл. 2.
В полученном решении значение целевой функции равно 0,7. Точность решения при этом равна 100 %. График, отражающий вероятность достижения заданной точности для рассматриваемой задачи, представлен на рисунке.
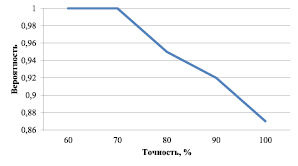
Вероятность достижения точности
В представленном решении распределение студентов по вузам, в которых они изучают третий модуль, выглядит следующим образом:
1. ВУЗ1 – 12
2. ВУЗ2 – 10
3. ВУЗ3 – 9
4. ВУЗ4 – 9
Данное распределение удовлетворяет обозначенным ограничениям вузов. Из результатов, представленных в табл. 2, видно, что для 22 студентов был выбран наиболее приоритетный, с их точки зрения, вуз, для остальных – второй по приоритетности. То есть нет ни одного студента, для которого бы был выбран наименее приоритетный вуз.
Таблица 2
Распределение студентов на третий модуль
|
Студент |
Базовый вуз |
Выбранный вуз, коэффициент удовлетворенности студента и уровень выбранного приоритета |
Студент |
Базовый вуз |
Выбранный вуз, коэффициент удовлетворенности студента и уровень выбранного приоритета |
|
1 |
ВУЗ1 |
ВУЗ2 (0,6) – 1 |
21 |
ВУЗ3 |
ВУЗ2 (0,6) – 2 |
|
2 |
ВУЗ1 |
ВУЗ2 (0,8) – 1 |
22 |
ВУЗ3 |
ВУЗ2 (0,8) – 2 |
|
3 |
ВУЗ1 |
ВУЗ4 (0,6) – 1 |
23 |
ВУЗ3 |
ВУЗ4 (0,6) – 2 |
|
4 |
ВУЗ1 |
ВУЗ4 (0,5) – 1 |
24 |
ВУЗ3 |
ВУЗ1 (1) – 1 |
|
5 |
ВУЗ1 |
ВУЗ4 (0,7) – 1 |
25 |
ВУЗ3 |
ВУЗ1 (1) – 1 |
|
6 |
ВУЗ1 |
ВУЗ3 (0,5) – 1 |
26 |
ВУЗ3 |
ВУЗ1 (1) – 1 |
|
7 |
ВУЗ1 |
ВУЗ2 (0,6) – 1 |
27 |
ВУЗ3 |
ВУЗ2 (0,6) – 2 |
|
8 |
ВУЗ1 |
ВУЗ4 (0,6) – 1 |
28 |
ВУЗ3 |
ВУЗ1 (1) – 1 |
|
9 |
ВУЗ1 |
ВУЗ2 (0,6) – 1 |
29 |
ВУЗ3 |
ВУЗ4 (0,6) – 2 |
|
10 |
ВУЗ1 |
ВУЗ3 (0,7) – 1 |
30 |
ВУЗ3 |
ВУЗ4 (0,7) – 2 |
|
11 |
ВУЗ2 |
ВУЗ3 (0,6) – 2 |
31 |
ВУЗ4 |
ВУЗ2 (0,6) – 2 |
|
12 |
ВУЗ2 |
ВУЗ3 (0,8) – 2 |
32 |
ВУЗ4 |
ВУЗ2 (0,8) – 2 |
|
13 |
ВУЗ2 |
ВУЗ4 (0,6) – 2 |
33 |
ВУЗ4 |
ВУЗ3 (0,6) – 2 |
|
14 |
ВУЗ2 |
ВУЗ1 (1) – 1 |
34 |
ВУЗ4 |
ВУЗ1 (1) – 1 |
|
15 |
ВУЗ2 |
ВУЗ1 (1) – 1 |
35 |
ВУЗ4 |
ВУЗ1 (1) – 1 |
|
16 |
ВУЗ2 |
ВУЗ1 (1) – 1 |
36 |
ВУЗ4 |
ВУЗ1 (1) – 1 |
|
17 |
ВУЗ2 |
ВУЗ3 (0,6) – 2 |
37 |
ВУЗ4 |
ВУЗ2 (0,6) – 2 |
|
18 |
ВУЗ2 |
ВУЗ1 (1) – 1 |
38 |
ВУЗ4 |
ВУЗ1 (1) – 1 |
|
19 |
ВУЗ2 |
ВУЗ3 (0,6) – 2 |
39 |
ВУЗ4 |
ВУЗ3 (0,6) – 2 |
|
20 |
ВУЗ2 |
ВУЗ4 (0,7) – 2 |
40 |
ВУЗ4 |
ВУЗ3 (0,7) – 2 |
При этом представленное распределение студентов не является единственно возможным с максимальным значением целевой функции в данных условиях. К примеру, может быть изменено распределение студентов под номерами 26 и 39 (альтернативное распределение представлено в табл. 3).
Таблица 3
Альтернативное распределение студентов на третий модуль
|
Студент |
Базовый вуз |
Выбранный вуз, предпочтение студента и номер выбранного приоритета |
|
26 |
ВУЗ3 |
ВУЗ4 (0,5) – 2 |
|
39 |
ВУЗ4 |
ВУЗ1 (1) – 1 |
На этом примере можно видеть возможность выбора из множества оптимальных решений, полученных с помощью генетического алгоритма, необходимого распределения студентов лицом, принимающим решения (ЛПР). При этом ЛПР при выборе «наилучшего» решения может учитывать дополнительные приоритеты студентов, например их успехи в обучении в базовом вузе, материальные возможности студентов и т.п. Такой подход делает полученное решение более «справедливым» и максимально учитывает предпочтения студентов.
Заключение
Было рассмотрено применение описанного в [6] метода построения индивидуальных учебных планов студентов в условиях сетевого взаимодействия вузов, в основе которого лежит генетический алгоритм. Результаты его применения являются приемлемыми (точность 100 % достигается в 87 % случаев, точность 90 % достигается в 92 % случаев, точность 80 % достигается в 95 % случаев). Это позволяет сделать вывод о пригодности метода для решения задач составления индивидуальных учебных планов студентов, обучающихся на сетевой образовательной программе, с учетом их предпочтений.



