Одним из основных свойств, обеспечивающих качество объектов машиностроения, является геометрическая точность корпусных деталей, таких как блоки цилиндров, корпуса редукторов, опоры валов и другие. Это базовые, системообразующие детали, которые обеспечивают рабочее положение других деталей, а значит, надежность и долговечность работы всего объекта.
Функциональными параметрами указанных деталей являются соосность, перпендикулярность, параллельность и пересечение осей отверстий. Для контроля этих параметров у крупногабаритных деталей (более 8 м) обычно используют визирный метод, который реализуется с помощью координатного оптического измерителя и указателя положения центра отверстия детали – центроискателя. Если применяемые измерители, как правило, являются универсальными устройствами (визирные измерительные трубы, цифровые автоколлиматоры), то центроискатели являются оригинальными устройствами. К настоящему времени существует в натуре и инженерных разработках множество моделей. Но, несмотря на все их разнообразие, задача создания универсального центроискателя не решена. Требуются конструктивные решения, обладающие новыми функциональными свойствами, принципом действия, используемыми материалами, различными габаритами, которые будут обеспечивать заданную точность фиксирования центра отверстия, а значит, и точность контроля базовых деталей [4].
Поэтому, проектируя новые модели или анализируя известные конструкции центроискателей, необходимо оценивать погрешность определения центра отверстия.
В настоящей работе показана возможность математического моделирования с использованием методов размерных цепей, Монте-Карло и вычислительной математики для оценки точности центроискателей. На основе указанных методов cоставлен алгоритм и проведено численное моделирование типового центроискателя при прямой (определении квалитета составляющих звеньев) и обратной (определении номинального размера и квалитета замыкающего звена) задачах.
Материалы и методы исследования
Объект исследования. Для разработки математической модели и проведения расчетов выбрана типовая схема центроискателя, показанная на рис. 1. Она состоит из целевого знака 1 (сетка с перекрестием или координатный фотоприемник), поворотного диска 2, разделенного на три сектора с переменным профилем, и трех опор 3. При развороте диска опоры смещаются до соприкосновения со стенкой отверстия. В результате целевой знак фиксируется в центре отверстия [10].
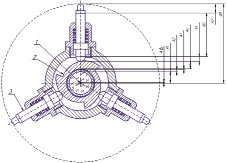
Рис. 1. Схема типового центроискателя и размерная цепь его опоры
Методика исследования. Действительное положение целевого знака в отверстии обеспечивается точностью деталей центроискателя и их сопряжением. Поэтому при оценке точности необходимо учитывать взаимосвязанные размеры, их квалитеты, отклонения, взаимовлияние друг на друга. Перечисленные задачи решаются с использованием теории размерных цепей (РЦ).
РЦ центроискателя составлена для одной опоры (рис. 1). Для остальных опор, из-за симметричности конструкции, РЦ аналогичны. Она представляет собой набор звеньев, где Аi – квалитеты сопрягаемых деталей, AΔ – отклонение целевого знака от центра отверстия.
Составленная РЦ опоры центроискателя позволяет решить две задачи. Рассчитать допуски и установить квалитеты составляющих звеньев исходя из заданных точностных требований к замыкающему звену. Установить номинальное значение и квалитет замыкающего звена по установленным квалитетам составляющих звеньев [8].
Исходя из того, что номинальные размеры, входящие в РЦ, имеют значения разных порядков, расчеты выполнены способом одного квалитета.
Необходимый квалитет аср определяется по формуле
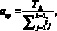(1)
где ТΔ – заданный допуск замыкающего звена, i – единица допуска, которая рассчитывается по формуле:
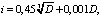(2)
где D – средний геометрический размер для интервала диаметров, к которому относится данный линейный размер [7].
При поверочном расчете (обратной задаче) параметры замыкающего звена определяются по следующим формулам.
Номинальный размер замыкающего звена:
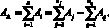(3)
Верхнее отклонение замыкающего звена:
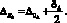(4)
Нижнее отклонение замыкающего звена:
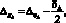(5)
где AΔ – номинальный размер замыкающего звена, Аi – номинальный размер любого составляющего звена, Аj – номинальный размер увеличивающего звена, Аq – номинальный размер уменьшающего звена, nj и nq – число увеличивающих и число уменьшающих звеньев, Δ????Δ и Δ????Δ – верхнее и нижнее отклонения замыкающего звена, Δ0Δ – координата середины поля допуска замыкающего звена, ????Δ – допуск на замыкающее звен
о.В реальной конструкции размеры составляющих звеньев являются случайными величинами. Следовательно, замыкающее звено РЦ также является случайной величиной. Поэтому возможно использовать в расчетах РЦ метод статистического моделирования (Монте-Карло), который наиболее приближен к реальной модели. Он основан на моделировании случайных значений номинальных размеров звеньев, распределенных в поле их допуска по заданному закону и с заданными вероятностными характеристиками. Перейдя от случайного сочетания погрешностей к случайному сочетанию размеров составляющих звеньев, находят i-ую реализацию результирующей погрешности [6
].При моделировании значений составляющих звеньев РЦ использовался наиболее универсальный закон рассеяния случайных величин – нормальный (Гаусса). Вместе с тем предлагаемая математическая модель позволяет использовать и другие функции распределения [2
].На основании изложенного разработан алгоритм и компьютерная программа расчета РЦ. На рис. 2 показана схема программы для расчета замыкающего звена РЦ с применением метода Монте-Карло [3
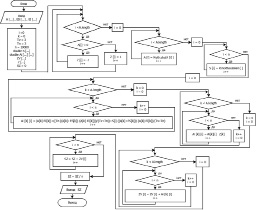
Рис. 2. Схема программы расчета замыкающего звена РЦ методом Монте-Карло
].Алгоритм построен следующим образом. Вначале производится ввод данных: A[…] – массив номинальных значений звеньев; ES[…] – верхнее отклонение звеньев; EI[…] – нижнее отклонение; Z[…] – массив для коэффициентов, определяющих тип звеньев; S[…] – массив значений, распределенных по закону Гаусса с математическим ожиданием, равным 0, и СКО, равным 1; ZV[…] – массив значений замыкающего звена; SZ – среднее значение замыкающего звен
а.Массив Ai[…][…] заполняется по формуле определения случайных значений звена в размерной цепи для нормального усеченного распределения. Переменные Tv и Tn – квантили распределения для односторонних доверительных вероятностей Yv и Yn, соответствующих верхней и нижней границам рассеяния размеров (для расчета Yv и Yn выбраны равными 0,99865, соответственно Tv и Tn = 3) [5
].Значение переменной, определяющей количество значений для каждого звена РЦ n, определяется необходимой точностью вычислений и может варьироваться в зависимости от вычислительной мощности компьютера
. На выходе получаем значение замыкающего звена – отклонение целевого знака центроискателя относительно центра контролируемого отверстия вдоль оси опор
ы.Реальное (рабочее) положение центроискателя предполагает его контакт со стенкой отверстия при помощи трех равномерно расположенных опор (рис. 3).
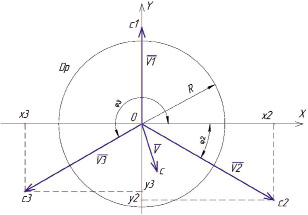
Рис. 3. Схема нахождения результирующего отклонения
При этом каждая опора будет влиять на положение целевого знака относительно центра отверстия в зависимости от величины отклонения. Для определения результирующего отклонен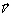
я необходимо выполнить алгебраическое суммирование отклонений по осям опор центроискателя – векто
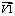ы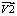 
, 
,
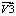. Координаты вершины векто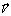
а будут определяться по следующим формула
м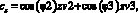
(
6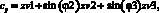
(
7)где φ2 – угол между осью ОХ и вектор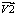
м ; φ3–угол между осью ОХ и вектор
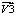м ; zv1, zv2 и zv3 – длины вектор
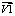в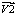 
, 
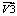и , взятые из массива ZV[…]. Dp – окружность, определяющая заданный допуск на точность работы центроискателя, радиус R – значение допуска
. Критерием годности исследуемой конструкции центроискателя является соблюдение неравенств
а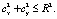
(
8)Неравенство (8) рекомендуется решать при условии наибольшего отклонения целевого знака центроискателя от центра отверстия (в наихудшем случае), когда одно замыкающее звено соответствует max значению из массива zam_zveno[…], другое – min значению, третье – их среднему значению. Если при данных условиях неравенство выполняется, то 100 % устройств будут соответствовать заданной точности
. Результаты исследования и их обсужден
иеВ качестве исходных данных были выбраны допуски на расположение отверстий реальных крупногабаритных объектов: турбина марки К-300-240-1 (допускаемое отклонение расточек под корпуса подшипников – не более 0,10 мм) и тепловозный дизельный двигатель марки 10Д100 (допускаемое отклонение опор подшипников – не более 0,05 мм) [1, 9
].Значение величины аср = 10,03 для допуска 0,10 мм, что соответствует 6 квалитету. Аналогичный расчет произведен при допуске в 0,05 мм, из которого следует, что составляющие звенья необходимо изготавливать по 5 квалитету. Значение замыкающего звена РЦ определено по рассчитанным квалитетам с использованием разработанной программы
. Расчет, исходя из взаимного влияния опор центроискателя, показывает, что условие (8) выполняется для допуска 0,05 мм при 6 квалитете, а для допуска 0,10 мм – при 7 квалитете соответственно. Результаты представлены в таблиц
Результаты расчетов
|
исследуемый механизм |
заданный допуск, мм |
для составляющих звеньев |
для замыкающего звена |
значение квалитета исходя из суммарного отклонения |
||
|
установленный квалитет |
среднее значение, мм |
верхнее отклонение, мм |
нижнее отклонение, мм |
|||
|
тепловозный двигатель 10Д100 |
0,05 |
5 |
0,034 |
+ 0,014 |
– 0,014 |
6 |
|
турбина К-300-240-1 |
0,10 |
6 |
0,051 |
+ 0,025 |
– 0,025 |
7 |
е.Заключен
иеРазработана математическая модель, которая позволяет оценить точность различных конструкций центроискателей отверстий деталей, как реальных, так и вновь проектируемых, а также оптимизировать допуски на размеры деталей центроискателей аналитическим расчетным методом. Составлен алгоритм и программа для расчета замыкающего звена РЦ по методу Монте-Карло. Проведенные численные исследования математической модели на реальных деталях показали эффективность ее использования для оценки точности центроискателе