При проведении исследования в рамках проекта РГНФ № 15-06-10765-а для выбора факторов, оказывающих наибольшее влияние на среднемесячные денежных доходы населения (тыс. руб. на душу населения), а также для выбора вида и побора параметров уравнения регрессии, используемого при оценке и прогнозировании, были выбраны процедуры кластерного и корреляционно-регрессионного анализа. Представленные процедуры часто реализуются как составные части многих пакетов прикладных программ для статистической обработки или анализа данных (пакеты Data mining). Для выполнения анализа и оценки в данном исследовании выбран пакет фирмы IBM SPSS Statistics версии 22 [8].
В качестве исходных данных выбраны отдельные показатели социально-экономического положения монопрофильных муниципальных образований (моногородов) Воронежской области за период с 2011 по 2015 г. – городские поселения, согласно распоряжению Правительства РФ № 1398-р [9], такие как г.п. Елань-Коленовское, г. Павловск, г. Россошь, г. Семилуки (данные официальных сайтов городских поселений, Федеральной службы государственной статистики [1, 4–7]) (см. табл. 1). Аналогично по остальным из перечисленных моногородам Воронежской области были составлены таблицы с показателями социально-экономического развития за период 2011–2015 гг.
Таблица 1
Показатели социально-экономического развития г. Россоши Воронежской области за период 2011–2015 гг.
|
№ п/п |
Показатель развития |
2011 |
2012 |
2013 |
2014 |
2015 |
|
1 |
Объем производства промышленных предприятий города (ОПППГ), млн руб. |
27972,00 |
33005,00 |
29877,00 |
32059,00 |
44430,00 |
|
2 |
Объем градообразующего предприятия (ОАО «Минудобрения») в объеме отгруженной продукции (ОГПОП), млн руб. |
24895,08 |
29603,10 |
26471,70 |
29173,70 |
40431,30 |
|
3 |
Инвестиции в основной капитал за счет муниципального бюджета (ИОКСМБ), млн руб. |
75,73 |
96,63 |
93,87 |
30,67 |
73,26 |
|
4 |
Оборот розничной торговли (ОРТ), млн руб. |
5686,00 |
6595,00 |
7714,00 |
8234,00 |
9743,00 |
|
5 |
Объем строительно-монтажных работ (ОСМР), млн руб. |
1683,00 |
1778,00 |
1708,00 |
1227,00 |
1300,00 |
|
6 |
Доходы местного бюджета (фактическое исполнение) (ДМБ), млн руб. |
328,64 |
334,67 |
401,14 |
348,52 |
549,37 |
|
7 |
Расходы местного бюджета (фактическое исполнение) (РМБ), млн руб. |
341,16 |
349,56 |
395,11 |
413,42 |
573,95 |
|
8 |
Численность населения занятого в экономике (ЧНЗВЭ), чел |
28000 |
27800 |
29080 |
27490 |
33390 |
|
9 |
Численность официально зарегистрированных безработных (ЧОЗБ), чел. |
168 |
174 |
90 |
155 |
203 |
|
10 |
Среднемесячные денежные доходы населения (СрДДН), тыс. руб. на душу населения |
17,35 |
18,70 |
18,15 |
19,24 |
25,21 |
Далее с помощью процедур кластерного анализа по полученным данным, за рассматриваемый период формируются группы показателей с аналогичной динамикой. Дается содержательная интерпретация по полученным группам, а на основе результатов кластеризации и корреляционного анализа осуществляется выбор факторов, которые наиболее подходят для анализа среднемесячных денежных доходов населения (тыс. руб. на душу населения). Таким образом, подбирается уравнение регрессии, которое позволит получить достоверные прогнозы среднемесячных денежных доходов населения и провести оценку прогноза данных доходов на 2016–2017 гг. Рассмотрим последовательное выполнение данных этапов в программном пакете IBM SPSS.
Исходные показатели в редакторе данных SPSS описываются на рабочем листе «Представление_Данные» (каждая ячейка хранит одно наблюдаемое значение переменной). Определение самих переменных проводиться во вкладке «Представление_Переменные» подробно можно рассмотреть в следующих источниках [2, 3, 10, 14]. Для выбора оптимального количества кластеров выполняется проведение предварительной классификации (меню «Анализ» команда «Классификация»/«Иерархическая кластеризация…» [11–13], в окне «Иерархический кластерный анализ» вводятся числовые переменные, которые соответствуют социально-экономическим показателям моногородов Воронежской области по годам, и помещаются в поле тестируемых переменных). В итоге для вывода обзора принадлежности, согласно которому определяется очередность построения кластеров и их оптимальное количество, получена обзорная таблица с порядком агломерации (см. табл. 2).
Таблица 2
Порядок агломерации (кластеров)
|
Этап |
Объединенный кластер |
Коэффициенты |
Этап первого появления кластера |
Следующий этап |
||
|
Кластер 1 |
Кластер 2 |
Кластер 1 |
Кластер 2 |
|||
|
1 |
6 |
7 |
5231,010 |
0 |
0 |
4 |
|
2 |
3 |
10 |
17654,893 |
0 |
0 |
3 |
|
3 |
3 |
9 |
74411,642 |
2 |
0 |
4 |
|
4 |
3 |
6 |
561459,575 |
3 |
1 |
5 |
|
5 |
3 |
5 |
9262713,359 |
4 |
0 |
8 |
|
6 |
1 |
2 |
56950986,166 |
0 |
0 |
7 |
|
7 |
1 |
8 |
121297528,543 |
6 |
0 |
9 |
|
8 |
3 |
4 |
267551200,159 |
5 |
0 |
9 |
|
9 |
1 |
3 |
4494181895,035 |
7 |
8 |
0 |
Из табл. 2 при определении оптимального количества кластеров решающее значение имеет показатель «Коэффициенты», подразумевает расстояние между двумя кластерами, определяемое на основе выбранной дистанционной меры. Оптимальное число кластеров равно разности количества наблюдений и номера шага, после которого происходит скачкообразное увеличение коэффициента. В нашем случае значительный скачок коэффициента происходит после 6 шага, это означает, что для данных, которые включают 10 наблюдений, оптимальным будет решение с 4 кластерами (10 – 6 = 4) [3].
Теперь для каждого наблюдения можно организовать вывод информации о принадлежности к кластеру (диалоговое окно «Иерархический кластерный анализ», по кнопке «Статистики…» задается принадлежность к кластерам – количество кластеров в нашем случае равно «4») [3, 11–13]. Также в данном окне предусмотрена возможность активирования диаграммы по кнопке «Графики…». По кнопке «Метод...» данного окна возможен выбор одного из методов, связанного с образованием кластеров, расчетом дистанционной меры и меры подобия [3]. В итоге согласно выставленным параметрам получили дендрограмму (рис. 1), визуализирующую процессы слияния, приведенные в табл. 2. При этом дендрограмма идентифицирует объединенные кластеры и значения коэффициентов на каждом шаге, отображаются не исходные значения коэффициентов, а приведенные к шкале от 0 до 25, а образованные слияния кластеров отображаются горизонтальными линиями (рис. 1).
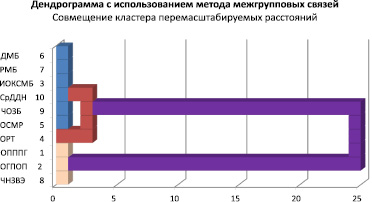
Рис. 1. Дендрограмма классификации показателей социально-экономического положения г. Россоши Воронежской области
Таким образом, независимо от выбора процедуры кластеризации показатели классифицируются одинаково. По результатам кластеризации первый кластер представлен 2-мя показателями: «ОПППГ, млн руб.»; «ОГПОП, млн руб.». Второй кластер представлен 6-ю показателями: «ИОКСМБ, млн руб.», «ОСМР, млн руб.», «ДМБ, млн руб.», «РМБ, млн руб.», «ЧОЗБ, чел.», «СрДДН, тыс. руб. на душу населения». Третий кластер представлен 1-м показателем «ОРТ, млн руб.». Четвертый кластер включает также 1 показатель – «ЧНЗВЭ, чел».
Для проведения содержательной интерпретации полученных кластеров необходимо разобраться в их значении. При этом помогут кластерные профили – распределенные согласно кластерной принадлежности средние значения переменных, которые включены в анализ (меню «Анализ» подгруппа «Сравнение средних» команда «Средние») [3]. В качестве результатов выводятся средние значения переменных (см. табл. 3).
Таблица 3
Отчет (среднее значение)
Показатели, представляющие 1 кластер, характеризуются устойчивым ростом средних значений в течение рассматриваемого периода (с 2011 г. по 2015 г.). Величины 3 и 4 кластера имеют схожий тренд с первым кластером. Второй кластер отличается самым низким по сравнению с другими уровнем средних значений, которые соответствуют параболической тенденции. При рассмотрении показателей социально-экономического положения г. Россоши наиболее интересным для анализа будет показатель «СрДДН, тыс. руб. на душу населения», который согласно классификации попал во 2-й кластер, состав представим в табл. 4.|
Кластер |
2011 г. |
2012 г. |
2013 г. |
2014 г. |
2015 г. |
|
1 |
26433,54 |
31304,05 |
28174,35 |
30616,35 |
42430,65 |
|
2 |
435,65 |
458,59 |
451,05 |
365,64 |
454,13 |
|
3 |
5686,00 |
6595,00 |
7714,00 |
8234,00 |
9743,00 |
|
4 |
28000,00 |
27800,00 |
29080,00 |
27490,00 |
33390,00 |
|
Всего |
8916,70 |
9975,47 |
9584,90 |
9915,06 |
13071,91 |
Таблица 4
Состав второго кластера
Далее в пакете SPSS изменяем исходные данные – оставляем показатели, входящие во второй кластер, при изменении столбцов и строк (строки – года исследуемого периода с 2011 по 2015 гг., столбцы показатели). Анализ направления и силы связи для каждой пары переменных в полученной группе проводится с помощью матрицы коэффициентов парной корреляции [12] (меню «Анализ» подгруппа «Корреляции»/«Парные…») [3]. В результате получится матрица коэффициентов парной корреляции (см. табл. 5).|
Год |
СрДДН, тыс. руб. на душу населения |
ИОКСМБ, млн руб. |
ОСМР, млн руб. |
ДМБ, млн руб. |
РМБ, млн руб. |
ЧОЗБ, чел. |
|
2011 |
17,35 |
75,73 |
1683,00 |
328,64 |
341,16 |
168 |
|
2012 |
18,70 |
96,63 |
1778,00 |
334,67 |
349,56 |
174 |
|
2013 |
18,15 |
93,87 |
1708,00 |
401,14 |
395,11 |
90 |
|
2014 |
19,24 |
30,67 |
1227,00 |
348,52 |
413,42 |
155 |
|
2015 |
25,21 |
73,26 |
1300,00 |
549,37 |
573,95 |
203 |
Таблица 5
Матрица коэффициентов парной корреляции (корреляция Пирсона)
|
СрДДН |
ИОКСМБ |
ОСМР |
ДМБ |
РМБ |
ЧОЗБ |
|
|
СрДДН |
1 |
-,126 |
-,627 |
,931* |
,970* |
,599 |
|
ИОКСМБ |
-,126 |
1 |
,842* |
,056 |
-,207 |
-,198 |
|
ОСМР |
-,627 |
,842* |
1 |
-,481 |
-,699 |
-,375 |
|
ДМБ |
,931* |
,056 |
-,481 |
1 |
,960** |
,326 |
|
РМБ |
,970* |
-,207 |
-,699 |
,960** |
1 |
,427 |
|
ЧОЗБ |
,599 |
-,198 |
-,375 |
,326 |
,427 |
1 |
Примечание.* Корреляция значима на уровне 0,05 (односторонняя).
Прямая тесная связь показателя СрДДН наблюдается со следующими величинами по порядку значимости: «РМБ» (коэффициент корреляции 0,970), «ДМБ» (корреляция 0,931). Из отчета SPSS видно, что наиболее статистически значима с вероятностью 93,1 % корреляция с показателем «ДМБ, млн руб.». Показатель «РМБ, млн руб.» приводит к ковариации с предыдущим показателем и им можно пренебречь. Далее для выполнения достоверного прогноза СрДДН составим уравнение регрессии (меню «Анализ»/ «Регрессия» выбирается «Линейная…») (проверено несколько комбинаций переменных и представлена наиболее подходящая). В табл. 6 приведен фрагмент регрессионного анализа.
Таблица 6
Фрагмент регрессионного анализа в SPSS (зависимая переменная СрДДН)
|
Модель |
Нестандартизованные коэффициенты |
Стандартизованные коэффициенты |
т |
Знач. |
||
|
B |
Ст. ошибка |
Бета |
||||
|
1 |
(Константа) |
7,293 |
2,884 |
2,529 |
,086 |
|
|
ДМБ |
,032 |
,007 |
,931 |
4,406 |
,022 |
|
Таким образом, наиболее подходящим оказалось линейное уравнение вида:
СрДДН = 7,293 + 0,032*ДМБ,
оно обладает хорошими качественными характеристиками (R2 = 0,931), статистически значимо вместе со своими параметрами. Прогноз СрДДН на 2016–2017 гг. (с вероятностью 90 %) представим в виде точечных и интервальных оценок (меню «Анализ»/«Прогнозирование» команда «Создать модели…», в окне «Конструктор моделей временных рядов»: вкладка «Переменные» указывается зависимая переменная – «СрДДН» и независимая переменная – «ДМБ»; вкладка «Параметры» указывается доверительный интервал – 90 %) [3]. Результаты соответствующих расчетов представлены в табл. 7.
Таблица 7
Результаты прогнозирования
|
Год |
ДМБ |
СрДДН |
Нижняя граница |
Верхняя граница |
|
2016 |
550,531 |
24,91 |
20,58 |
29,25 |
|
2017 |
608,969 |
26,78 |
22,45 |
31,12 |
График прогнозирования показателей, полученный в ходе выполнения указанных действий, представлен на рис. 2.
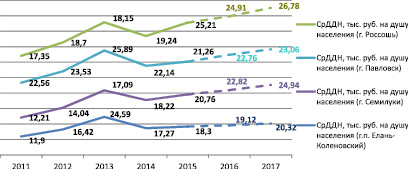
Рис. 2. График прогнозирования показателей моногородов Воронежской области
Таким образом, при увеличении в 2016–2017 гг. доходов местного бюджета возможно увеличение среднемесячных денежных доходов населения (СрДДН), тыс. руб. на душу населения. Исследуемые показатели социально-экономического развития г. Россоши за 2011–2015 гг. позволяют сделать вывод о такой возможности, если ситуация с градообразующим предприятием ОАО «Минудобрения» останется на прежнем уровне или не ухудшится (чего нельзя сказать о градообразующих предприятиях остальных представленных моногородов Воронежской области). Например, в г. Семилуки с 2013 г. на градообразующем предприятии ОАО «Семилукский огнеупорный завод» складывается сложная экономическая ситуация, которая приводит к решению о его ликвидации, при проведении анализа аналогичного данным г. Россошь. Наиболее подходящее линейное уравнение, для г. Семилуки: СрДДН = 21,708 – 0,029*ДМБ, оно также обладает хорошими качественными характеристиками (R2 = 0,674). Прогноз СрДДН на 2016–2017 гг. (с вероятностью 90 %) представим в виде точечных и интервальных оценок (рис. 2). В г. Павловск градообразующее предприятие ОАО «Павловскгранит» реорганизовано в два предприятия ОАО «Павловск Промвзрыв» и ОАО «Павловск Неруд». Наиболее подходящее линейное уравнение: СрДДН = 18,316 + 0,059*ДМБ, оно также обладает хорошими качественными характеристиками (R2 = 0,951). Прогноз СрДДН на 2016–2017 гг. (с вероятностью 90 %) представим в виде точечных и интервальных оценок (рис. 2). В г.п. Елань-Коленовском градообразующим предприятием является ОАО «Елань-Коленовский сахарный завод», которое также испытывает трудности с 2013 г. Наиболее подходящее линейное уравнение: СрДДН = 8,089 + 0,275*ДМБ, оно также обладает хорошими качественными характеристиками (R2 = 0,614). Прогноз СрДДН на 2016–2017 гг. (с вероятностью 90 %) представим в виде точечных и интервальных оценок (рис. 2).
Исследование выполнено при финансовой поддержке РГНФ в рамках научно-исследовательского проекта РГНФ № 15-06-10765-а.



