Известно, что предприятия отечественного авиационного двигателестроения выпускают газотурбинные установки (ГТУ) не только для авиации, но также построения электростанций различной мощности. Известно, что ГТУ является работоспособной лишь при наличии системы автоматического управления (САУ), поэтому задачам совершенствования САУ ГТУ уделяется серьезное внимание [4]. В ГТУ, предназначенных для электростанций, возникает необходимость обеспечения заданных показателей качества электроэнергии в условиях постоянно изменяющейся электрической нагрузки и изменения режимов работы электростанции, что увеличивает требования к САУ [8]. Исследуем использование адаптивного управления ГТУ с эталонной моделью и сигнальной настройкой для улучшения одного из важнейших показателей качества электроэнергии – частоты электрического тока синхронного генератора (СГ) [3]. Рассмотрение именно этого показателя качества электроэнергии связано с тем обстоятельством, что частота вращения свободной турбины ГТУ непосредственно преобразуется в частоту электрического тока синхронного генератора, работающего в автономном режиме, что, например, имеет место в условиях Дальнего Севера без связи с мощной электросистемой.
В качестве базы для построения рассматриваемых адаптивных систем возьмем методологический аппарат из работы [2], где с системных позиций рассматривается научно-техническая проблема создания адаптивных алгоритмов управления для электромеханических объектов с нелинейными свойствами. Так как в плане математического описания упрощенная линеаризованная модель двухвальной ГТУ и модель обобщенного электромеханического преобразователя из работы [2] подобны, имеются основания использовать положения работы [2] по отношению к новому объекту – ГТУ, работающей совместно с СГ. СГ здесь выступает в качестве нагрузки для ГТУ, но, одновременно и ГТУ оказывает сильное влияние на СГ, в результате образуется единая динамическая система ГТУ-СГ.
Газотурбинные электростанции
Важным и перспективным направлением развития отечественной энергетики является создание «умных» активно-адаптивных сетей электроснабжения, объединяющих разнородные генерирующие мощности: крупные и малые электростанции, возобновляемые и нетрадиционные источники электроснабжения. При этом по оценке специалистов всё более значительную роль будут играть газотурбинные электростанции мощностью до 25 МВт, создаваемые на базе авиационных газотурбинных установок (ГТУ). Такие ГТУ, преобразованные для наземной работы, часто называют конвертированными. Они вращают синхронные генераторы, вырабатывающие электроэнергию, поэтому именно они являются источником мощности газотурбинных электростанций [8].
Адаптивный подход
Использование обычных неадаптивных САУ приводит к большим срокам внедрения, затягиванию испытаний, трудностями в настройке и подстройке САУ ГТУ, такие системы оказываются достаточно жестко привязаны к конкретным условиям эксплуатации. В противоположность этому внедрение адаптивных систем позволяет даже при существенной нелинейности и нестационарности параметров улучшить показатели качества динамических характеристик, сократить сроки внедрения, облегчить наладку САУ и повысить их качество [2].
Моделирование синхронного генератора
Исследование адаптивного алгоритма управления будем проводить с помощью моделирования. Для этого требуются модели ГТУ и СГ.
Исследуемая модель синхронного генератора представлена на рис. 1. Генератор представлен блоком «СГ», на вход которого подаются вычисленные параметры синхронной машины, а также номинальный ток статора и номинальное напряжение статора [11].
На рис. 1 обозначено: Uf – напряжение обмотки возбуждения , Ud, Uq, – напряжение статора по осям d и q, id, iq – токи статора по осям d и q, if – ток возбуждения, iyd, iyq – токи демпферных обмоток, ω – электрическая скорость ротора, Rf – сопротивление обмотки возбуждения, Ryd, Ryd – сопротивление демпферных обмоток, Rs – сопротивление статора, ψf – потокосцепление обмотки возбуждения, ψd, ψq – потокосцепление для продольной d и поперечной q оси, ψyd, ψyq – потокосцепление демпферных обмоток, Ua, Ub, Uc – фазное напряжение по осям a,b,c.
Внутри блока «СГ» реализована структура синхронного генератора в соответствии с уравнениями (1–3) [3].
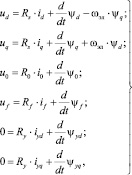 (1)
(1)
где
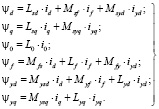 (2)
(2)
Электромагнитный момент запишется как
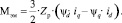 (3)
(3)
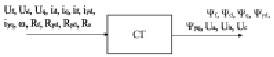
Рис. 1. Модель исследуемого СГ

Рис. 2. Структура нелинейной модели ГТУ
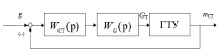
Рис. 3. Эталонная модель ГТУ
Быстрорешаемые линейные модели газотурбинных установок
Упрощенные быстрорешаемые модели ГТУ строятся на основе полученных экспериментальных данных [9]. ГТУ может быть работоспособна только при наличии системы автоматического управления (САУ), которая есть совокупность ГТУ и устройств управления [4]. Одним из мощных средств повышения эффективности САУ является создание так называемых «быстрорешаемых» или «быстросчетных» моделей ГТУ, полученных по результатам наблюдения за поведением реального объекта испытаний или его полной структурно сложной поэлементной модели [1, 9]. Идея быстрорешаемой модели [6] состоит в объединении линейной динамической модели и нелинейных статических характеристик ГТУ. Данный класс моделей позволяет обеспечить точность в границах 2–5 % [1]. Быстрорешаемые модели ГТУ, как правило, формируются по данным экспериментов с помощью алгоритмов идентификации [1]. Главное преимущество таких моделей – высокое быстродействие, поэтому такие модели иногда называют быстрорешаемыми или быстросчетными. Быстрорешаемые модели предназначены для использования в задачах диагностики, настройки и оптимизации систем управления ГТУ, в тренажерных комплексах, при стендовых испытаниях установок различного назначения: для электростанций, для газоперекачивающих агрегатов, для авиационного применения. Быстрорешаемые модели могут быть как линейными, так и нелинейными [1].
Модель для проведения исследования
Рассмотрим упрощенную динамическую модель ГТУ, полученную с помощью идентификации методом наименьших квадратов. Структура дифференциальных уравнений выбрана с учетом априорной информации об основных физических принципах преобразования энергии в ГТУ. Модель сохраняет допустимую адекватность для работы САУ ГТУ в режиме стабилизации частоты вращения свободной турбины ГТУ от холостого хода до 1,2 номинальной нагрузки. На рис. 2 изображена структурная схема полученной модели ГТУ [5, 7]:
а) уравнение ротора турбокомпрессора:
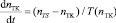 , (4)
, (4)
б) уравнение свободной турбины:
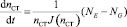 , (5)
, (5)
где nСТ – частота вращения свободной турбины; nTK – частота вращения ротора турбокомпрессора; nTS – установившаяся частота вращения ротора турбокомпрессора, взятая по нелинейной статической характеристике:
nTS = f(GT),
где GT – расход топлива; T(nTK) – постоянная времени турбокомпрессора, нелинейно зависящая от nTK, J(nCT) – момент инерции свободной турбины, нелинейно зависящий от nСТ; NE – мощность ГТУ; NG – мощность генератора (нагрузки).
Эталонная модель включает в себя, помимо частично линеаризованных уравнений (4) и (5), также регуляторы ГТУ. Регуляторы включаются последовательно (рис. 3). Передаточная функция регулятора nСТ имеет следующий вид [10]:
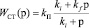 , (6)
, (6)
передаточная функция регулятора дозатора газа WG(p)
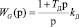 . (7)
. (7)
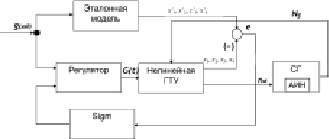
Рис. 4. Адаптивная система регулирования с сигнальной настройкой
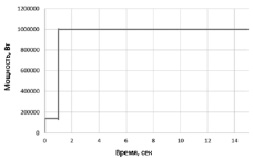
Рис. 5. Активная мощность генератора
Параметры частично линеаризованной эталонной модели ГТУ приняты следующими (для ГТУ мощностью 6 МВТ): T(nTK) = 0,8 = const; J(nCT) = 1,64 = const; nTS = f(GT) – нелинейная зависимость, NE = f(nTK) – нелинейная зависимость; Тогда параметры регуляторов (6) и (7) с Tμ = 0,1 (малой некомпенсированной постоянной времени) будут следующими: TД = 2; kД = 0,5; kf = 2; ki = 10; kП = 5,67. Сигнал задания g = ( ) = 6925 об/мин.
) = 6925 об/мин.
Сигнальная настройка по четырем переменным
Проведем по полученным параметрам регулятора (6,7) адаптивную сигнальную настройку по схеме, изображенной на рис. 4, где АИН – активно-индуктивная нагрузка, Sigm – сигмоидальная функция [6].
Эталонная модель (ЭМ) линеаризована вблизи точки номинального режима.
Переменные модели
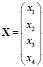 ,
,
где x1 = nst, x2 = ntk, x3 – выход интегратора регулятора дозатора газа, x4 – выход интегратора регулятора свободной турбины.
Тогда матрица коэффициентов ЭМ
 .
.
Матрица управления ЭМ
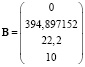 .
.
Из уравнения
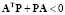 (8)
(8)
находим матрицу P.
Для этого вначале задаемся отрицательно-определенной матрицей Q, ее лучше брать диагональной:
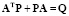 . (9)
. (9)
В зависимости от выбора матрицы Q матрица P и результат сигнальной настройки будет разным. По результатам экспериментов была выбрана следующая матрица:
Q = diag (– 0,1 – 1 – 10 – 100).
В результате матрица P имеет следующий вид:
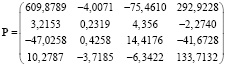 ,
,
и сигнальный (5) алгоритм получается в следующем виде
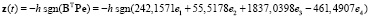 .
.
Рис. 6. Частота вращения свободной турбины. 1 – эталонная модель, 2 – нелинейная модель без адаптации, 3 – нелинейная модель с сигнальной настройкой
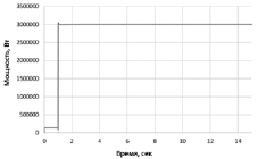
Рис. 7. Активная мощность генератора
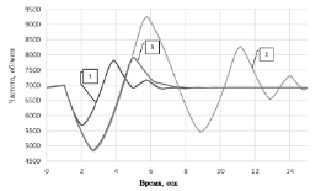
Рис. 8. Частота вращения свободной турбины. 1 – эталонная модель, 2 – нелинейная модель без адаптации, 3 – нелинейная модель с сигнальной настройкой
Динамические показатели регулирования по частоте вращения свободной турбины nCT
|
Величина нагрузки, МВт, (наброс мощности) |
Система |
Максимальное отклонение nCT, % |
Время переход. процесса, с |
Число колебаний |
Стат. ошибка, % |
|
1 |
Эталонная |
4,84 |
6,65 |
2 |
0 |
|
Без адаптации |
7,03 |
41,32 |
8 |
0 |
|
|
С адаптацией |
5,5,8282 |
6,78 |
2 |
0 |
|
|
3 |
Эталонная |
1717,9393 |
5,35 |
2 |
0 |
|
Без адаптации |
3030,31,31 |
24,54 |
4 |
0 |
|
|
С адаптацией |
2929,6767 |
6,55 |
2 |
0 |
Объединим модели ГТУ и СГ, проведем серию экспериментов при изменении нагрузки генератора c 140 кВт (холостой ход) до 1 МВт (рис. 5, 6), и с 140 кВт до 3 МВт (рис. 7, 8). При этом генератор работает в автономном режиме на выделенную активно-индуктивную нагрузку. Для изменения мощности генератора изменяют сопротивления активно-индуктивной нагрузки. Поэтому мощность генератора не изменяется скачком, а наблюдается некоторый переходный процесс изменения активной мощности СГ (рис. 5, 7).
Результаты сравнительного анализа
Как видно из таблицы, частота вращения свободной турбины частично линеаризованной эталонной модели и нелинейной модели с адаптивным управлением значительно более близки, чем у нелинейной модели без адаптивного управления. Таким образом, за счет адаптивного управления система приближается к эталонному поведению. При этом нелинейная модель без адаптации подвержена слабозатухающим колебаниям.
Заключение
Таким образом, в результате исследований показана принципиальная возможность улучшения показателей переходного процесса по частоте вращения свободной турбины за счет применения адаптивного управления, при этом качество переходных процессов по напряжению не ухудшается. Адаптивный алгоритм управления исследован при совместном моделировании ГТУ и СГ. В результате применения адаптивного управления с сигнальной настройкой достигнуто улучшение динамических показателей регулирования частоты по максимальному отклонению на 11,21 %, по длительности переход процесса на 81,15 %.



