Приводы механизмов, выполняющих в современных высокоскоростных машинах-автоматах операции транспортировки, включают в себя, как правило, кулачковые механизмы, позволяющие реализовать движение выходного звена по схеме «прямой ход – выстой – обратный ход – выстой» [1, 2, 4, 7, 9]. Очевидна взаимосвязь эффективности конструкции механизма с такими его параметрами, как кинематические характеристики, в числе которых закон профилирования дорожек кулачков и точность его исполнения, упруго-инерционные свойства звеньев механизма и его соединений, скорость работы, внешние нагрузки [1, 2, 4–10]. В статье предлагается методика оценки влияния погрешности, возникающей при изготовлении дорожек кулачков, на уровень динамических процессов в механизме.
Очевидно, что функция искажения профиля носит случайный характер и на практике, для уже готового кулачка, может быть получена путём измерений. Но такой подход теряет смысл при динамических исследованиях механизма на этапе его проектирования. По мнению авторов данной работы, задача исследования динамики механизма с учётом погрешности изготовления профиля кулачка состоит в определении таких характеристик изменения функции искажения, в пределах допусков на изготовление кулачка, при которых уровень динамических процессов в механизме достигает максимума. Это даёт возможность получить ещё один (кроме допуска на изготовление) критерий выбраковки кулачков, а также реализовать алгоритм исследования колебательных процессов в механизме с кулачками, профиль которых изготовлен с заданной погрешностью.
Представим погрешность изготовления кулачка в виде функции искажения его профиля χ = χ(φ0). Тогда действительный профиль кулачка
. (1)
В выражении (1) φ0 – угол поворота кулачка, 
– функция, описывающая идеальный профиль его дорожки, χ(α) – гармоническая функция изменения погрешности:
, (2)
где χmax – величина поля допуска радиус-векторов действительного профиля кулачка, соответствующая обычно IT6 – IT8 (по ЕСДП СЭВ), χ0 – смещение поля допуска, относительно номинального размера (например, если поле допуска h7, то χ0 = –IT7/2), k – параметр, определяющий характер изменения функции искажения.
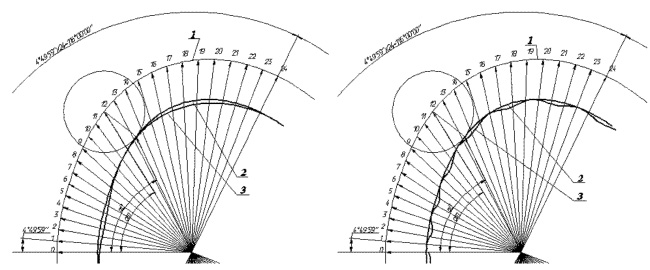
На рис. 1 показаны возможные отклонения профиля от идеального при различных значениях k для кулачка прямого хода привода механизма переноса ХВА АВ1818 [4, 9]. Поле допуска профиля кулачка соответствует h7 (от 0 до – 40 микрон), но на рисунке увеличено, для наглядности, в 100 раз.
а б
Рис. 1. Фрагмент чертежа профиля кулачка прямого хода механизма переноса ХВА АВ1818: а – действительный профиль при k = 5, б – при k = 20. 1 – теоретический профиль, 2 – действительный идеальный профиль, 3 – действительный профиль с учётом погрешности
Таким образом, задача исследования найти значения коэффициента k, при которых наблюдается резкий рост динамических процессов в механизме при работе его с различной производительностью. Выяснить, в какой степени влияет на динамику механизма погрешность изготовления дорожки кулачка при различных законах его профилирования.
Интенсивность динамических процессов в механизмах холодновысадочных автоматов на временном отрезке 0 ≤ t ≥ T можно оценить на основании следующих критериев [4, 5]:
1. Точность и среднеквадратичное значение точности позиционирования исполнительного звена:
, (3)
. (4)
2. Максимальное значение ускорения исполнительного звена механизма:
. (5)
3. Максимальное и среднеквадратичное отклонения ускорения исполнительного звена механизма от идеальных значений:
. (6)
. (7)
4. Максимальные и среднеквадратичные нагрузки в звеньях механизма:
(8)
. (9)
В формулах (3) – (7) xn и 
, 
и 
соответственно реальное и идеальное (без учёта упругости звеньев, точности их изготовления и зазоров в кинематических парах) перемещение и ускорение исполнительного (n-го) звена механизма. Предполагается, что это звено движется поступательно. Qi(t) в выражениях (8), (9) – нагрузка в i-м звене механизма, которую можно найти как произведение его жёсткости на деформацию.
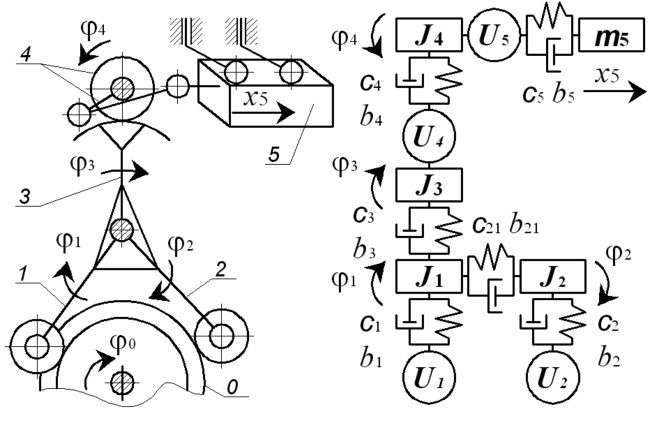
На рис. 2, а показан привод системы переноса заготовок между штамповочными позициями ХВА 1818, на рис. 2, б его динамическая модель. Принципы, положенные в основу построения динамической модели и её математического описания (10), приведены в работах [4, 5 – 10]. При разработке программного решения [3] использованы методы технологии компонентного моделирования и объектно-ориентированных технологий [6, 9]. Для расчёта упруго-инерционных параметров применены методы твердотельного моделирования [8].
а б
Рис. 2. Кулачково-рычажный привод механизма переноса ХВА 1818 (а) и его динамическая модель (б): 0 – блок кулаков; 1 – рычаг прямого хода; 2 – рычаг обратного хода; 3 – верхнее плечо рычага прямого хода с зубчатым сектором; 4 – кривошип с зубчатым колесом; 5 – каретка переноса
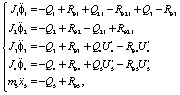(10)
В уравнениях (10) нагрузки и силы диссипации энергии в звеньях механизма и его кинематических парах:
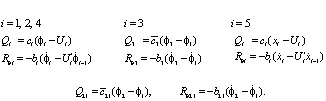(11)
Коэффициенты жёсткости звеньев с учётом зазоров в кинематических парах:
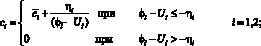
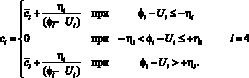; (12)
.
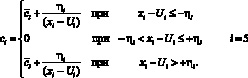Здесь ηi – односторонний зазор в соединении звеньев механизма, 
– жёсткость соответствующего звена, bi – коэффициент диссипации энергии [4].
Не всегда при исследовании динамики механизма есть смысл одновременно применять все приведённые выше критерии. Однако их минимальный набор должен включать, если речь идет об исследовании колебательных процессов в механизме, величины, содержащие среднеквадратичное значение какого-либо кинематического параметра и, возможно, – его максимальное значение. В данном конкретном случае в качестве такого параметра выбрано изменение ускорения исполнительного звена (каретки переноса).
Динамические исследования привода механизма переноса проводились в системе dam [3–7, 9] в предположении, что размеры его элементов лежат в пределах допусков на изготовление, то есть их износ минимален, а скорость вращения ведущего звена (кулачков) постоянна.
На рис. 3 показано, как выглядят функции 
и 
на участке прямого хода и верхнего выстоя при различных значениях параметра k в выражении погрешности профиля (2). Дорожка кулачка на участке подъёма спрофилирована по симметричному синусоидальному закону изменения ускорения. Скорость вращения кулачков 100 оборотов в минуту.
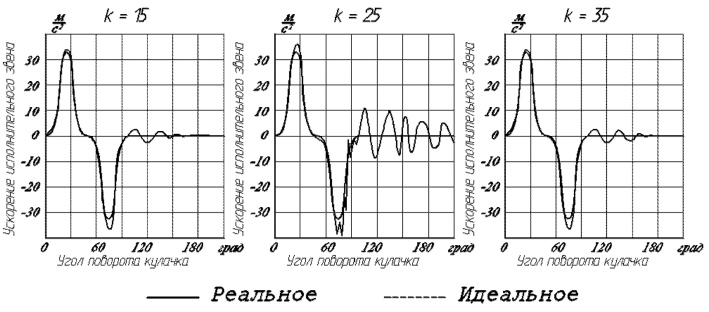
Рис. 3. Ускорение (реальное и идеальное) каретки переноса ХВА АВ1818 при различных значениях параметра k
Как следует из анализа данных, приведённых на рис. 3, характер изменения функции погрешности χ может оказать существенное влияние на динамические процессы, протекающие в механизме, и при определённых значениях частот её гармоник привести к резкому росту последних.
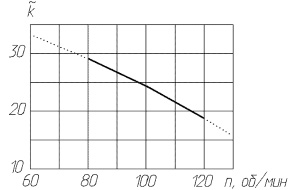
Рис. 5. Зависимость критической частоты функции погрешности дорожки кулачка от скорости его вращения
Результаты оценки уровня динамических процессов в приводе механизма переноса заготовок с помощью критерия (6) – среднеквадратичного отклонения значения реального ускорения исполнительного звена от идеального представлены на рис. 4. Если обозначить через 
значение k, при котором функция 
достигает максимума, а через n скорость вращения кулачков, то зависимость 
окажется близкой к линейно убывающей (рис. 5) и практически не зависящей от закона профилирования кулачков.
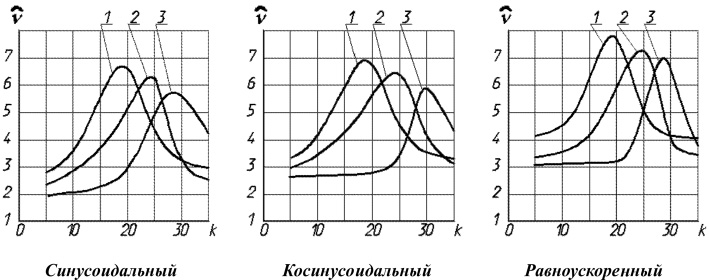
Рис. 4. Значения среднеквадратичного отклонения реального ускорения каретки переноса ХВА АВ1818 от идеального при различных законах профилирования кулачков и различной скорости их вращения: 1–120 об./мин, 2–100 об./мин, 3–80 об./мин
Анализ этой зависимости позволяет определить зону критических значений параметра k функции погрешности дорожки кулачка для заданного скоростного интервала эксплуатации оборудования. Так для кулачков системы переноса ХВА АВ 1818 частота функции погрешности χ не должна лежать в пределах от 10 до 35 при работе автомата с паспортной производительностью.