С 1 января 2016 года в России в силу вступит новый криптографический стандарт ГОСТ Р 34.12-2015 «Информационная технология. Криптографическая защита информации. Блочные шифры» [5]. В его состав войдут два алгоритма шифрования: ныне действующий стандарт шифрования ГОСТ 28147-89 и новый блочный алгоритм шифрования Кузнечик. В составе нового стандарта действующий алгоритм шифрования ГОСТ 28147-89 именуется как Магма.
В настоящей статье предлагается рассмотреть возможные походы к анализу этих двух шифров с использованием метода слайдового анализа. Слайдовая атака (SlideAttacks) была предложена в 1999 году Алексом Бирюковым и Дэвидом Вагнером [1]. Этот метод анализа применим ко всем алгоритмам блочного шифрования и не зависит от числа раундов шифрования. Алгоритм может обладать самоподобием за счет периодического использования секретного ключа, что возможно в случае использования слабой функции выработки раундовых подключей. Поэтому анализ составной части шифра, отвечающей за выработку раундовых подключей, является важной частью анализа. Основная идея слайдовой атаки заключается в том, что можно сопоставить один процесс зашифрования с другим таким образом, что один из процессов будет «отставать» от другого на один раунд. Тогда, в случае успешного нахождения такой пары текстов, можно извлечь информацию о битах секретного ключа, проанализировав первый и последний раунды шифрования. Подробнее о применении слайдовой атаки можно прочесть в работе [1–4].
Так как для алгоритма Магма (n = 64) не предусмотрена функция выработки раундовых подключей, то мы предлагаем рассмотреть варианты, которые будут значительным образом ослаблять стойкость этого алгоритма. Рассмотрим случай, когда в алгоритме Магма все восемь раундовых подключей примут одно и то же значение. Так как один раундовый подключ имеет длину 32 бита, то всего таких комбинаций для различных значений секретного ключа может быть 232 от общего объема ключевого пространства 2256. При такой длине ключа перебор всех комбинаций ключевого пространства составит всего 232. А при применении слайдовой атаки это значение может сократится до 216 с ожиданием успеха р = 0,5 согласно парадоксу Дней Рождений.
Сопоставим два процесса зашифрования друг против друга с запаздыванием на один раунд так, как показано на рис. 1.
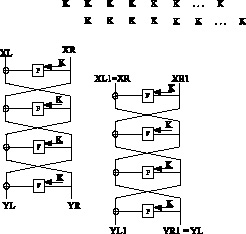
Рис. 1. Анализ шифра Магма с запаздыванием на 1 раунд
Так как алгоритм Магма построен по схеме Фейстеля, а мы предполагаем, что второй открытый текст является выходом первого раунда шифрования первого текста, то получаем следующий критерий отбора: XL1 = XR;YR1 = YL.
Алгоритм поиска слайдовой пары будет сводиться к следующим действиям:
Алгоритм 1
1. Зафиксировать первый текст Х и соответствующий ему шифр Y.
2. Зафиксировать левую часть второго текста XL1 = XR.
3. Предположить правую часть второго текста XR1.
4. Получить шифр Y1
5. Если YR1 = YL, то вычислить ключ, иначе вернуться к шагу 3.
Так как перебор значений ведется только по правой половине блока XR1, которая может принимать одно из 232 значений, то согласно парадоксу Дней Рождений, нам будет достаточно перебрать 216 текстов для того, чтобы найти слайдовую пару с вероятностью успеха р = 0,5. Важно отметить, что эта и последующие рассматриваемые атаки будут работать при любом заполнении S-блоков, в том числе и для блоков, утвержденных для алгоритма Магма.
Теперь рассмотрим случай, когда в алгоритме Магма циклически повторяются два раундовых подключа и не меняют порядок следования в последних раундах шифрования.Это начальное допущение легко позволит выполнить слайдовую атаку. Но при этом важно помнить, что в оригинальном шифре Магма раундовые подключи меняют свой порядок следования. Таких комбинаций для различных значений двух ключей может быть 264 от общего объема ключевого пространства 2256. При такой длине ключа перебор всех комбинаций составит всего 264. А при применении слайдовой атаки это значение сократится до 232.
Сопоставим два процесса зашифрования друг против друга с запаздыванием на два раунда так, как показано на рис. 2.
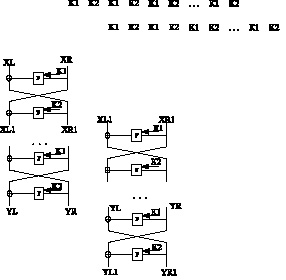
Рис. 2. Анализ шифра Магма с запаздыванием на 2 раунда
В этом случае мы предполагаем, что второй открытый текст является выходом второго раунда шифрования первого текста. Рассмотрим, как связаны между собой первый открытый текст (XL, XR) и второй открытый текст (XL1, XR1):
XR⊕ XL1 = F(XR, K1); (1)
XL1 ⊕XR = F(XR1, K2); (2)
Аналогичным образом определим, как связаны между собой шифры для первого (YL, YR) и второго текстов (YL1, YR1):
YL1 ⊕ YR = F(YR1, K2); (3)
YL ⊕ YR1 = F(YR, K1). (4)
Алгоритм поиска слайдовой пары c одновременным нахождением ключа будет сводиться к следующим действиям:
Алгоритм 2
1. Зафиксировать первый текст Х и соответствующий ему шифр Y.
2. Предположить второй текст Х1 и получить соответствующий ему шифр Y1.
3. Из формулы (1) вычислить значение К1.
4. Подставить найденное значение в формулу (4). Если равенство не выполняется, то вернуться к шагу 2.
5. Из формулы (2) вычислить значение К2.
6. Подставить найденное значение в формулу (3). Если равенство не выполняется, то вернуться к шагу 2.
7. Если оба равенства в формулах (4) и (3) выполняются, то мы нашли слайдовую пару и определили используемый секретный ключ.
Согласно парадоксу Дней Рождений, нам будет достаточно перебрать 232 текстов для того, чтобы найти слайдовую пару с вероятностью успеха р = 0,5.
Теперь рассмотрим случай, когда в алгоритме ГОСТ циклически повторяются четыре раундовых подключа К1 – К4 и не меняют порядок следования в последних раундах шифрования. Таких комбинаций для различных значений двух ключей может быть 2128 от общего объема ключевого пространства 2256. При такой длине ключа перебор всех комбинаций составит всего 2128. А при применении слайдовой атаки это значение сократится до 265.
Сопоставим два процесса зашифрования друг против друга с запаздыванием на четыре раунда так, как показано на рис. 3.
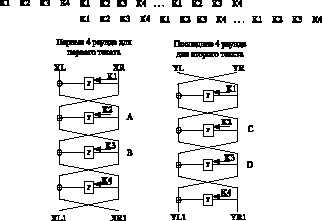
Рис. 3. Анализ шифра Магма с запаздыванием на 4 раунда
На рис. 3 показаны слева первые четыре раунда для преобразования первого текста и справа четыре последних раунда для преобразования второго текста. Также рис. 3 отражает взаимосвязь между первым открытым текстом (XL, XR) и вторым открытым текстом (XL1, XR1), а также между первым шифром (YL, YR) и вторым (YL1, YR1). На рис. 3 введены промежуточные значения A, B, C, D, которые отражают входы, поступающие на функцию F для второго и третьего раундов. В соответствии с рис. 3 можно выявить следующие связи для промежуточных значений:
A = XL ⊕ F(XR, K1); (5)
B = XR1 ⊕ F(XL1, K4); (6)
C = YR ⊕ F(YL, K1); (7)
D = YL1 ⊕ F(YR1, K4); (8)
A ⊕ XL1 = F(B, K3); (9)
C ⊕ YR1 = F(D, K3). (10)
Алгоритм будет заключаться в следующем. Для каждой потенциальной слайдовой пары мы будем строить таблицы для всех возможных значений К1 и для всех возможных значений К4. Итого две таблицы по 232 значений каждая. Пробегая по таблицам будем смотреть, даст ли какая-нибудь комбинация К1 и К4 такие значения A, B, C, D, что будут выполнены равенства (9) и (10). Если равенства (9) и (10) будут выполнены, то это даст нам информацию о значениях ключей К1 и К2. Отсюда легко можно будет найти значение подключей К3 и К4. Согласно парадоксу Дней Рождений, нам будет достаточно перебрать 232 текстов для того, чтобы найти слайдовую пару с вероятностью успеха р = 0,5. При этом для каждой потенциальной слайдовой пары необходимо будет сделать 233 опробований (2 таблицы по 232). Таким образом, общая сложность анализа составит 265 опробований.
Алгоритм поиска слайдовой пары c одновременным нахождением подключей будет сводиться к следующим действиям:
Алгоритм 3
1. Зафиксировать первый текст Х и соответствующий ему шифр Y.
2. Предположить второй текст Х1 и получить соответствующий ему шифр Y1.
3. Из формул (5) и (6) вычислить значения А и В для всех значений К1.
4. Из формул (7) и (8) вычислить значения С и D для всех значений К4.
5. Для всех значений (А, В) предположить значение К3 из формулы (9).
6. Для всех значений (С, D) предположить значение К3 из формулы (10).
7. Если значения К3 из п. 5 не совпадают со значениями К3 из п.6, то вернуться к шагу 2.
8. Из найденных значений K1, K2, K3 вычислить раундовый подключ K4.
Теперь рассмотрим вариант применения слайдовой атаки к анализу алгоритма Кузнечик. Для этого прежде всего оговорим рассматриваемые допущения. В алгоритме Кузнечик используется функция выработки раундовых подключей, построенная по схеме Фейстеля. Основываясь на этом, для оригинального шифра можно показать, что единственно потенциально возможным случаем повторения раундовых подключей является вариант, когда ключи будут циклически повторяться 1 по 5. Остальные варианты выработки одинаковых циклических ключей невозможны. Тем не менее мы рассмотрим случаи для вариантов Кузнечика с повторяющимися раундовыми ключами с тем, чтобы в дальнейшем можно было понять, как перейти от простых вариантов анализа к более сложным. В случае с одним, циклически повторяющимся раундовым ключом, сопоставим два процесса зашифрования с запаздыванием на один раунд так, как показано на рис. 4.
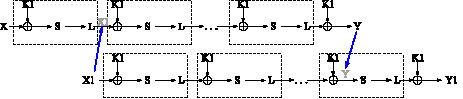
Рис. 4. Анализ шифра Кузнечик с запаздыванием на 1 раунд
Тогда выход первого раунда зашифрования первого текста Х будет являться входным значением Х1 второго процесса зашифрования. Точно также выходное зашифрованное значение Y будет являться промежуточным значением второго процесса зашифрования перед последним преобразованием S. Рассмотрим условия поиска слайдовых пар. Для этого определим, каким соотношением должны быть связаны значения X1 и Х. Согласно схеме, мы ожидаем, что Х1 будет выходом первого раунда зашифрования значения Х, тогда
Х ⊕ K1 = S-1(L-1(X1)). (11)
Аналогичным образом рассмотрим, каким соотношением связаны значения выходов Y и Y1. Мы ожидаем, что значение Y поступает на вход последнего преобразования S. Тогда
Y1 ⊕ K1 = L(S(Y)). (12)
Из формул (11) и (12) получаем, что
K1 = Х⊕ S-1(L-1(X1)), (13)
K1 = Y1 ⊕L(S(Y)). (14)
Так как в каждом раунде используется один и тот же раундовый подключ, то, объединив выражения (13) и (14), получаем условие отбора слайдовых пар
Х ⊕ S-1(L-1(X1)) = Y1 ⊕L(S(Y)) (15)
Вопрос только в том, сколько текстов нам придется перебрать, прежде чем мы найдем хотя бы одну такую слайдовую пару. Согласно парадоксу Дней Рождений, при переборе 264 разных текстов нас может ожидать успех с вероятностью р = 0,5.
Теперь рассмотрим случай, когда циклически повторяются два раундовых подключа (рис. 5).

Рис. 5. Анализ шифра Кузнечик с запаздыванием на 2 раунда
Необходимо сопоставить два процесса зашифрования, но с запаздыванием на два раунда. Тогда выход второго раунда зашифрования первого текста Х будет являться входным значением Х1 второго процесса зашифрования. Точно так же выходное зашифрованное значение Y будет являться промежуточным значением второго процесса зашифрования перед предпоследним преобразованием S. Рассмотрим условия поиска слайдовых пар. Для этого определим, каким соотношением должны быть связаны значения X1 и Х. Согласно схеме, мы ожидаем, что Х1 будет выходом второго раунда зашифрования значения Х, тогда
Х ⊕ K1 = S-1(L-1(S-1(L-1(X1)) ⊕ K2)). (16)
Аналогичным образом рассмотрим, каким соотношением связаны значения выходов Y и Y1. Мы ожидаем, что значение Y поступает на вход предпоследнего преобразования S. Тогда
L(S(Y)) ⊕ K1 = S-1(L-1(Y1⊕ K2)). (17)
Из формул (16) и (17) получаем, что
K1 = Х⊕ S-1(L-1(S-1(L-1(X1)) ⊕ K2)), (18)
K1 = L(S(Y)) ⊕S-1(L-1(Y1⊕ K2)). (19)
Так как для обоих процессов зашифрования значение К1 будет одним и тем же, то, объединив выражения (8) и (9) получаем следующее соотношение:
Х⊕ S-1(L-1(S-1(L-1(X1)) ⊕ K2)) = = L(S(Y)) ⊕S-1(L-1(Y1⊕ K2)). (20)
В выражении (20) присутствует неизвестный нам ключ К2. Поэтому для каждой пары значений (Х, Y); (X1, Y1) необходимо будет перебирать все возможные варианты ключа К2. Если равенство (20) выполнится, то это будет искомая слайдовая пара и ключ К2, а значение ключа К1 можно будет легко восстановить по формулам (18), (19). Согласно парадоксу Дней Рождений, для нахождения правильной слайдовой пары с вероятностью успеха р = 0,5, нам понадобится перебрать 264*2128 = 2192 различных текстов, что значительно меньше объема полного перебора 2256.
Работа выполнена при поддержке гранта РФФИ № 15-37-20007-мол-а-вед.



