Введение
Применение современных IT-технологий практически во всех сферах человеческой деятельности привело к ситуации, когда вопросы обеспечения защиты данных от несанкционированного доступа (НСД) становятся обязательными при построении информационных систем. При этом очевидно, что дальнейшее увеличение объемов хранимой и передаваемой информации приводит к наращиванию потенциальных возможностей злоумышленника по НСД к информационной сфере. Решить данную задачу можно только на основе комплексного подхода.
Одним из направлений обеспечения требуемого уровня защиты информации от НСД является использование схем разделения секрета. Применение таких схемы позволяет определенной группе пользователей восстановить секретный ключ из его образов при работе в многопользовательской информационной системе.
Решение задачи
Несмотря на многообразие схем разделения секретного ключа на секретные доли, все они решают задачу сохранения ключевых данных от НСД, которые при определенных условиях будут восстановлены и использованы в системеобработки и передачи данных. При этом схемы построены таким образом, что ни один абонент группы не сможет вычислить пароль без помощи других абонентов группы.
Рассматривая различные схемы разделения секрета можно отметить, что они состоят из двух взаимосвязанных протоколов:
- протокола формирования и распределения долей секрета между абонентами;
- протокола восстановления секрета группой пользователей с помощью их секретных долей.
В основу первого протокола положен алгоритм действий системы и пользователей, в результате которых каждый авторизованный абонент получает свою долю секретного ключа. Второй протокол применяется для того, чтобы законные пользователи, собравшись вместе и объединив свои секретные доли, могли восстановить секретный ключ.
Рассмотрим модулярную схему разделения секрета и проведем ее реализациюв полиномиальной системе классов вычетов (ПСКВ). В данной алгебраической системе в качестве модулей используются неприводимые полиномы pi(z). Благодаря своим особенностям полиномиальная система классов вычетов в настоящее время может быть использована в системах цифровой обработки сигналов, при построении систем криптографической защиты данных [1-6], а также для реализации процедур поиска и коррекции ошибок [8,9]. Следует отметить, что полиномиальная система классов вычетов может быть положена в основуалгоритма работы пороговой схемы(t, N) разделения секрета. Для реализации (t, N)-пороговой схемы разделения секрета выбирается неприводимые полиномы удовлетворяющие условию
.(1)
Затем определяется полином px(z), такой что
, (2)
гдеi=1, 2, …, n.
Данный полином определяет максимальное количество разрядов секретного ключаM(z) согласно
, (3)
где M(z) - полиномиальную форму секретного ключа.
С целью обеспечения правильной работы схемы разделения секрета, использующего (t, N)-пороговую схему, представленную в ПСКВ,осуществляется проверка
. (4)
Так как делить секретный ключ на отдельные части и распределять его пользователям нельзя, то в алгоритме предлагается провести «затемнение секрета», используя выражение
. (5)
где r(z) – полном, выбираемый для затемнения секрета.
Затем затемненный образ секрета делится на части согласно
. (6)
и в виде долейраспределяется между абонентами группы.Кроме долей образа M*(z) пользователям по закрытому каналу рассылаются значение полиномов pi(z),r(z) иpx(z).Таким образом, каждый член группы получает свои данные, с помощью которых группа сможет восстановить секрет.
Для восстановления зашумленного образа секрета M*(z) необходимо наличие, как минимум, tпользователей, которые применяют китайскую теорему об остатках, в соответствии
, (7)
где 
- i-й ортогональный базис в системе, состоящей из t пользователей; Pt(z) - полный диапазон, определяемый основаниями t пользователей.
При этом данный диапазон задается набором оснований согласно
. (8)
Используя выражения (7) и (8), t и более пользователей способны восстановить M*(z), а затем, зная r(z) и px(z), определить секрет M(z).
Однако, как показывает анализ работ [1,7,10], вычисление значения ортогонального базиса для динамически меняющегося набора пользователей группы является довольно сложной задачей. Решить данную задачу можно только на основе алгоритма, позволяющего эффективно осуществить процедуру пересчета ортогональных базисов.Для получения ортогонального базиса необходимо знать Pt(z) - полный диапазон, определяемый основаниями t пользователей. Тогда
, (9)
где mj(z) –вес ортогонального базиса j –го основания
Именно вычисление значения веса ортогонального базиса является наиболее сложно операцией. Известно [7], что использование mj(z) позволяет обеспечить выполнение условия
. (10)
Подставим равенства (8) и (10) в выражение (9). Тогда получаем
. (11)
Воспользуемся равенством (11) и выражением (10). В этом случаеимеем
. (12)
Разделив обе части равенства (5.6) на величину
получаем
. (13)
Принимая во внимание попарную простоту модулей ПСКВ, имеем
. (14)
Тогда значение веса ортогонального базиса будет определяться
. (15)
Таким образом, очевидно, что величина веса ортогонального базиса определяется произведением величин обратных основаниям pi(z) по модулю pj(z). Рассмотренный выше алгоритм вычисления значений ортогонального базиса ПСКВ представлен в работе[7]. В таблице 1 представлены значения mij(z) для модулей ПСКВ p1(z)=z+1; p2(z)=z2+z+1;p3(z)=z4+z3+z2+z1+1; p4(z)=z4+z3+1; p5(z)=z4+z+1.
Таблица 1
Величины mij(z) для поля GF(24).
|
Значение рi(z) основания ПСКВ |
|||||
|
p1(z) |
p2(z) |
p3(z) |
p4(z) |
p5(z) |
|
|
mi1(z) |
- |
1 |
1 |
1 |
1 |
|
mi2(z) |
z |
- |
z |
z+1 |
1 |
|
mi3(z) |
z3+z |
z3+1 |
- |
z2+1 |
z3+z2+1 |
|
mi4(z) |
z3 |
z3+z2+z |
z2 |
- |
z3+z+1 |
|
mi5(z) |
z3+z2+z |
z2+z |
z3+z |
z3+z2 |
- |
На рисунке 1 показана структура устройства вычисления ортогонального базиса для схемы разделения секрета, функционирующего в ПСКВ.
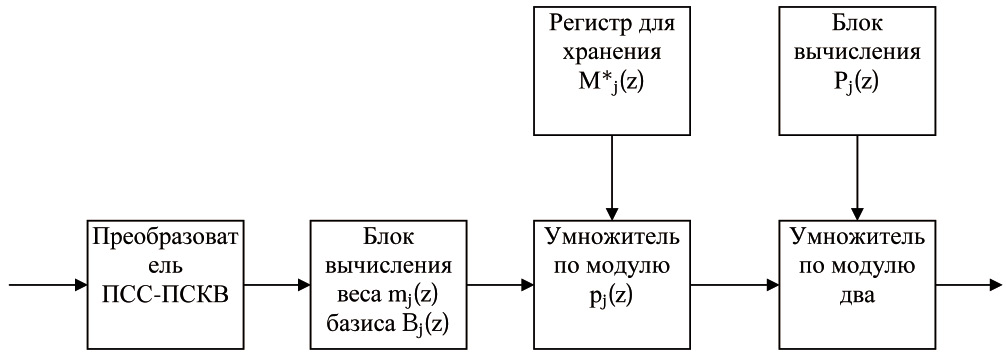
Рисунок 1 - Устройства вычисления ортогонального базиса для схемы разделения секрета, функционирующего в ПСКВ
Устройство работает следующим образом. На вход устройства подается значение модуля pi(z), где
. Данный полином поступает от другого пользователя, входящего в состав группы из t пользователей, желающих получить значение секретного ключа. Значение основания поступает на вход преобразователь из позиционной системы в полиномиальную систему класса вычетов. С выхода данного преобразователя ПСС-ПСКВ снимается значение pi(z)modpj(z). Полученный остаток поступает на вход блока вычисления веса mj(z) для ортогонального базиса Bj(z).
Затем вычисленное значение веса mj(z) ортогонального базиса Bj(z), как наглядно видно на рисунке 1, подается на первый вход умножителя по модулю pj(z), на второй вход которого поступает с регистра хранения значение затемненного секретаM*j(z). Полученный результат поступает на первый вход умножителя по модулю два. Данное устройство реализует вычисление
(16)
Пользователя группы обмениваются вычисленными значениями M*j(z)Bj(z), а затем, используя выражение (7), вычисляют зашумленный образ секретного ключа M*(z). После этого, зная значения полиномов r(z) и px(z), пользователи способны определить и сам секретный ключM(z).
Рассмотрим алгоритм работы блока вычисления веса ортогонального базиса.Структура этого блока показана на рисунке 2.
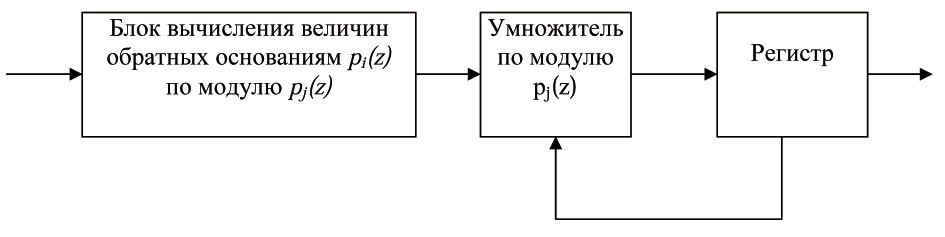
Рисунок 2 – Структура блока вычисления веса ортогонального базиса
Вычисленное значение pi(z)modpj(z) подается на вход блока вычисления величин обратных основаниям pi(z)по модулю pj(z).С выхода последнего снимается полученное значение mii(z)=pj(z)-1modpj(z). Это значение подается на первый вход умножителя по модулю pj(z). Второй вход этого умножителя подключен к выходу регистра. В данный регистр записываются промежуточные результаты вычисления выражения (15). Таким образом, за t тактов будет получено значение веса ортогонального базиса Bj(z).
Выводы
Таким образом, применение полиномиальной системы классов вычетов позволяет реализовать эффективную систему разделения секрета, позволяющей группе авторизованных пользователей восстанавливать общий секретный ключ по его образам. Применение разработанного алгоритма пересчета ортогональных базисов обеспечивает осуществление в реальном масштабе времени процесса восстановление секрета даже при динамически изменяющейся группе пользователей.