Количественная оценка инвестиционной привлекательности сложных экономических систем (СЭС) микро-, мезо- и макроуровня сегодня остается актуальной задачей в свете необходимости перераспределения финансового ресурса в наиболее эффективные направления деятельности СЭС. При количественной оценке эффективности, очевидно, оценивать нужно измеримое. Наиболее удобным в этой связи представляется использование понятия денежного потока затрат и выгод, которые обладают свойством стоимостной измеримости.
Содержательная постановка задачи и методы исследования
Определим инвестиционную привлекательность СЭС как разность инвестиционного потенциала и инвестиционного риска. Инвестиционный потенциал допускает свою численную оценку через такие показатели эффективности, как добавленная стоимость, чистая приведенная стоимость, прибыль и прочие показатели, позволяющие измерять абсолютные величины доходных и расходных составляющих при функционировании СЭС. Инвестиционный риск связан с возможностью возникновения угроз потребительской, коммерческой, финансовой, управленческой, информационной, экологической, социальной, политической природы, которые могут привести к кризисному развитию системы. В этой связи необходимо, чтобы инвестиционный риск допускал свое численное измерение, например, в суммах затрат на избежание, устранение риска либо в суммах потенциальных потерь. Такой подход позволит связать в единой модели производственный потенциал с инвестиционными рисками в СЭС и даст возможность повысить обоснованность оценки инвестиционной привлекательности.
При решении задачи оценки инвестиционной привлекательности региона необходимо учитывать интересы, как минимум, потребительского сектора (населения) и управляющих органов региона, несущих бремя возникающих для них рисков в виде социальных и экологических бедствий или лишения властных полномочий в результате провалов реализации различных направлений социальной, экологической или экономической политики. В этой связи решение указанной задачи затруднительно без использования методов математического моделирования и разработки автоматизированных средств анализа построенных моделей.
В данной работе предлагается многокритериальная математическая модель оценки инвестиционной привлекательности региона, рассматривающая как оценку экономической эффективности его производственного сектора, так и оценку возникающих при функционировании региональной социально-экономической системы рисков. При минимизации риска кризисного функционирования региональной системы, включающей такие подсистемы, как производственный, потребительский сектора и региональный управляющий центр, целесообразно использовать такой показатель, как определяемый экспертно уровень затрат (в материальном или стоимостном выражении) на устранение предполагаемого риска. Например, для управляющего центра это могут быть затраты на поддержку банковской системы, социальных программ, для производителя – вложения в очистные сооружения и т.д. В этой связи для оценки инвестиционной привлекательности региона необходимо построить многокритериальную оптимизационную линейную модель региона с критерием максимизации значения его целевой функции в виде линейной свертки выраженных в стоимостном виде критериев его подсистем минус значение соответствующего критерия минимизации суммы возникающих при этом рисков. Если для каждого k-го риска развития подсистемы заданы или найдены – экспертно или путем обработки статистических данных – линейные зависимости
rk=ak–bkxk
рисков rk от затрат xk на их избежание (исключение, уменьшение), то коэффициенты ak можно трактовать как максимальные издержки, которые может понести система в случае отсутствия затрат на k-ом рисковом направлении функционирования подсистемы, а коэффициенты bk – как весовые коэффициенты, отражающие относительную значимость k-го риска. Линейность указанной модели позволит применить к ней эффективные численные методы и автоматизированные программные средства инвестиционного анализа при практически значимых размерностях решаемой многокритериальной и многопараметрической задачи.
Математическая модель
В работе [3] построена трехкритериальная математическая модель региона, для которой, с использованием z-оператора, получена ее статическая версия. Указанная модель представляет собой задачу линейного программирования, допускающую эффективный численный анализ симплекс-методом. Рассмотрим ее модификацию, представляющую собой трехкритериальную модель взаимодействия регионального производственного, потребительского секторов и управляющего (налогового) центра с учетом рисков деятельности каждого из участников, которая, в предположении линейной зависимости рисков от затрат, принимает вид:
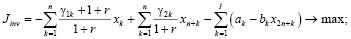
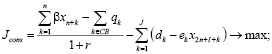
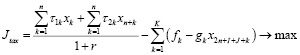 ;
;
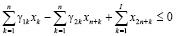 ;
;
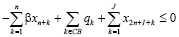 ;
;
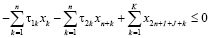 (1)
(1)
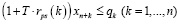 ,
,
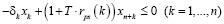 ,
,
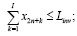
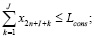
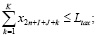
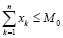 ,
,
где n – количество ОПФ; I, J, K – соответственно количество рисков для производственного, потребительского секторов и управляющего центра; xk – стоимость приобретаемых ОПФ k-го вида (инвестиции в основные фонды); xn+k – выручка от продажи продукции, произведенной на k-м ОПФ; x2n+i (i=1,…,I) – затраты на избежание (устранение) i–го риска производственного сектора; x2n+I+j (j=1,…,J)– затраты на избежание (устранение) j–го риска потребительского сектора; x2n+I+J+k (k=1,…,K) – затраты на избежание (устранение) k–го риска управляющего центра; сk – стоимость k-го ОПФ; Pk – стоимость продукции, произведенной на k-ом ОПФ; Vk – производительность k-го ОПФ; Tk – время полезного использования k-го ОПФ; T – горизонт планирования инвестиционного проекта; r – ставка дисконтирования на всем горизонте планирования; qk – спрос на продукцию, произведенную на k-ом ОПФ; СВ (consumer basket) – потребительская корзина; ak, dk, fk – максимальные издержки в случае отсутствия затрат на k-м рисковом направлении функционирования производственной, потребительской и управляющей подсистем соответственно; bk, ek, gk – весовые коэффициенты относительной значимости k-го направления функционирования производственной, потребительской и управляющей подсистем соответственно; 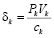 – максимальная фондоотдача k-го ОПФ производственной подсистемы; rps(k) – экспертно задаваемые коэффициенты, отражающие, во сколько раз выручка на стадии послепродажного сервиса больше выручки от продаж k-го вида продукции; αi, i=1,…,4 – соответственно ставки налогов на добавленную стоимость, на имущество и на прибыль, а также страховых взносов производственного сектора региона; p – средний процент оборотных затрат в регионе в сумме всех затрат регионального производственного сектора; β – средний процент выручки от продаж регионального производственного сектора, выделяемый на ФОТ; Linv, Lcons, Ltax – соответственно максимальные затраты на избежание (устранение) всех выделенных рисков производственного, потребительского секторов и управляющего центра;
– максимальная фондоотдача k-го ОПФ производственной подсистемы; rps(k) – экспертно задаваемые коэффициенты, отражающие, во сколько раз выручка на стадии послепродажного сервиса больше выручки от продаж k-го вида продукции; αi, i=1,…,4 – соответственно ставки налогов на добавленную стоимость, на имущество и на прибыль, а также страховых взносов производственного сектора региона; p – средний процент оборотных затрат в регионе в сумме всех затрат регионального производственного сектора; β – средний процент выручки от продаж регионального производственного сектора, выделяемый на ФОТ; Linv, Lcons, Ltax – соответственно максимальные затраты на избежание (устранение) всех выделенных рисков производственного, потребительского секторов и управляющего центра;
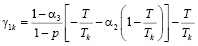 ,
,
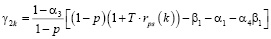 ,
,
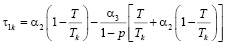 ,
,
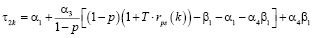 .
.
Модель (1) представляет собой многокритериальную задачу линейного программирования (ЗЛП) с размерностью матрицы модели (2n+7)×(2n+I+J+K). Целевые критерии Jinv, Jcons, Jtax в (1) содержательно представляют собой сальдо денежных потоков соответственно производственного и потребительского секторов и управляющего центра (налоговые сборы), приведенных по ставке дисконта r, учитывающей требования инвесторов по доходности проекта и инфляционную составляющую. Ограничения в (1) имеют следующий содержательный смысл соответственно: первое-третье – неотрицательность собственных средств (платежеспособность) регионального производственного и потребительского секторов и управляющего центра, четвертое – ограничение выпуска продукции технико-экономическими возможностями ОПФ с коэффициентом пропорциональности в виде их фондоотдачи, пятое – ограничение выпуска уровнем спроса на продукцию. Последняя группа неравенств отражает финансовые и инвестиционные ограничения.
Заключение
Предложенная математическая модель позволяет учитывать такие существенные для функционирования социально-экономической системы региона факторы, как соотношение производственных затрат (общих, оборотных, на оплату труда, амортизации), налоговый потенциал, ценообразование, спрос, влияние на эффективность проекта периода послепродажного обслуживания инновационной продукции и другие факторы. Задача (1), путем линейной свертки своих критериев, сводится к эквивалентной ей [4] однокритериальной ЗЛП, подверженной эффективному теоретическому и численному анализу [2]. Проведенные с помощью пакета [1] предварительные численные расчеты на модельных данных показали существование решения в предложенной модели.
Таким образом, в данной работе представлена математическая модель оценки инвестиционной привлекательности региональной СЭС как совокупности выраженной в едином стоимостном измерении оценки инвестиционного потенциала и инвестиционного риска.



