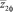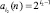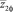Десятичная система счисления по плотности записи уступает многим другим системам счисления, но по удобству и в силу привычки по частоте пользования человеком на момент 02.07.2011 превосходит другие системы счисления (из Интернета).
Двоичная система счисления для ряда простых чисел должна стать эффективной позиционной системой. В ней используется всего две целые цифры: 0 и 1 [1].
Квантование простого числа. Любое простое число можно представить как квантованный в двоичной системе дискретный сигнал. При квантовании вся область значений сигнала разбивается на уровни, количество которых должно быть представлено в числах заданной разрядности [2]. Расстояние между этими уровнями называется шагом квантования, и он для не разреженного ряда простых чисел равен 1. Количество этих уровней (разрядов двоичной системы счисления) зависит от мощности квантуемого ряда простых чисел.
500 простых чисел. Примем ряд простых чисел a(n) = {2, 3, 5, ..., 3571} при n = {1, 2, 3, ..., 500} . В табл. 1 приведены фрагменты квантования на граничных переходах (реперах) между разрядами i2 двоичной системы счисления. Слева дан i10 десятичной системы.
Известно давно, что для чисел, растущих закономерно, например, для степеней двойки, было бы, конечно, нелепо разыскивать экземпляр, превосходящий все известные. Для простых же чисел прилагаются громадные усилия, чтобы именно это и сделать. Простые числа подвергались факторизации, т.е. разложению по множителям и числам с большими степенями двойки.
Вот эта увлечение и не позволило математикам применить двоичную систему для анализа не множителей любого простого числа, а квантованных в двоичной системе слагаемых.
Свойства простого числа. По иерархии рассмотрим несколько основных свойств.
1. Любое простое число содержит разряды i2 = 1, 2, ... двоичной системы и составляющие
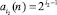 (1)
(1)
2. Любое простое число равно сумме составляющих с учетом матрицы инцидентности
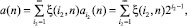 (2)
(2)
где ξ(i2, n) – матрица инцидентности, причем всегда ξ(i2, n) = 0 ∨ 1. Для бесконечномерного ряда простых чисел имеем уровни квантования или область разрядов двоичной системы i2 = (1, ∞).
Таблица 1
Ряд простых чисел в десятичной и двоичной системах счисленияПример вычислений по формуле (2) приведен в табл. 2.
| Мощность ряда | Разряд числа i10 | Порядок n простого числа | Простое число a(n) | Разряд числа i2 двоичной системы исчисления (уровень квантования) | |||||||||||
| 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | ||||
Значение части 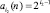 простого числа по уровню квантования простого числа по уровню квантования |
|||||||||||||||
| 2048 | 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||||
| 4 | 1 | 1 | 2 | 1 | 0 | ||||||||||
| 1 | 2 | 3 | 1 | 1 | |||||||||||
| 1 | 3 | 5 | 1 | 0 | 1 | ||||||||||
| 1 | 4 | 7 | 1 | 1 | 1 | ||||||||||
| 25 | 2 | 5 | 11 | 1 | 0 | 1 | 1 | ||||||||
| 2 | 6 | 13 | 1 | 1 | 0 | 1 | |||||||||
| 2 | 7 | 17 | 1 | 0 | 0 | 0 | 1 | ||||||||
| 2 | 8 | 19 | 1 | 0 | 0 | 1 | 1 | ||||||||
| 2 | 9 | 23 | 1 | 0 | 1 | 1 | 1 | ||||||||
| 2 | 10 | 29 | 1 | 1 | 1 | 0 | 1 | ||||||||
| 2 | 11 | 31 | 1 | 1 | 1 | 1 | 1 | ||||||||
| 2 | 12 | 37 | 1 | 0 | 0 | 1 | 0 | 1 | |||||||
| 2 | 13 | 41 | 1 | 0 | 1 | 0 | 0 | 1 | |||||||
| 2 | 14 | 43 | 1 | 0 | 1 | 0 | 1 | 1 | |||||||
| 2 | 15 | 47 | 1 | 0 | 1 | 1 | 1 | 1 | |||||||
| 2 | 16 | 53 | 1 | 1 | 0 | 1 | 0 | 1 | |||||||
| 2 | 17 | 59 | 1 | 1 | 1 | 0 | 1 | 1 | |||||||
| 2 | 18 | 61 | 1 | 1 | 1 | 1 | 0 | 1 | |||||||
| 2 | 19 | 67 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | ||||||
| 2 | 20 | 71 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | ||||||
| 168 | 3 | 30 | 113 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | |||||
| 3 | 31 | 127 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||
| 3 | 32 | 131 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |||||
| 3 | 33 | 137 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |||||
| 168 | 3 | 53 | 241 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | ||||
| 3 | 54 | 251 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | |||||
| 3 | 55 | 257 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||||
| 3 | 56 | 263 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | ||||
| 168 | 3 | 96 | 503 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | |||
| 3 | 97 | 509 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | ||||
| 3 | 98 | 521 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |||
| 3 | 99 | 523 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | |||
| 1229 | 4 | 171 | 1019 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | ||
| 4 | 172 | 1021 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | |||
| 4 | 173 | 1031 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | ||
| 4 | 174 | 1033 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | ||
| 1229 | 4 | 308 | 2029 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
| 4 | 309 | 2039 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | ||
| 4 | 310 | 2053 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | |
| 4 | 311 | 2063 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 1229 | 4 | 496 | 3541 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 4 | 497 | 3547 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | |
| 4 | 498 | 3557 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | |
| 4 | 499 | 3559 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | |
| 4 | 500 | 3571 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | |
В итоге получаем два типа нулей – тривиальные и нетривиальные. Первые расположены, как видно из данных двух таблиц, слева до вертикали 1 в каждом блоке. А нетривиальные нули располагаются внутри двух столбцов с 1, причем левый столбец 1 сдвигается по блокам по мере увеличения простого числа. В табл. 1 тривиальные нули показаны пустыми клетками.
Таблица 2
Ряд простых чисел (фрагмент) в десятичной системе счисления
|
Порядок n простого числа |
Простое число a(n) |
Разряд числа i2 двоичной системы исчисления |
|||||||||||
|
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
||
|
Значение части |
|||||||||||||
|
2048 |
1024 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
||
|
1 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
|
2 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
1 |
|
3 |
5 |
Тривиальные нули |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
0 |
1 |
||
|
4 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
2 |
1 |
|||
|
5 |
11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
8 |
0 |
2 |
1 |
|
6 |
13 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
8 |
4 |
0 |
1 |
|
7 |
17 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
16 |
0 |
0 |
0 |
1 |
|
8 |
19 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
16 |
0 |
0 |
2 |
1 |
|
9 |
23 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
16 |
0 |
4 |
2 |
1 |
|
10 |
29 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
16 |
8 |
4 |
0 |
1 |
|
11 |
31 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
16 |
8 |
4 |
2 |
1 |
|
12 |
37 |
0 |
0 |
0 |
0 |
0 |
0 |
32 |
0 |
0 |
4 |
0 |
1 |
Примечание. Начало (репер) каждого блока простых чисел показано жирным шрифтом.
3. Количество нетривиальных нулей стремится к бесконечности, так как ряд уровней квантования также стремится к бесконечности при условиях n → ∞, a(n) → ∞ и i2 = (1, ∞).
4. При первом разряде i2 = 1 двоичного числа (табл. 1) для условий n = 1 и a(n) = 2 инцидентность равна ξ(i2, n) = 0, а для ряда некритичных простых чисел P = {1, 5, 7, 11, 13, 17, ...} инцидентность равна ξ(i2, n) = 1, причем на всем протяжении n = (2, ∞) и a(n) = (3, ∞). Критичные простые числа требуют отдельного исследования.
5. Для некритичных простых чисел n = (2, ∞) и a(n) = (3, ∞) будут адекватными выводы, полученные на конечномерном ряду a(n) = {3, 5, ..., 3571} при мощности n = {1, 2, 3, ..., 500} .
Математический ландшафт. В замечательной серии фильмов «De Code» (19.07; 26.07 и 02.08.2011) ведущий Марк Дюсотой показывал графическую картину трехмерного «математического ландшафта» дзета-функции Римана. Все обращают внимание на нетривиальные нули на критической линии. Их уже насчитали несколько триллионов.
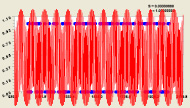
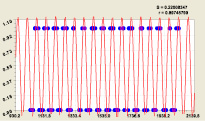
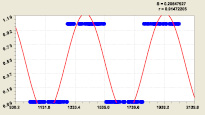
Но нас привлекло в этом в ландшафте другое – круто поднимающиеся склоны при приближении n → 0. Расклад в двоичной системе все бесконечно высокие «горы» превращает в выступы одинаковой высоты, равной единице. На рис. 1 приведен трехмерный график, для наглядности построенный только в части одного блока всего из 20 простых чисел.
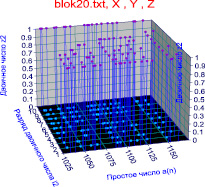
Рис. 1. Математический ландшафт фрагмента табл. 1 из 20 простых числе от 1031 до 1163
На рис. 1 появляется некий потолок из единиц, кроме «пола» из нетривиальных нулей. Между ними существует неизвестная связь. Тогда римановская сверхсложная поверхность, из-за представления в комплексных числах, преобразуется в двухслойный «пирог».
Придется рассматривать эти два слоя вдоль (по порядку простых чисел) и поперек (по разрядам i2). Для анализа введем показатель – двоичное число z2, принимающий вещественные значения.
Двоичное число вдоль ряда. Для анализа из данных табл. 1 были приняты только цельные блоки матрицы инцидентности, т.е. без тривиальных нулей. Для столбца с i2 = 1 придется исключить первую строку и тогда получим z2 = 1. Это и есть та «гора», от которой в поперечном направлении будут появляться нетривиальные нули. То, что условие z2 = 1 будет неизменным на всем бесконечномерном протяжении a(n) = (3, ∞), рассмотрим в другой статье.
Для a(n) = (2, 500) (кроме i2 = 1) получились среднестатистические значения (табл. 3).
Таблица 3
Влияние разряда
|
Разряд числа i2 |
Факт |
|
1 |
1 |
|
2 |
0,51000 |
|
3 |
0,50402 |
|
4 |
0,50605 |
|
5 |
0,48988 |
|
6 |
0,49284 |
|
7 |
0,51452 |
|
8 |
0,53518 |
|
9 |
0,54036 |
|
10 |
0,51117 |
|
11 |
0,60366 |
|
12 |
1 |
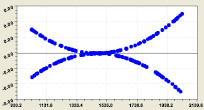
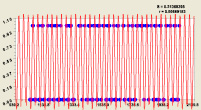
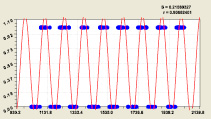
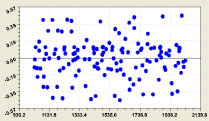
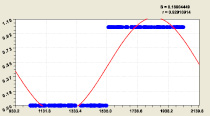
Влияние разряда i2. После идентификации устойчивыми законами [3, 4] для 500 строк (без i2 = 12) была получена (рис. 2) модель
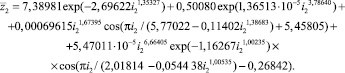 (3)
(3)
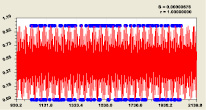
У четырехчленной модели распределения среднестатистического значения двоичного числа первая составляющая является законом экспоненциальной гибели (крутизна спада ландшафта), а вторая – законом экспоненциального роста, начиная от третьего разряда двоичной системы счисления. Затем дополнительные колебательные возмущения дают две волны адаптации. Первая из них имеет нарастающую амплитуду и показывает, что при условии i2 ≥ 3 половина амплитуды двоичного числа возрастает по закону показательного роста.
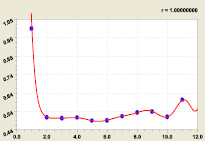
Рис. 2. График формулы (3): r – коэффициент корреляции
Вторая волна через какой-то разряд i2 будет приближаться к нулю. Картина совершенно изменится с дальнейшим ростом ряда простых чисел.
Максимальная относительная погрешность формулы (3) при i2 = 11 равна
100·2,47674e – 005/0,60366 = 0,0041 %.
При этом график очень схож с дзета-функцией Римана.
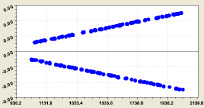
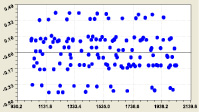
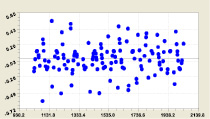
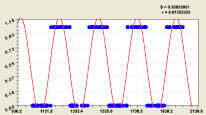
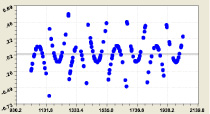
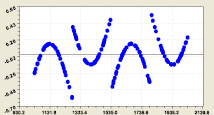
Блоки простых чисел. Вычислительные эксперименты показали, что мощность ряда нужно принимать исходя из полноты блоков матрицы инцидентности. Для примера берем блок № 11 с фрагментом, имеющим параметры: n = (173,309), a(n) = (1031,2039), i2 = (1,11). Сравнение показало существенность мощности ряда простых чисел, у которого порядковый номер имеет только вспомогательное значение. Показателем становится среднестатистическое (только не среднеарифметическое) двоичное число, а объясняющей переменной – само простое число.
Расчеты по блоку № 11 (рис. 3) приведены в табл. 4 и были выполнены по формуле
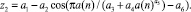 (4)
(4)
Таблица 4
Влияние простого числа на двоичное число по разрядам двоичной системы счисления
|
Разряд числа i2 |
Часть
|
Cредне-статистическое
|
Параметры статистической модели (4) двоичного числа |
Коэффициент корреляции r |
|||||
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
||||
|
1 |
1 |
1 |
0,5 |
-0,5 |
0 |
0 |
0 |
0 |
1 |
|
2 |
2 |
0,51825 |
0,5 |
0,5 |
2 |
0 |
0 |
1,59217 |
1 |
|
3 |
4 |
0,51825 |
0,5 |
0,70711 |
4 |
0 |
0 |
1,57080 |
1 |
|
4 |
8 |
0,53285 |
0,50079 |
0,64897 |
8,00054 |
0 |
0 |
-4,72553 |
0,9251 |
|
5 |
16 |
0,48175 |
0,50339 |
-0,64642 |
15,99613 |
0 |
0 |
4,82479 |
0,9069 |
|
6 |
32 |
0,40876 |
0,50997 |
0,63517 |
32,02910 |
0 |
0 |
1,46990 |
0,8975 |
|
7 |
64 |
0,51825 |
0,52117 |
0,63090 |
66,31876 |
-0,00066974 |
1 |
0,090540 |
0,9066 |
|
8 |
128 |
0,51095 |
0,50345 |
0,61806 |
129,7168 |
8,62532е-5 |
1,11225 |
0,94630 |
0,9132 |
|
9 |
256 |
0,48175 |
0,49203 |
0,64200 |
266,3384 |
1,85033е-5 |
1,52406 |
0,73950 |
0,9147 |
|
10 |
512 |
0,48905 |
0,50536 |
0,61721 |
682,0366 |
-0,34387 |
0,64381 |
-0,35596 |
0,9291 |
|
11 |
1024 |
1 |
0,5 |
-0,5 |
0 |
0 |
0 |
0 |
1 |
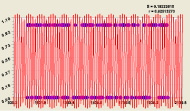
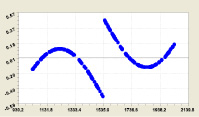
Если не учитывать первый и последний разряды двоичной системы, то наиболее близко к рациональному числу 1/2 по вещественным значениям формулы (4) находится разряд i2 = 2.
Как видно из графиков на рис. 3, остатки приближаются к нулю только при двух разрядах 2 и 3. В остальных случаях они находятся во всём промежутке (–0,5; +0,5).
Критические нули или единицы? Формула (4) по мере приближения ко второму разряду постепенно редуцируется до выражения
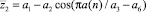 ,
,
получая постоянную частоту колебания с полупериодами 2 или 4. Критичными становятся как нули, так и единицы.
Вещественная часть 1/2. Из Интернета известно: «А вот знаменитая гипотеза Римана, что вещественная часть корня всегда в точности равна 1/2, ещё никем не доказана, хотя её доказательство имело бы для теории простых чисел в высшей степени важное значение».
Уравнение (4) дает, что не только вещественная часть корня равна 1/2. В формулах
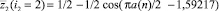
и
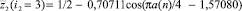 (5)
(5)
выражение перед функцией косинуса на критичной линии точно равно 1/2. Параметры 1,59217 и 1,57080, показывающие сдвиг волны с постоянной амплитудой, очень близки к иррациональному числу π/2, а число 0,70711 близок к π/4. Появление числа пространства π превращает уравнение (4) в модель пространственного сигнала. Он характеризуется симметричным вейвлетом с постоянной амплитудой ±1/2 и переменной частотой (в формуле – полупериодом).
Дзета-функции Римана имеет нули в отрицательных четных, кратных 2. Но данные табл. 3 показывают, что кратность появления нетривиальных нулей равна 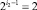 . Тогда по Риману получается
. Тогда по Риману получается 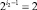 только при условии i2 = 2, то есть именно на критичной линии.
только при условии i2 = 2, то есть именно на критичной линии.
Заметим также, что в дзета-функции в комплексных переменных принята функция синуса, но косинус лучше для действительных чисел, так как позволяет не обращать внимания на знаки в выражении под тригонометрической функцией. Косинус работает в обоих квадрантах на ряде натуральных чисел (0, 1, 2, ..., ∞). Поэтому он будет удачным и в ряде простых чисел.
Алгоритм прогнозирования простого числа. Пока мы не уверены в возможности прогнозирования очередного члена в ряду простых чисел. Но, через их преобразование в двоичной системе счисления, становятся понятными границы между блоками. Правила перевода десятичных чисел в двоичные [1] вполне достаточны для объяснения «прыжков» в ряду простых чисел.
Асимптотические реперы. Мощностью ряда простых чисел вполне можно управлять. Для этого из табл. 2 выпишем выделенные жирным шрифтом значения NR (табл. 4).
|
|
|
|
При разряде i2 = 2 двоичной системы |
Остатки после модели двоичного числа |
|
|
|
|
При разряде i2 = 3 двоичной системы |
Остатки после модели двоичного числа |
|
|
|
|
При разряде i2 = 4 двоичной системы |
Остатки после модели двоичного числа |
|
|
|
|
При разряде i2 = 5 двоичной системы |
Остатки после модели двоичного числа |
|
|
|
|
При разряде i2 = 6 двоичной системы |
Остатки после модели двоичного числа |
|
|
|
|
При разряде i2 = 7 двоичной системы |
Остатки после модели двоичного числа |
|
|
|
|
При разряде i2 = 8 двоичной системы |
Остатки после модели двоичного числа |
|
|
|
|
При разряде i2 = 9 двоичной системы |
Остатки после модели двоичного числа |
|
|
|
|
При разряде i2 = 10 двоичной системы |
Остатки после модели двоичного числа |
Рис. 3. Графики статистической модели (4) двоичного числа: S – дисперсия; r – коэффициент корреляции
Таблица 4
Асимптотические реперы ряда простых чисел в количестве 500 шт.
|
a(n) |
2 |
5 |
11 |
17 |
37 |
67 |
131 |
257 |
521 |
1031 |
2053 |
|
NR |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
2048 |
Выводы
Для доказательства гипотезы Римана о том, что вещественная часть корня всегда в точности равна 1/2, выполнено преобразование простых чисел в двоичной системе счисления. Появились геометрия простых чисел и стали наглядными нетривиальные и нетривиальные нули, а также новые критерии и свойства.
1. Гашков С.Б. Системы счисления и их применение. – М.: МЦНМО, 2004. – 52 с.
2. Сигнал. . – URL: http://ru.wikipedia.org/wiki/ %D0 %A1 %D0 %B8 %D0 %B3 %D0 %BD %D0 %B0 %D0 %BB.
3. Мазуркин П.М. Биотехнический закон и примеры из техники и эконометрики // Успехи современного естествознания. – 2009. – № 9. – С. 97–102.
4. Мазуркин П.М. Биотехнический закон и содержательная адекватность модели // Успехи современного естествознания. – 2009. – № 9. – С. 115–120.
5. Цагер Д. Первые 50 миллионов простых чисел // Успехи математических наук. – 1984. – Т. 39. – № 6(240) . – С. 175–190.




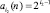 простого числа
простого числа