Знание взаимной растворимости воды и углеводородов необходимо для конструирования оборудования в очистительных и нефтехимических производствах. Углеводороды, наряду с другими примесями, должны быть удалены из воды. С другой стороны, содержание воды в углеводороде вместе с ухудшением качества продукта, его сертификата, может воздействовать на оборудование, вызывая коррозию. Поэтому для технологии очистительных процессов важны данные растворимости и улетучиваемости при различных термобарических условиях. Кроме того, в недрах Земли газовые и нефтяные залежи находятся в непосредственном контакте с водой при высоких параметрах состояния. Растворимость их в воде, фазовое равновесие в таких системах имеют большое значение для технологии добычи газа и нефти. Существующие теоретические модели [10, 11, 15, 24] правильно предсказывают общие закономерности в фазовом поведении таких сложных систем, но они далеки от количественной интерпретации даже для бинарных систем углеводород - вода. Нефть и газ различных месторождений по составу отличаются друг от друга, соответственно, отличается их фазовое поведение. В связи с этим целесообразно исследовать бинарные системы углеводородов и воды, а затем на их основе, используя различные закономерности, рассчитать свойства смесей нефти и воды при параметрах состояния соответствующих пластовым условиям.
В данной работе приведены результаты исследования фазовых равновесий бинарных несмешивающихся при нормальных условиях систем (гексан - вода, пентан - вода) на основе измерения PVTx - свойств в температурном интервале 300 - 680 К, давлениях до 60 МПа и в широком интервале плотностей на пьезометре постоянного объема [6].
Для подготовки смеси были использованы деаэрированная вода двойной дистилляции, н.гексан и н. пентан чистотой 99,94 и 99,91 % соответственно.
Измерения PVTx-свойств охватывают широкую область параметров состояния, включая области равновесий жидкость-жидкость (ж-ж) и жидкость-пар (ж-п). Термические свойства системы гексан-вода получены для девяти значений концентрации воды (в мольных долях) от 0,166 до 0,964 и системы пентан-вода получены для девяти значений концентрации воды от 0,110 до 0,925. Для каждой концентрации измерения проведены по десяти-одиннадцати изохорам, охватывающие широкий интервал паровых и жидкостных изохор. На рис. 1 представлена Р-Т диаграмма системы н.пентан-вода с концентрацией 0,209. На Р-Т диаграмме вдоль изохор наблюдаются изломы, соответствующие фазовым переходам ж-ж и ж-п. Соединение точек излома дает линии фазового равновесия, отделяющие трехфазную область от двухфазной и двухфазную область от однофазной. Изохора без излома проходит через точку максимума температуры - крикондентерму линии фазового равновесия. Отметим, что точка крикондертермы не всегда соответствует критической температуре. Общая картина всех Р-Т диаграмм имеет аналогичный вид. Линии фазовых переходов ж-ж и ж-п и их критические параметры по мере увеличения содержания воды в смеси приближаются друг другу. При концентрации, равной 0,257 для системы гексан-вода и 0,209 для системы пентан-вода, линии фазового равновесия ж-ж и ж-п имеют общую точку касания, и критические параметры их совпадают. Эта точка называется верхней конечной критической точкой (ВККТ) и является точкой азеотропа, так как в этой точке сосуществуют все три фазы: углеводородная жидкость, водная жидкость и пар. Критические параметры этой точки для системы пентан-вода имеют значения Тк = 463,8 К и Рк = 4,57 МПа, а для системы гексан-вода - Тк = 495,3 К и Рк = 5,28 МПа, которые хорошо согласуются с литературными данными [16‒18, 21, 22, 25]. При добавлении в систему воды растет общее давление, увеличивается содержание воды в газовой фазе и часть воды растворяется в углеводороде. Давление в системе увеличивается до начала образования второй жидкой фазы, и система переходит из двухфазного в трехфазное. Область равновесия между углеводородной жидкостью и газовой фазой ограничивается кривой трехфазного равновесия, линией нижнего локуса критических точек и кривой упругости пара чистого углеводорода. Температура трехфазного равновесия ниже температуры кипения чистых компонентов при давлениях, равных давлению трехфазного равновесия. На Р-Т диаграмме область трехфазного равновесия является кривой, идущей от ВККТ в сторону более низкой температуры и давления. Углеводородная и водная жидкости находятся в равновесии при температурах ниже температуры ВККТ. С увеличением температуры увеличивается растворимость воды в жидком углеводороде и повышается нижняя граница давлений существования равновесия между жидкими фазами. При ВККТ растворимость воды в углеводороде наибольшая, и температура ВККТ является самой высокой температурой, при которой существуют все три фазы. Над нею исчезает жидкая фаза, богатая углеводородом.
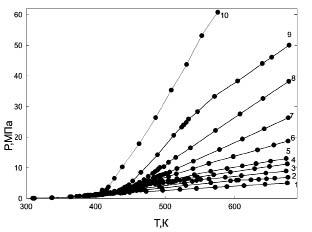
Рис. 1. Р-Т диаграмма системы н-пентан + вода с концентрацией
0.209 м.д. воды для различных изохор:
1 - ρ = 64.1; 2 - ρ = 96.1; 3 - ρ = 128.1; 4 - ρ = 160.2; 5 - ρ = 192.2; 6 - ρ = 256.3; 7 - ρ = 320.4;
8 - ρ = 384.2; 9 - ρ = 448.5; 10 - ρ = 512.6 (кг/см3)
Выше концентрации, соответствующей ВККТ, зависимость Р(Т) является гладкой и монотонной, без каких либо особенностей. Для этих концентраций на фазовых диаграммах критические условия не реализуются. Снова критические точки появляются для концентраций выше 0,882 м.д. На изоплетах проявляются локальный температурный максимум и локальный температурный минимум. С увеличением концентрации разность между экстремумами увеличивается. В области высокого давления все изоплеты показывают крутой подъем. На верхнем локусе критических точек обнаружен температурный минимум, соответствующий концентрациям 0,935 и 0,925 м.д. соответственно для обоих смесей.
Согласно классификации Кониненбурга и Скотта [23] фазовая диаграмма бинарных систем углеводород - вода относится к III типу. Нижний локус линии критических точек (рис. 2) начинается в критической точке чистого углеводорода и заканчивается в ВККТ. Верхний локус начинается в критической точке воды и, проходя через температурный минимум, направляется в область высоких давлений. Точка, соответствующая минимуму температуры, разделяет двухфазную область на две части. Правая часть соответствует равновесию ж-п и при повышении температуры смыкается с критической точкой воды, а левая часть двухфазной области соответствует равновесию газ-газ второго типа и продолжается выше критической температуры воды. Точка, где смыкаются кривые газ-газ и ж.-п., называется двойной критической точкой (ДКТ). На Р-Т диаграмме область фазового равновесия газ-газ ограничена кривой, идущей от ДКТ в сторону более высоких Т и Р, и изотермой, идущей от ДКТ в сторону более высоких давлений. С увеличением числа атомов углерода в углеводороде критическая кривая сдвинута к низким давлениям и к высоким значениям концентрации воды. Для ДКТ систем пентан + вода и гексан + вода получены параметры Тс = 625,5 К, Рс = 33,7 МПа и Тс = 627,7 К, Рс = 30,9 МПа соответственно. Явление ограниченной растворимости газов было обнаружено И.Р. Киричевским и сотрудниками еще в 1941 году и подробно исследовано Д.С. Циклисом [9]. Поведение систем вблизи ДКТ заметно отличается от их поведения вблизи обычных точек на линиях фазового равновесия. Общие свойства и анализ поведения систем с ДКТ приводятся в работах [4, 7], в которых авторы пришли к выводу, что с приближением к ДКТ для описания явления больше подходит теория фазовых переходов Ландау.
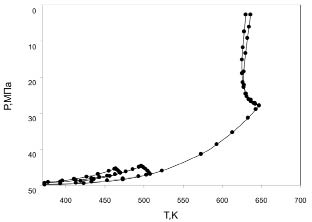
Рис. 2. Р-Т фазовые диаграммы, нижние и верхние критические линии
смесей вода-пентан и вода-гексан
Для аппроксимации кривой фазового равновесия жидкость-жидкость было использовано выраже-
ние [2, 12]
![]() (1)
(1)
где β, Δ, α - критические индексы, причем Δ и α фиксированы [5] (Δ = 0,50, α = 0,11); В0, В1, В2, В3 - критические амплитуды; t ≡ (Tc - T)/Tc - приведенная температура; ρc и Тс - соответственно критическая плотность и температура; знаки (+) и (-) относятся к правой и левой ветвям кривой сосуществования жидкость-жидкость.
Результаты расчетов показывают, что для фазового перехода жидкость-жидкость значения критического показателя b близки (в пределах погрешности расчетов) к 0,325. Это говорит о справедливости вывода о том, что жидкости вблизи точки фазового перехода жидкость-жидкость относятся к классу универсальности трехмерных изинговских систем.
Описание кривой сосуществования жидкость-пар производили согласно уравнению [2, 13]
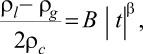 (2)
(2)
где ρl и ρg - плотности жидкой и паровой фаз соответственно; В - критическая амплитуда.
Результаты расчетов для бинарной смеси гексан - вода и пентан-вода показывают, что значение критического показателя b близко к 0.325, что характерно для трехмерных изинговских систем. Однако для концентраций, соответствующих ДКТ, величина b в два раза больше, что соответствует предположению [11] об удвоении критических индексов в двойной критической точке.
Термодинамические свойства бинарной системы гексан - вода вблизи критической линии жидкость-пар описывали с помощью кроссоверного уравнения состояния [3,19]. Его основная идея заключается в получении кроссоверных функций, переводящих шестичленное разложение Ландау в разложение Вегнера для свободной энергии Гельмгольца жидкости в околокритической области.
Удельную энергию Гельмгольца A(τ, ρ, ζ) записывают в виде [19]
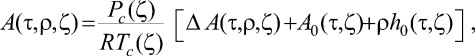 (3)
(3)
где ζ - полевая переменная, соответствующая концентрации х; R - молярная газовая постоянная; Рс - критическое давление; τ = [T - Tc(ζ)]/T; ΔA(τ, ρ, ζ) - сингулярная часть свободной энергии Гельмгольца; h0(τ, ζ) и A0(τ, ζ) - регулярные функции, которые представляются усеченными рядами Тейлора. ΔA(τ, ρ, ζ) зависит от так называемой кроссоверной функции Y, в зависимости от значения которой сингулярная часть свободной энергии Гельмгольца переходит в разложение Вегнера (в близкой окрестности критической точки) или в классический ряд Ландау (вдали от критической точки). Чтобы идентифицировать зависимости критических параметров от переменной ζ как зависимости от х накладывается условие равенства х = ζ на критической линии. Асимметрия реальной жидкости учитывается при переходе от модельных переменных к физическим переменным. Неуниверсальные константы вещества, характеризующие индивидуальные свойства системы, вычисляли на основе литературных данных и собственных PVTx экспериментальных исследований [5]. Необходимые при расчете зависимости критических параметров от концентрации аппроксимировали полиномами и сплайнами.
Кроссоверное уравнение состояния позволяет описывать давление бинарных смесей гексан - вода и пентан‒вода с погрешностью, не превышающей 3 %, в интервале изменения плотностей 0,50ρc ≤ ρ ≤ 1,7ρc (при T = Tc) и температур 0,95Tc ≤ T ≤ 1,7Tc (при ρ = ρc).
Список литературы
- Абдулагатов И.М., Базаев А.Р., Рамазанова А.Э. // ТВТ. - 1992. - Т.30, №6. - С. 897.
- Анисимов М.А. Критические явления в жидкостях и жидких кристаллах. - М.: Наука, 1987. - 272 с.
- Киселев С.Б., Поводырев А.А. // Теплофизика высоких температур. - 1996. - Т. 34, № 4. - С. 626-646.
- Кривохижа С.В., Луговая О.А., Фабелинский И.Л. // ЖЭТФ. - 1993. - Т. 103, Вып. 1. - С. 115.
- Расулов С.М., Расулов А.Р. // Теплофизика высоких температур. - 2000. - Т. 38, № 3. - С. 412-417.
- Расулов С.М., Хамидов М.М. // ПТЭ. - 1999. - С. 148.
- Собянин А.А. // УФН. - 1986. - Т.149, Вып. 2. - С. 325.
- Уолкер Дж.С., Вос Ч.А // В мире науки. - 1987. - №7. - С. 50.
- Циклис Д.С. Расслаивание газовых смесей. - М.: Химия. 1969. - 160 с.
- Abdulkadirova Kh. S., Khokhlachov S.P. // Fluid Phase Equil. - 1997. - Vol. 140. - P. 73.
- Anisimov M.A., Gorodetskii E.E., Kulikov V.D., Sengers J.V. // Phys. Rev. E. - 1995. - Vol. 51, №2. - P. 1199-1215.
- Aizpiri A.G., Correa J.A., Pena M.D. // J. Chem. Phys. - 1988. - Vol. 88, №3. - P. 1934-1943.
- Aizpiri A.G., Correa J.A., Rubio R.G., Pena M.D. // Phys.Rev.B. - 1990. - Vol. 41, №13. - P. 9003-9012.
- Brunner E. // J.Chem. Thermodyn. - 1990. - Vol. 22. - P. 335.
- Christoforakos M., Franck E.U. // Ber. Bunsenges. Phys.Chem. - 1986. - Vol. 90. - P. 780.
- Connoly J.F. // J. Chem. and Eng. Data. - 1966. - Vol. 11, №1. - P. 13.
- De Loos Th.W., Penders W.G., Lichtenthaler R.N. // J. Chem. Thermodyn. - 1982. Vol. 14. - P. 83.
- De Loos Th.W., van Dorp J.H., Lichtenthaler R.N. // Fluid Phase Equil. - 1983. - Vol. 10. - P. 279.
- Jin G.X., Tang S., Sengers J.V. // Phys.Rev.E. - 1993. - Vol. 47, № 1. - P. 388-402.
- Kamilov I.K., Stepanov G.V., Malysheva L.V. et. al. // HighTemp.- High Press. - 1997. - Vol. 29. - P.237.
- Roof J.G // J. Chtm. and Eng. Data. - 1970. - Vol.15, №2. - P. 301.
- Tsonopoulos C., Wilson G.M. // AIChE Journal. - 1983. - Vol. 29, №6. - P. 990.
- Van Konynenburg P.H., Scott R.L. // Phil. Trans. Rou. London. - 1980. - Vol. 298, №A1442. - P. 495.
- Victorov A.I., Frederslund A.A., Smirnova N.A. // Fluid Phase Equil. - 1991. - Vol. 66. - P. 187.
- Yiling T., Michelberger Th., Franck E.U. // J. Chem. Thermodyn. - 1991. - Vol. 23. - P. 105.



