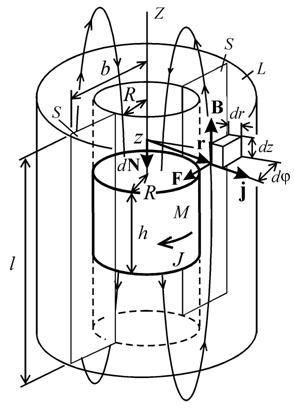
Рис. 1. Схема расчета
Пусть электропроводящая жидкость L, в которой течет радиальный постоянный электрический ток плотности j, находится между двумя цилиндрическими электродами с радиусами R и b (рис. 1). Если I - сила тока, то его плотность на расстоянии r от оси симметрии Z:
![]() , (1)
, (1)
где l - высота электродов. Внутри электрода с меньшим радиусом находится цилиндрический магнит M высотой h, расположенный симметрично по отношению к электродам и к электропроводящей жидкости. Отличительной особенностью такой схемы является отсутствие так называемых боковых токов [3], являющихся мешающим фактором в изучении электромагнитного вращения.
На элемент объема жидкости dV=dzrdjdr, находящийся в магнитном поле индукции B, действует магнитная сила
![]() . (2)
. (2)
Нас будет интересовать Z-компонента вращательного момента (момента сил)
![]() , (3)
, (3)
поэтому имеет смысл рассматривать только Z-компоненту индукции магнитного поля, создаваемого намагниченным цилиндром:
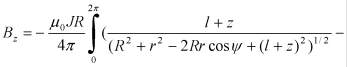
![]() , (4)
, (4)
где J - намагниченность. Поскольку
![]() , (5)
, (5)
то интегрирование по углу j в пределах от 0 до 2p и по z в пределах -(h+l)/2<z<(l-h)/2 дает
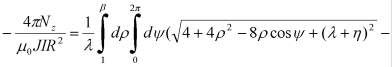
![]() , (6)
, (6)
где ρ=r/R, η=h/R, λ=l/R, β=b/R.
Предполагается, что весь вращательный момент передается плоскостям (парусам) S, жестко соединенным с намагниченным телом. Это единственный "технический" аспект настоящей работы. В остальном же, все это имеет отношение к основным законам физики взаимодействия токов и намагниченных тел. Получается, что электропроводящая жидкость в магнитном поле заставляет вращаться источник этого поля. Ни к каким нарушениям законов сохранения импульса, момента импульса и, тем более, сохранения энергии это не приводит [2]. Третий же закон Ньютона в незамкнутой системе выполняться не обязан [4].
Обратим внимание, при β>>1 интеграл (6) зависит только от двух величин: приведенной высоты магнита h и приведенной толщины слоя λ. Поэтому результаты численного интегрирования, представленные на рис. 2, носят достаточно универсальный характер. Самое интересное заключается в том, что при заданной величине силы тока I момент сил самодействия максимален при минимально возможной толщине слоя электропроводящей жидкости. При этом максимум вращательного момента
![]() (7)
(7)
имеет место при пятикратном превышении высоты магнита над его радиусом. Имеет смысл вычислить момент сил самодействия для параметров λ=η и η=1.6, частично соответствующих экспериментальным результатам [2]. Оказалось, что в этом случае Nz≈3.6μ0JIR2/4π, что при силе тока I=5А намагниченности J=2×105А/м и радиусе магнита R=0.065м составляет величину 3.8×10-4Н×м. При этом отличие этого значения от экспериментального результата 2×10-4Н×м [2] может быть объяснено неполной передачей вращательного момента электропроводящей жидкостью намагниченному телу. Несмотря на кажущуюся простоту работы, основной результат работы оказался достаточно оригинальным. Существование самодействия удалось подтвердить не только качественно, но и количественно. Поэтому всякие догматические заключения о нереальности этого явления [5] в дальнейшем едва ли следует воспринимать серьезно.
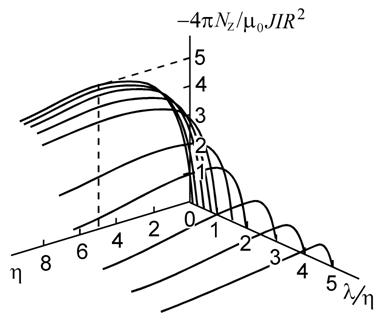
Рис. 2. Момент сил самодействия как функция приведенной высоты магнита h и приведенной толщины слоя электропроводящей жидкости λl при b→∞.
СПИСОК ЛИТЕРАТУРЫ:
- Герасимов С.А., Сташенко В.В. Парусный эффект в электромагнитном вращении. // Учебная физика. 2004. № 6. С. 29-37.
- Герасимов С.А., Прядченко В.В. Инверсный парусный эффект в магнитогидродинамике. // Вопросы прикладной физики. 2006. № 13. С. 72-73.
- Сигалов Р.Г., Шаповалова Т.И., Каримов Х.Х., Самсонов Н.И. Магнитные поля и их новые применения. - М.: Наука. 1976. - 104c.
- Герасимов С.А. Самодействие как оно есть. // Инженер. 2006. № 4. С. 12-14.
- Graneau N. The Finite Size of the Metallic Current Element. // Physics Letters A. 1990. V. 147. No 2-3. P. 92-96.



