На сайте «Научный Форум dxdy» в Интернете [1] есть рубрика «Феномен Великой теоремы Ферма», в которой могут высказаться все желающие, заинтересовавшиеся проблемой доказательства Великой теоремы (в дальнейшем будем пользоваться аббревиатурой ВТФ) и озадаченные полным отсутствием общественной реакции высоких математических кругов на состояние этой проблемы в настоящее время. Поскольку интерес к проблеме стал поистине всенародным (по крайней мере, среди творческой интеллигенции, знакомой в той или иной степени с математикой; см. огромное количество сообщений в Интернете на эту тему), следует, наверное, подробнее рассказать о последних событиях в исследовании теоремы Ферма. Эта информация будет особенно важна для педагогов, преподающих математику в средней и высшей школе.
Прежде всего, отметим, что ошибочное доказательство А.Уайлса (см. [2]), с помощью которого официальная математика решила навсегда закрыть проблему ВТФ для общественного сознания [3-4], до сих пор является образцом глубокомыслия и недосягаемости для понимания в точных науках на Западе и не вызывает там никаких вопросов или угрызений совести относительно опасной (если не сказать больше) деятельности своих ученых. Однако российский Левша не даст себя обмануть, хотя высокое научное руководство, заигрывающее с западными авторитетами, и пытается зарыть его таланты в землю [5].
К сожалению, в современной фундаментальной науке произошла селекция бездарных и недалеких ученых, научившихся только защищать диссертации в своем «узком кругу» и приобретать пожизненное право принадлежать к элите общества (см., например, [6]). В такой среде даже талантливые ученые не в силах противостоять корпоративному мнению безликой массы. В России подобная селекция возникла не на пустом месте и имеет глубокие исторические корни, обусловленные национальными особенностями российского менталитета (см. сочинения А.С. Грибоедова, М.Е. Салтыкова-Щедрина, М.А. Булгакова и других российских писателей). Как известно, форпостом российской науки является Российская Академия наук, традиционно (хотя, может быть, и неформально) контролирующая все основные направления научной и образовательной деятельности в стране (ВАК, научные журналы и фонды, молодежную научно-популярную прессу и другие научно-образовательные издания и учреждения). Поэтому пробиться независимой мысли сквозь частокол верноподданнических научных и околонаучных организаций практически невозможно.
Но не следует слишком огорчаться по поводу того, что вас не поняли, скажем, академики с РАН. Гораздо важнее, если у исследователей будет возможность обсуждать свои работы с теми, кто помоложе, и с учеными и преподавателями, не лишенными творческой жилки. Только так могут быть преодолены трагические ошибки прошлого. Например, именно благодаря подобной возможности и независимой экспертизе, мир узнал об открытиях Эвариста Галуа, раздавленного Французской Академией наук в самом начале его творческой деятельности [7].
2. Какой урок можно извлечь из ошибочного доказательства Уайлса?
Итак, обратимся сначала к работе А.Уайлса для того, чтобы понять основную идею его доказательства (более подробно об этом см. [2,8]). Эта идея состоит в следующем: если рассматривать гипотетическое уравнение Ферма в целых числах как уравнение для проективной прямой, пересекающей проективную эллиптическую кривую в трех рациональных точках, то такая кривая, называемая кривой Фрея, не была бы модулярной; но Уайлс показал, что все эллиптические кривые рассматриваемого вида модулярны; отсюда следовал вывод о том, что решений уравнения Ферма в целых числах не существует.
Основная трудность реализации данной схемы доказательства заключается в изучении возможности построения кривой Фрея, которое так и не было осуществлено: Г.Фрей просто вписал гипотетическое решение уравнения Ферма в свою «эллиптическую» кривую, а А.Уайлс принял ее на веру, не позаботившись о том, чтобы математически корректно провести такое построение. Насколько это сложная и нетривиальная задача теории эллиптических кривых, можно судить, например, по работе [9], ориентированной на любознательных школьников старших классов. Самые сильные математики в мире пытались решить эту задачу, но до сих пор так и не смогли этого сделать, еще раз подтвердив народную мудрость: трудно искать черную кошку в темной комнате, особенно, когда ее там нет.
К счастью, для исследователей, не владеющих аппаратом теории групп и абелевых многообразий, есть способ провести независимое расследование построения кривой Фрея на евклидовой плоскости и придти к поразительным результатам, затрагивающим самые основы математической науки. Для этого настоятельно рекомендуем прочитать лекцию Х.Крафта [9] о поиске рациональных точек на алгебраических кривых n-ого порядка (при целом
n > 2). В частности, в этой лекции имеется элементарное доказательство следующего утверждения: если имеются две рациональные точки кривой 3-его порядка на евклидовой плоскости и прямая, проходящая через эти точки, пересекает данную кривую еще в одной точке, то эта точка также является рациональной.
При обобщении этого утверждения для абелевых многообразий, простейшим примером которых являются проективные эллиптические кривые, также действует аналогичный закон группового сложения: сумма трех точек на проективной кривой равна нулю тогда и только тогда, когда они лежат на одной прямой. При этом надо помнить, что когда говорят в арифметике эллиптических кривых о «сложении точек», то подразумевают групповую операцию объединения элементов группы, а не сложение геометрических точек, что само по себе абсурдно.
Применим теперь правило трех точек для построения кривой Фрея на евклидовой плоскости. Опять-таки воспользуемся работой [9] для того, чтобы преобразовать кривые Ферма (см. также [8,10]) в прямую заменой переменных: xn = X, yn = Y, zn = Z. Действительно, уравнение Ферма, записанное для целых чисел x, y, z при n≥ 3:
zn = xn + yn (1)
преобразуется в уравнение: Y = - X + Z, в котором переменные X и Y характеризуют прямую, пересекающую оси X и Y декартовой системы координат под углом 45о. На этой прямой условно можно отметить точки, соответствующие гипотетическому целому решению уравнения Ферма (1): Bn = -An + Cn, где А, В, С - целые числа. При повороте полученной прямой до совмещения ее с осью Х длины отрезков между точками прямой на евклидовой плоскости сохраняются. Границы отмеченных отрезков соответствуют правилу трех точек, известному из арифметики эллиптических кривых, т.е. из четырех точек равенства: An + Bn - Cn = 0 мы можем выбрать три независимых элемента для того, чтобы построить алгебраическую кривую 3-ей степени [2]:
Y2 = X (X + An)(X - Bn) (2)
Таким образом, мы получили кривую Фрея, пересекающую ось Х в трех точках:
(Х = 0, Y = 0), (X = - An, Y = 0), (X = Bn, Y = 0)
(см. также [2]). Однако, является ли она эллиптической, как было заявлено Г.Фреем и А.Уайлсом при попытке доказать ВТФ методом от противного ? Очевидно, что нет, если учитывать нелинейность координат Х и Y при обратной замене переменных. Другими словами, уравнение (2) описывает иллюзорную геометрическую фигуру, похожую на обычную эллиптическую, определяемую формулой: y2 = x(x + u)(x - v) с линейными координатами x и y, где u, v - какие-либо рациональные числа, но на самом деле ею не являющуюся.
Противоречивый и неоднозначный характер кривой Фрея (2) не позволяет отнести ее к классу эллиптических кривых и поэтому ее сравнение по критерию модулярности с обычными эллиптическими кривыми неправомерно [2,8].
Вернемся в исходную точку доказательства А.Уайлса, чтобы еще раз пройтись по его логическим ступенькам и глубже осмыслить его центральную идею, почему-то тщательно законспирированную. Она заключается в представлении гипотетического уравнения Ферма (1) в виде группового сложения целых чисел (см. [2]): zn + xn + yn = 0, где zn, xn, yn - элементы конечной аддитивной группы 3-его порядка, имеющей обратные элементы (-zn), (-xn), (-yn). Эту группу можно изоморфно отобразить на диаграмме:
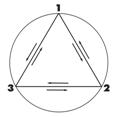
где цифры 1,2,3 соответствуют элементам группы, а стрелки между ними указывают на симметричные повороты в кольце преобразований (цифра 0 соответствует тождественному преобразованию). Основание группы равно 4 (по количеству имеющихся цифр 0,1,2,3). Далее предполагается, что рассматриваемая группа реализуется на точках (элементах) проективной эллиптической кривой, что собственно и является главным промахом в рассуждениях Г.Фрея и А.Уайлса, так как это второе предположение (после первого, когда уравнение Ферма записывалось в целых числах) не было обосновано, т.е. не было доказано, что элементами группы уравнения (1) являются отрезки прямых («точки на эллиптической кривой»), а не какие-либо другие, вообще говоря, нелинейные элементы.
Зададимся теперь вопросом, почему столь очевидная ошибка не была замечена профессионалами за многие годы самых восторженных отзывов в СМИ, обслуживающих официальную науку. Если отвлечься от чисто психологических моментов феномена ВТФ, которые играют в нем далеко не последнюю роль (см., например, [3-4]), то следует, по-видимому, обратиться к основаниям математических наук и постараться обнаружить в них источник поразительной слепоты профессиональных математиков. С этой целью обратим свое внимание на структуру уравнения (1), которая в работе [4] определена как бином Ферма. Бином Ферма (правая часть уравнения (1)) и бином Ньютона, записанные в положительных целых числах, не сводимы друг к другу при натуральном показателе степени n >1, что легко можно видеть из разложения бинома Ньютона в ряд:
(x + y)n = xn + ( x, y ) + yn,
где Δ( x, y ) - сумма всех промежуточных членов ряда, причем Δ( x, y ) = 0 только в том случае, если xy = 0, т.е. с исчезновением самого бинома Ньютона. Поскольку бином Ньютона обладает линейной структурой, т.е. может быть представлен полиномом n-ой степени от одного переменного, то, по-видимому, структура бинома Ферма в отличие от бинома Ньютона нелинейна и не может быть представлена на одной линейной числовой оси, требуя для своего адекватного представления расширения числового пространства. Поэтому попытки построить уравнение Ферма (1), пользуясь только возможностями одной стандартной числовой оси, обречены на провал и нужно искать другие геометрические представления натурального ряда чисел, могущие стать основой не только для построения нелинейной действительной оси, но и других числовых пространств, еще, может быть, не известных современной науке.
Пионером такого изначального и абсолютно независимого от ученого мнения других людей подхода в изучении чисел был, конечно, великий Ферма. В своих исследованиях он полагался, прежде всего, на естественные закономерности окружающего мира, а не на общепринятые соглашения каких-либо специалистов в той или иной области. Ограничиваясь затронутой здесь темой, можно сказать, что Ферма первым почувствовал глубокую потенциальную силу «геометрического места точек» числового пространства, от которого в дальнейшем ученые отказались при конструировании аналитических разделов математики. Такой мощный прорыв его гения в неизведанную область оказался для него самого загадочным, не позволив его холодному рассудку в полной мере осознать свое открытие и применить найденный геометрический метод в его других исследованиях по теории чисел.
3. Схема нативного доказательства ВТФ для n = 3 и всех других целых n > 3.
Итак, обратимся к нативному доказательству ВТФ, впервые представленному в [11] и предположительно найденному его первооткрывателем - Пьером де Ферма. Это доказательство было названо нами нативным по той причине, что намеренно придумать его было бы невозможно. Для этого надо потягаться разумом с Природой, что заведомо не равноценно, ибо все основополагающие знания человечества получены именно из Природы, как, например, теорема Пифагора в ее визуально очевидной геометрической трактовке. Поэтому и Ферма, когда исследовал пифагоровы тройки целых чисел, отыскал такую геометрическую фигуру, на которой могли бы быть изображены все прямоугольные треугольники с потенциально целочисленными катетами и целочисленными гипотенузами. Такая фигура была найдена (см. [11]) и была названа нами «фермаскопом» по причине самогенерирующейся цепочки рассуждений и построений, приведших Ферма к окончательной формулировке его Великой теоремы. Основным рабочим инструментом (если можно так выразиться) «фермаскопа», представленного на рис.1, явилась геометрическая теорема Евклида о средних пропорциональных, образующих две бесконечные геометрические прогрессии с натуральным индексом (при n 3):
![]()
![]() (3)
(3)
где z - радиус ОА большого круга «фермаскопа» на рис.1, x0 - изменяемый отрезок ОВ, y0 - соответствующий катет АВ прямоугольного треугольника ОАВ, k = ОС, l = СА, kn-3, kn-2, l n-3, ln-2 - средние геометрические в бесконечных цепочках уравнений (3), способ построения которых в виде сторон подобных прямоугольных треугольников показан на рис. 1.
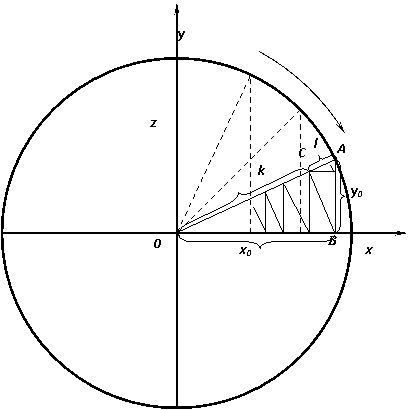
Рис. 1
Из (3) можно получить универсальное равенство в действительных числах, демонстрирующее, что любые одинаковые целые степени катетов какого-либо прямоугольного треугольника в сумме всегда меньше такой же степени его гипотенузы при n >2:
zn = xn0 + yn0 + ln (4)
где λn = zn-1[(k - kn-2)+(l - ln-2)] - неотрицательное действительное число, такое, что λn > 0, когда n > 2 и x0y0 ≠ 0, иλn=0, когда n = 2 и x0 y0≠0; x0, y0 € [0,z], z €(0, ∞).
Далее из (4) и рис 1 можно извлечь важную информацию о взаимнооднозначном соответствии множества разбиений {z2 = x20 + y20} и множества разбиений
{zn = xn0 + yn0 +λn}. Введя понятие прямоугольно-треугольного числа [11], можно удостовериться в том, что квадраты сторон прямоугольных треугольников рис. 1, измеряемых в прямоугольных числах, будут выражаться целыми числами, при этом площадь треугольника ОАВ равняется сумме площадей подобных треугольников ОСВ и АСВ. Таким образом, от несчетных множеств разбиений числа zn в действительных числах можно перейти к счетным множествам разбиений числа zn в прямоугольно-треугольных числах. С этого момента собственно и начинается доказательство ВТФ.
Предполагаемое решение уравнения Ферма в целых числах приравнивается одновременно двум разбиениям числа zn, находящимся на двух независимых направлениях, но принадлежащих одному и тому же конкретному разбиению уравнения Ферма (1) в целых числах. Из сравнения этих разбиений находится, что разбиение (1) в целых числах было бы верным, если бы уравнению (1) отвечало бы новое решение в меньших целых числах. Эту цепочку рассуждений можно продолжать до бесконечности в сторону уменьшения целых чисел, однако, осознав тот факт, что счетное множество натуральных чисел имеет своим нижним пределом натуральную единицу, приходится делать вывод о том, что решений уравнения Ферма в целых числах не существует. Такова краткая схема нативного доказательства ВТФ, детально изложенного в [11].
4. Заключение.
Таким образом, имеется доказательство ВТФ, элементарное по средствам исполнения, но далеко не элементарное по основополагающим идеям, глубоко коренящимся в очевидных геометрических построениях «фермаскопа». Чтобы продемонстрировать читателям хотя бы дух этих идей (именно дух, а не их инструментальное обоснование, которое пока еще далеко не исследовано), отметим удивительную способность «фермаскопа» давать вывернутую наизнанку картину прямоугольных треугольников, не выходя за пределы одной плоскости. Эту способность можно ярко отобразить на геометрической фигуре рис. 2, представляющей даосский символ Инь-Ян и называемой по-китайски (в русской транскрипции) Тао Цзы, и провести нативное доказательство ВТФ без каких-либо принципиальных изменений на инверсионной картине «фермаскопа».
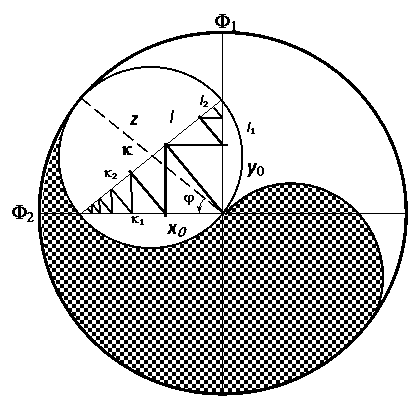
Рис. 2
Главная геометрическая особенность внутренней структуры Тао Цзы, раскрытой «фермаскопом», заключается в том, что концы диаметров двух малых кругов, вращающихся вокруг их общего центра при переменном угле φ, движутся с переменными скоростями по взаимно перпендикулярным прямым Ф1 и Ф2 , тогда как сами малые окружности катятся по внутренней стороне большого круга без скольжения (остальные обозначения на рис. 2 те же, что и на рис. 1 и в формулах (3)).
Итак, ВТФ сильна именно своим реальным содержанием, раскрывающимся в новых геометрических откровениях, а не пустыми теоретико-числовыми манипуляциями, ничего не меняющими по существу и которых вокруг уравнения Ферма можно придумать великое множество. К сожалению, чисто формальный и поверхностный подход к великой проблеме, которая одна может радикально изменить вектор развития фундаментальных наук, культивируется и насаждается сверху ответственными работниками науки и образования (см. [3]). Логику таких горе-ученых хорошо выразил один профессиональный математик в своем высказывании о теории относительности (см. [5]):
«Кое-кто утверждает, что ОТО
(а некоторые добавляют: и СТО) - самая большая ошибка ХХ века... Но даже если ошибка, то она сейчас так отшлифована, что лучше всякой правды. К тому же, еще не известно, от чего больше пользы.»
А что может быть «лучше правды» ? Только ложь ! Потому что именно она приносит дивиденды тем нечестным ученым, которые выдают желаемое за действительное, пользуясь безграмотностью или полной некомпетентностью статистов и заказчиков их сомнительных достижений. Поэтому скажем великое спасибо теореме Ферма еще и за то, что она помогла обнажить трофические язвы современной науки, а заодно и посмеяться над теми, кто из всего непонятного и загадочного устраивает жалкий фарс, за гримасами которого скрывается обыкновенное человеческое невежество.
СПИСОК ЛИТЕРАТУРЫ:
- http://dxdy/velikaya-teorema-ferma
- Ивлиев Ю.А. Ошибочное доказательство Уайлса Великой теоремы Ферма - Фундаментальные исследования (раздел «Физико-математические науки») 2008 № 3, 13-16.
- Ивлиев Ю.А. Величайшая научная афера ХХ века: «доказательство» Последней теоремы Ферма - Естественные и технические науки (раздел «История и методология математики») 2007 № 4(30), 34-48.
- Ивлиев Ю.А. Главный научный миф современности как диверсия против естественных наук и математического образования - Фундаментальные исследования (раздел «Физико-математические науки») 2008 № 8, 10-17.
- Ивлиев Ю.А. О качестве преподавания математики учащейся молодежи - Успехи современного естествознания (раздел «Педагогические науки») 2009 № 10, 53-55.
- Мухин Ю. О чем сыр-бор - в кн.: В. Бояринцев Антиэйнштейн. Главный миф ХХ века М.: Яуза 2005, 5-22.
- Дальма А. Эварист Галуа. Революционер и математик. Пер. с франц. под ред. Ю.И. Мерзлякова. М.: Наука, 1984.
- Ивлиев Ю.А. Великая теорема Ферма и современные математические науки - Научное обозрение. М.: Наука 2009 № 2, 53-55.
- Крафт Х. Алгебраические кривые и диофантовы уравнения - в кн.: Живые числа. Пер. с нем. Е.Б. Гладковой. М.: Мир, 1985, 87-104.
- Ивлиев Ю.А. Великая теорема Ферма и современная наука - Фундаментальные исследования (раздел «Физико-математические науки») 2009 № 5, 14-16.
- Ивлиев Ю.А. Реконструкция нативного доказательства Великой теоремы Ферма - Объединенный научный журнал (раздел «Математика») 2006 № 7(167), 3-9.



