В данной статье рассмотрим, как и для чего можно использовать матрицы в экономике, как решаются некоторые экономические задачи, анализируются и делаются из них определенные выводы.
Как известно, матрицей размераназывается прямоугольная таблица, содержащая m строк и n столбцов, в ячейках которой расположены элементы произвольного заранее выбранного множества – это могут быть целые, действительные или комплексные числа, векторы, рациональные функции – в зависимости от приложений и задач.
Матрицы получили широкое применение в математике потому, что благодаря их использованию, можно компактно записыватьразличные данные, системы линейных алгебраических илидифференциальных уравнений и т.д. В случае систем число уравнений соответствует количеству строк матрицы, а количество неизвестных – количеству столбцов. В результатезаписи систем линейных уравнений с помощью матриц их решение сводится к операциям над матрицами.
Понятие матрицы и матричная алгебра – математическая дисциплина, посвященная правилам действий над матрицами – имеют довольно большое значение для экономистов. Это обусловлено тем, что большая часть математических моделей экономических объектов и процессов записывается в довольно простой, а главное – компактной матричной форме.
С помощью матриц удобно записывать некоторые экономические зависимости. Для примера рассмотрим таблицу распределения ресурсов по отдельным отраслям экономики (условных единиц):
|
Ресурсы |
Отрасли экономики |
|
|
Машиностроение |
Строительство |
|
|
Электроэнергия |
7,3 |
4,1 |
|
Трудовые ресурсы |
4,8 |
8,2 |
|
Водные ресурсы |
2,7 |
5,1 |
Мы можем записать её в более компактной форме в виде матрицы распределения ресурсов по отраслям:
.
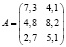Отсюда, матричный элемент a11=7,0 показывает, сколько электроэнергии расходует машиностроение, а элемент a22=8,2 – сколько трудовых ресурсов требуется строительной отрасли.
Для наглядности перейдём к рассмотрению задач.
Предположим, предприятие выпускает продукцию трёх видов: P1, P2, P3 и использует сырье двух типов: S1 и S2. Нормы расходаэтого сырья характеризуются следующей матрицей
,
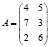в которой каждый элемент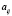 
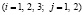показывает, сколько единиц сырья j-го типа расходуется на производство единицы продукции i-го вида. План выпуска продукции задан матрицей-строкой.
А стоимость единицы каждого типа сырья (денежных единиц) – матрицей столбцом:
.
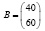Отсюда получаем, что затраты на первое и на второе сырьё составляют:
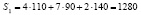единиц
и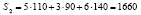 
единиц,
поэтому можем записать матрицу-строку затрат сырья S как произведение:
.
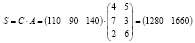Значит, общая стоимость сырья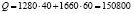 
денежных единиц тоже может быть записана в матричном виде:
.
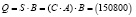Так же общую стоимость сырья можно вычислить и в другом порядке: для начала необходимо вычислить матрицу стоимостей затрат сырья на единицу продукции, то есть:
.
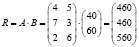А после этого общую стоимость сырья:
.
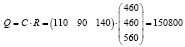На этом примере мы наблюдаем выполнение ассоциативного закона произведения матриц: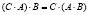 
.
Множество экономических задач можно свести к системам линейных уравнений. Для наглядного примера рассмотрим следующую задачу.
Мебельная фабрика специализируется на выпуске трех видов изделий: диванов, кресел и кроватей. При этом используется сырье трех типов: S1, S2, S3. Нормы расхода каждого этого сырья на один вид изделий и объем его расхода на один день заданы таблицей:
|
Виды сырья |
Нормы расхода сырья на одно изделие, условных единиц |
Расход сырья на 1 день, условных единиц |
||
|
Диваны |
Кресла |
Кровати |
||
|
S1 |
3 |
0 |
2 |
180 |
|
S2 |
1 |
4 |
1 |
160 |
|
S3 |
6 |
0 |
3 |
330 |
Чему равен ежедневный объем выпуска каждого вида изделия?
Решение сведём к системе линейных уравнений.
Пусть ежедневно фабрика выпускает x1. диванов, x2 кресел, x3 кроватей. Тогда в соответствии с расходами на сырьё изделий каждого вида, получим систему:
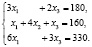
Эту систему можно решать различными методами. Мы применим метод Крамера, для чего составим и вычислим главный определитель системы
.
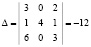Так как он отличен от нуля, то система совместна, а значит, имеет единственное решение. Составим и вычислим вспомогательные определители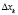 
, где 
:
, 
, 
.
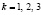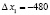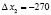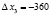Применяя формулы Крамера, получим решение задачи с точки зрения математики:
, 
,
.
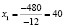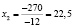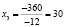Учитывая, что решение задачи должно быть целочисленным, из полученных значений переменных системы приходим к выводу, что ежедневно мебельная фабрика выпускает 40 диванов, 22 кресла и 30 кроватей.
Проанализировав применение матричной алгебры в экономике, можно прийти к выводу, чтоиспользование матриц имеет свои достоинства и недостатки.
Недостатки. Они заключаются в том, чтоматричная алгебра не обеспечивает реальных рекомендаций по разработке специфических стратегий; по матрицам невозможно определить сферы бизнеса, которые готовы стать победителями.
Достоинстваприменения матриц в следующем:
– они используют широкий набор стратегически значимых переменных; указывают направление движения ресурсов;
– позволяют с минимальными затратами труда и времени обрабатывать огромный и весьма разнообразный статистический материал, различные исходные данные, характеризующие уровень, структуру, особенности социально-экономического комплекса.
При наличии отрицательных моментов применения матричной алгебры положительная часть значительно обширнее.
Из выше рассмотренного можно сделать вывод:роль матриц в экономике очень и очень велика. Ведь благодаря их использованию можно гораздо быстрее, чем с использованием какого-либо другого математического аппарата, и проще решить многие экономические задачи, что чрезвычайно важно для экономистов.
Библиографическая ссылка
Немцова А.В., Попова С.В. ПРИМЕНЕНИЕ СРЕДСТВ МАТРИЧНОЙ АЛГЕБРЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ ЭКОНОМИЧЕСКОГО СОДЕРЖАНИЯ // Современные наукоемкие технологии. 2014. № 5-2. С. 171-172;URL: https://top-technologies.ru/ru/article/view?id=34049 (дата обращения: 04.11.2025).