При ежегодном распределении учебной нагрузки преподавателей, или научно-педагогических работников (НПР), кафедры параллельно возникает проблема, относящаяся к соблюдению вузовских юридических норм по планированию количества учебной работы для отдельных работников в индивидуальных планах (ИП). Используя обозначения автора [1], эту проблему можно сформулировать так: в общем случае одну часть такой учебной работы (именуемой нагрузкой) надо оформить в ИП как штатную (основную) нагрузку Ss, другую – как нагрузку по совместительству Sv, еще одну часть – как почасовую нагрузку Sc, и последнюю часть – как учебные поручения Su. Существуют также частные случаи, когда по разным причинам какие-либо из перечисленных форм ИП отсутствуют, а также существует пятая форма ИП – по договорам гражданско-правового характера, но в таком случае остальные формы исключаются.
Вышеуказанная проблема существует в различных вузах России, поэтому ей уделено внимание в ряде научных работ, например Д.А. Ивахненко [2], однако она не сообщает о программной реализации предлагаемого подхода. С 2017 г. А.Г. Смольяновым [3] используется информационная система «РасчетРаспределение», но она учитывает только Ss и Sc, а применяемый алгоритм не излагается.
В ФГБОУ ВО «ЧГУ им. И.Н. Ульянова» используется программное средство [4], при этом решение указанной проблемы производится методом проб и ошибок вручную, что влечёт умственные трудозатраты и значительную задержку. Необходимо учитывать, что некоторые нормы нельзя превышать, для некоторых норм в общем случае нельзя планировать меньшие значения, а также следует исходить из доли ставки. Например, на кафедре компьютерных технологий должно выполняться: для профессора Ss ∈ [800, 820], для старшего преподавателя Ss ∈ [880, 900] (единица измерения – академические часы). Если ставка неполная, эти размеры умножаются на долю ставки, например на 0,25. Подобные нормы и правила существуют и в других вузах [5]. Одна из причин: согласно Приказу Минобрнауки России [6], в вузах должно выполняться требование Ss ≤ 900.
В соответствии с нормами в [1] выделены ограничения и критерии оптимальности, на этой основе сформулирована целевая функция F для задачи дискретной оптимизации
F = F(O1,…,OC) → min,
где C – число элементов нагрузки; Oi (где i = 1,…,C) принимает четыре значения (от 0 до 3) – это номер разновидности ИП для i-го элемента нагрузки. Выражение для целевой функции учитывает 15 различных правил, включающих штрафные функции. По данным 2023–2024 учебного года, C может достигать 41. Таким образом, в данной задаче комбинаторной оптимизации для некоторых преподавателей существует 4C = 441 ≈ 4,8 ∙ 1024 комбинаций распределения нагрузки. Вероятно, существует возможность решить эту задачу переборным методом, возможно, с привлечением суперкомпьютеров, однако это чрезвычайно трудозатратно и ориентировочно оценивается в сотни миллионов долларов при аренде суперкомпьютера. В связи с этим в указанной статье предлагался более простой способ: применение генетического алгоритма (ГА) типа Genitor и машинного обучения.
Однако в некоторых случаях с помощью ГА не удаётся получить оптимального решения данной задачи, либо время её решения может достигать значительных величин – до нескольких минут.
Целью работы является разработка способа перераспределения учебной нагрузки для каждого НПР между ИП различных форм, который позволял бы осуществлять это за меньшее время, чем ГА, и не хуже последнего. Решаемые задачи: разработка алгоритма оптимизации, разработка программного средства, проведение и анализ результатов вычислений.
Материалы и методы исследования
Исследование проводится на основе сведений об учебной нагрузке на кафедре компьютерных технологий за последние 10 лет. Для исследования применяются такие методы, как анализ, метод сравнения, метод измерения, усреднение значений и вычислительный эксперимент. В качестве основы для разработки программного обеспечения используется программное средство [1].
Разработка алгоритма оптимизации целевой функции
Для оптимизации распределения часов между ИП можно использовать разные алгоритмы. Очевидно, что имеет смысл использовать наиболее эффективные из них. ГА применяется широко для решения разнообразных задач, однако для решения некоторых задач дискретной оптимизации более эффективен алгоритм оптимизации последовательности отбора (АОПО), например в 2021 г. это было показано автором по отношению к задаче составления расписания [7]. Поэтому далее используется рассмотренная в 2019 г. автором разновидность АОПО на основе схемы Коши, которую можно считать более эффективной среди других разновидностей [8]. В качестве последовательности отбора будет использоваться последовательность отбора элементов нагрузки для назначения вида ИП. АОПО применяет алгоритм имитации отжига, который был представлен в 1983 г. Векки, Киркпатриком и Гелаттом [9], и соответствующую терминологию.
Параметры алгоритма, используемые по умолчанию:
- исходное число итераций It = 500;
- увеличение числа итераций за шаг изменения температуры d = 280;
- число объектов последовательности, обменивающихся положением X = 1;
- исходная температура t = 5;
- делитель общего числа итераций (для определения числа шагов) DS = 25.
Используются переменные: C – число элементов нагрузки; O – массив видов ИП из C элементов; s – массив, представляющий собой последовательность отбора.
Алгоритм следующий.
1. Считывание параметров: d, X, t, It, DS.
2. Присвоить t1 ← t; t2 ← t; It1 ← 0; It2 ← 0.
3. Вычислить
.
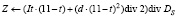4. Если не установлен флажок «Продолжение» (см. ниже), то получить близкий к оптимальному вариант, сохраняемый в массиве O, и начальную последовательность, сохраняемую в массиве s из C элементов. Для этого выполнять C раз следующее:
4.1. Присвоить номерам ИП Oi ← –1, где i = 1,…,C. Примечание: значение –1 означает, что вид ИП «недопустим»; тогда при вычислении F полагается, что соответствующей нагрузки нет.
4.2. Цикл k от 1 до C:
4.2.1. Цикл i от 1 до C: Если Oi = –1, то
4.2.1.1. Элементу Oi присваивать значения от 0 до 3, при этом вычисляя разность значений F после и до присвоения, и запоминая в Min тот вид, при котором разность минимальна по всем i, а в i1 – соответствующее i.
4.2.1.2. Присвоить Oi ← –1.
4.2.2. Зафиксировать Min в Oi1 и присвоить sk ← i1.
5. Скопировать массив s1 из s.
6. Вычислить исходное значение F :
min2 ← F(O).
7. Повторять следующие действия:
7.1. Присвоить fr ← 0.
7.2. Пока fr < It, выполнять следующие действия.
7.2.1. Присвоить fr ← fr + 1.
7.2.2. Скопировать массив s2 из s.
7.2.3. Совершить X раз обмен двух случайно выбранных элементов массива s.
7.2.4. Присвоить Oi ← –1, где i = 1,…,C.
7.2.5. Последовательно каждому элементу массива O присваивать значения от 0 до 3, при этом вычисляя F, и зафиксировать то значение, при котором F минимальна.
7.2.6. Присвоить min8 ← F(O); It2 ← It2 + 1.
7.2.7. Если It2 mod Z = 0, то It1 ← It1 + 1.
7.2.8. Присвоить t1 ← t2 / (1 + It1).
7.2.9. Если min8 ≤ min2 или
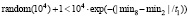, то:
7.2.9.1. Если min8 ≤ min2, то:
7.2.9.1.1. Присвоить min2 ← min8.
7.2.9.1.2. Если min2 ≤ 0, то присвоить fr ← It.
7.2.9.1.3. Скопировать массив s1 из s.
7.2.10. В противном случае (п. 7.2.9.) скопировать массив s из s2.
7.3. Если min2 ≤ 0, то присвоить t ← 10.
7.4. Присвоить t ← t + 1; It ← It + d.
7.5. Если t > 10, то перестать повторять и перейти к следующему пункту.
8. Скопировать массив s из s1.
9. Присвоить Oi ← –1, где i = 1,…,C.
10. Последовательно каждому элементу массива O присваивать значения от 0 до 3, при этом вычисляя F, и зафиксировать то значение, при котором F минимальна. Конец.
В результате вычислений в массиве O будет находиться искомое распределение номеров элементов нагрузки по видам индивидуальных планов.
При наличии алгоритма имеет смысл оценить его качество. Одним из критериев качества алгоритма является временная сложность. Временная сложность предложенного алгоритма рассчитывается, учитывая временные сложности отдельных шагов следующим образом:
- п.п. 1–3, 6 – константы по временной сложности;
- п. 4.2.1 – O(C), так как имеется цикл от 1 до C вычислений F по 8 раз. Вычисление F относительно трудоемко, так как учитывает 15 указанных правил, для каждого из которых производятся арифметические операции, операции сравнения и, возможно, изменение итоговой суммы, однако имеет временную сложность – константу;
- п. 4.2 – O(C2), так как имеется цикл от 1 до C выполнений п. 4.2.1, а сложность п. 4.2.2 – константа;
- п. 4 (получение близкого к оптимальному варианта) – O(C3), так как имеется цикл от 1 до C выполнений п. 4.2, а сложность п. 4.1 – O(C).
- п.п. 5, 8, 9 – O(C), причем без вычислений F по 4 раза.
- п. 10 – O(C) вычислений F.
- п. 7: количество повторений действий, совершаемых в этом пункте, может быть довольно велико и задаваться пользователем. По умолчанию – 7200, однако нередко происходит прекращение повторений в связи с достижением нулевого значения F. Это число повторений не зависит от C и, таким образом, может считаться константным значением. Однако сами действия имеют временную сложность, зависящую от C, которая составляет O(C) и рассчитывается следующим образом.
- п.п. 7.1, 7.3, 7.4, 7.5 – константы.
- п.п. 7.2.1, 7.2.3, 7.2.4, 7.2.7, 7.2.8 – константы, не требующие вычисления F.
- п. 7.2.5 – константа при вычислении четырех раз F.
- п. 7.2.6 – константа при вычислении F.
- п. 7.2.2 – O(C).
- п.п. 7.2.9.1.1, 7.2.9.1.2 – константы, не требующие вычисления F.
- п. 7.2.9.1.3 – O(C), так как копируется C элементов массива.
- п. 7.2.9.1 – сложность складывается, как показано выше, из констант и O(C), и составляет O(C).
- п. 7.2.9 – сложность соответствует сложности п. 7.2.9.1 и равна O(C).
- п. 7.2.10 – O(C), так как копируется C элементов массива.
- п. 7.2 – O(C), так как учитываются константы и O(C) входящих в его состав подпунктов.
Таким образом, временная сложность алгоритма равна O(C3), однако такое выражение формируется только при получении исходного, близкого к оптимальному, варианта. Практически наибольшее время занимает работа по п. 7, сложность которого O(C). Это время зависит от параметров d, t, It.
Используемые программные средства
Для реализации предложенного алгоритма добавлена функциональность к Windows-приложению [1], обрабатывающему данные, предварительно извлеченные из базы данных системы «Кафедра» [4]. Пользователю теперь нужно выбрать соответствующий алгоритм оптимизации, а остальные действия аналогичны действиям в предыдущей версии.
По такому же принципу, как в [1], применялось машинное обучение для оптимизации параметров ГА, в новой версии приложения машинное обучение используется для оптимизации параметров АОПО. При этом оптимизируются параметры Ds и X. Предусмотрен вывод на экран промежуточных и конечных значений. Результаты машинного обучения сохраняются в отдельном файле.
Пользователь может установить флажок «Продолжение» для того, чтобы при следующем нажатии на кнопку «АОПО» оптимизация начиналась не заново, а с точки, достигнутой к данному времени в текущем сеансе.
Результаты исследования и их обсуждение
Чтобы сделать выводы об эффективности применения АОПО, производилось сравнение времени его работы со временем работы ГА для соответствующих ИП, которое требуется для получения F = 0 при изначальном F ≠ 0. В качестве исходных данных рассматривались данные по 225 ИП. Приблизительно в 42% случаев нагрузка относилась только к одному виду ИП, и перераспределять её не требовалось. В около 12% случаев условие F = 0 не достигалось за длительное время, в связи с чем для них дальнейший анализ не проводился, однако программа позволяет разделять элементы нагрузки на самостоятельные элементы по усмотрению пользователя, затем оптимизируя обычным образом. Для 6 нагрузок значение F = 0 достигалось только с помощью АОПО, но не ГА, что говорит в пользу предлагаемого алгоритма: нулевое значение достигается чаще, а не реже, чем с помощью ГА.
В итоге при сравнительном анализе учитывалось примерно 44% случаев. Каждая нагрузка оптимизировалась с помощью обоих алгоритмов, по 10 раз с целью получения усреднённых данных. Обозначим как R = VA / VG соотношение скорости оптимизации с помощью АОПО к скорости при использовании ГА для соответствующего ИП. Для исследования R использованы подходы математической статистики.
Данные по 97 ИП о среднем соотношении скоростей
|
R > 0,01; R > 100 |
R > 0,1 |
R > 0,1 |
R > 1 |
R > 1 |
R > 1 |
R > 1 |
R > 10 |
R > 10 |
R > 10 |
|
0,050776 |
0,22052 |
0,30856 |
4,3863 |
9,3746 |
1,5290 |
1,5512 |
19,062 |
56,264 |
20,371 |
|
0,028772 |
0,47376 |
0,13060 |
4,4755 |
5,8720 |
4,4963 |
8,4725 |
12,032 |
45,870 |
10,340 |
|
0,093969 |
0,26003 |
0,91518 |
2,5542 |
5,1175 |
6,1344 |
1,8622 |
11,377 |
10,134 |
39,327 |
|
– |
0,40241 |
0,38078 |
1,7604 |
2,6249 |
1,1026 |
1,6243 |
16,227 |
25,764 |
13,690 |
|
– |
0,27876 |
0,59112 |
1,6911 |
2,2600 |
2,1948 |
3,8834 |
11,261 |
27,833 |
77,579 |
|
– |
0,81129 |
0,50777 |
2,8899 |
8,1246 |
2,1342 |
9,7215 |
91,914 |
11,356 |
39,572 |
|
– |
0,33499 |
0,69174 |
9,8183 |
1,9519 |
1,1119 |
2,5377 |
14,485 |
12,166 |
33,063 |
|
– |
0,24217 |
0,17344 |
4,1131 |
1,0439 |
4,9228 |
2,3027 |
24,815 |
62,320 |
10,351 |
|
198,14 |
0,54698 |
0,15796 |
5,7542 |
2,7154 |
3,7032 |
4,5445 |
13,488 |
15,156 |
34,012 |
|
141,16 |
0,13668 |
0,11467 |
2,9741 |
5,8943 |
3,2529 |
1,8031 |
|||
|
125,52 |
– |
– |
5,0390 |
2,7480 |
4,0965 |
3,2766 |
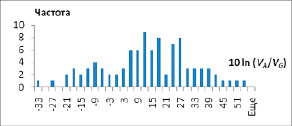
Гистограмма распределения данных о величине 10lnR
В таблице приводятся значения R для каждого из рассмотренных ИП (среднее арифметическое по серии из 10 испытаний).
Как следует из таблицы, в 74 случаях из 97, т.е. примерно в 3 случаях из 4, R > 1, т.е. скорость работы АОПО выше.
Далее, анализируя данные таблицы, можно найти, что коэффициент эксцесса примерно равен 17,5, а коэффициент асимметрии 3,91. По этим показателям полученное распределение далеко от нормального, где они равны 3 и 0 соответственно. Для оценки доверительного интервала с применением распределения Стьюдента нужно, чтобы распределение было более близким к нормальному. Для этого, в соответствии с рекомендациями [10, с. 153], выполнено логарифмическое преобразование: от данных взят натуральный логарифм и умножен на 10. Средним значением стало 12,24, коэффициент эксцесса –0,279, коэффициент асимметрии –0,211. Это значительно ближе к значениям нормального распределения, что подтверждается также формой гистограммы (рисунок).
У доверительного интервала для математического ожидания совокупности с нормальным (Гауссовским) распределением, основанного на выборке из n наблюдений, обозначаемых X1, X2,…, Xn, когда критическая область двусторонняя и неизвестно среднеквадратическое отклонение, границы равны [11, с. 326]:
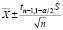, (1)
где 
,
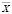– среднее значение величины по наблюдениям, tn–1,1–α/2 – α%-ные точки распределения Стьюдента с (n – 1) степенями свободы, α – уровень значимости.
Доверительная вероятность не превышает (100 – 2α)%. Применяя формулу (1) и используя 1,96 – квантиль для доверительной вероятности 0,95, находим доверительный интервал для доверительной вероятности 0,95, составляющий 3,73. Т.е. математическое ожидание величины 10lnR находится в пределах 8,51 … 15,97. Путём обратного преобразования получено: exp(8,51/10) ≈ 2,34; exp(15,97/10) ≈ 4,94. Таким образом, с доверительной вероятностью 0,95 можно утверждать, что истинное среднее значение математического ожидания R находится в пределах от 2,34 до 4,94.
Рассматривая вышеприведенную таблицу и отбрасывая два крайних значения, можно также заключить, что область значений, в которой находится R с вероятностью 98% – от 0,0508 до 141,16. То есть, как правило, АОПО может работать в 20 раз медленнее ГА, а может в 141 раз быстрее, и в среднем быстрее в 3,64 раза.
Заключение
Для оптимизации распределения нагрузки НПР между его ИП АОПО успешно применен. Вычислительный эксперимент показал, что этот алгоритм для данной задачи приблизительно в 3,6 раза более эффективен по времени, чем ГА. Измерения времени показывают, что среднее арифметическое времени работы исследуемого алгоритма на обычном персональном компьютере составляет 2–3 секунды.
Библиографическая ссылка
Димитриев А.П., Лавина Т.А. ПРИМЕНЕНИЕ АЛГОРИТМА ОПТИМИЗАЦИИ ПОСЛЕДОВАТЕЛЬНОСТИ ОТБОРА ДЛЯ РАСПРЕДЕЛЕНИЯ УЧЕБНОЙ НАГРУЗКИ ПРЕПОДАВАТЕЛЯ ПО ИНДИВИДУАЛЬНЫМ ПЛАНАМ // Современные наукоемкие технологии. – 2024. – № 4. – С. 15-20;URL: https://top-technologies.ru/ru/article/view?id=39967 (дата обращения: 19.05.2024).