В настоящее время для решения задач оптимизации и управления используются хорошо разработанные методы, которые, как правило, основаны на использовании одного из двух допущений [1, 2]:
− рассматриваемый объект или процесс рассматриваются с детерминистических позиций;
− рассматриваемый объект или процесс рассматриваются со статистических или стохастических позиций.
Первое приводит к тому, что полностью отсутствуют источники неопределенности, второе – к тому, что неопределенности имеют место, но вместе с этим известны их статистические или стохастические характеристики, что достаточно сложно себе представить при изучении реальных технологических объектов или процессов.
Еще один из путей, позволяющих выполнить формализацию неопределенностей с целью их дальнейшего использования при построении математических моделей, основан на применении интервального анализа. В настоящее время хорошо известны методы решения задач оптимизации и управления, построенные на основе его использования [3, 4].
При этом методы, основанные на использовании интервального анализа, не позволяют использовать качественную информацию при построении математических моделей, что, с одной стороны, существенно ее обедняет, а с другой, снижает ее адекватность.
Таким образом, обоснованным является предположение о необходимости использования как на этапе моделирования, так и на этапе решения соответствующих задач оптимизации и управления интеллектуальных методов, основанных на применении теории нечетких множеств, для формализации неопределенностей и необходимой качественной информации.
Материалы и методы исследования
В достаточно общем виде математическая модель рассматриваемого процесса или объекта представляет собой систему операторных уравнений, которая имеет вид
y� = M(x�, u, b�), (1)
где М – оператор нечеткой математической модели; x�, b� – элементы соответствующих нечетких подмножеств 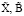 ; y� – нечеткая выходная величина.
; y� – нечеткая выходная величина.
Математическую модель, позволяющую определить функцию принадлежности 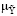 (y | u) в зависимости от детерминированного значения управляющего воздействия u и функций принадлежности
(y | u) в зависимости от детерминированного значения управляющего воздействия u и функций принадлежности 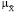 (x) и
(x) и 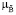 (b), запишем в виде
(b), запишем в виде
 (y | u) = М (
(y | u) = М (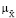 (x), u,
(x), u, 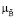 (b)),
(b)),
где М – оператор математической модели с заданным набором свойств, 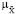 (x), u,
(x), u, 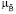 (b) – соответствующие функции принадлежности элементов подмножеств,
(b) – соответствующие функции принадлежности элементов подмножеств, 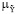 (y | u) – функция принадлежности нечеткого решения.
(y | u) – функция принадлежности нечеткого решения.
Определим оператор М, положив в основу определение функции принадлежности нечеткого решения принцип расширения Заде, следующим образом:
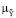 (y | u) =
(y | u) = 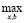 min (
min (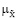 (x),
(x), 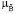 (b)) | y = M (x, u, b),
(b)) | y = M (x, u, b),
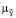 (y | u) = 0, если {(x, u, b) | y = M (x, u, b)} = ∅,
(y | u) = 0, если {(x, u, b) | y = M (x, u, b)} = ∅,
где М – детерминированная математическая модель.
Так как выходная величина y становится нечеткой, то размытой величиной становится и значение функции технологических требований ji (x, y, u).
Нечеткое подмножество значений ji (x, y, u) будем характеризовать функцией принадлежности 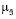 (ji | u ), зависящей от управления u и связанной с
(ji | u ), зависящей от управления u и связанной с 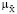 (х),
(х), 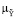 (y | u) оператором вида
(y | u) оператором вида
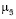 (ji | u ) = y (
(ji | u ) = y (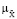 (x),
(x), 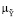 (y | u)).
(y | u)).
Определим функцию принадлежности технологических требований следующим образом:
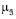 (ji | u) =
(ji | u) = 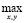 min (
min (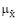 (x),
(x), 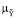 (y | u)) | ji = ji (x, y, u),
(y | u)) | ji = ji (x, y, u),
x ∈ X, u ∈ U, y ∈ Y,
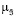 (ji | u) = 0, если {(x, y, u) | ji = ji– (x, y, u)} = ∅.
(ji | u) = 0, если {(x, y, u) | ji = ji– (x, y, u)} = ∅.
Целевая функция также становится нечеткой величиной и определяется функцией принадлежности, которая зависит от управления u.
Будем обозначать функцию принадлежности целевой функции 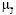 (J | u) и определять ее по формуле
(J | u) и определять ее по формуле
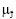 (J | u) =
(J | u) = 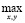 min (
min (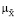 (x),
(x), 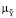 (y | u)), | J = J (x, u, y),
(y | u)), | J = J (x, u, y),
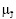 (J | u) = 0, если {(x, u, y) | J = J– (x, u, y)} = ∅.
(J | u) = 0, если {(x, u, y) | J = J– (x, u, y)} = ∅.
В условиях нечеткости выходной величины задача оптимизации может быть поставлена как задача нахождения вектора u*∈U управляющих воздействий, при котором некоторая норма функции принадлежности целевой функции ║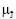 (J | u)║ принимает оптимальное значение и при этом гарантируется, что функция принадлежности технологических требований ji будет подтверждать выполнение этих требований с «достаточной убедительностью».
(J | u)║ принимает оптимальное значение и при этом гарантируется, что функция принадлежности технологических требований ji будет подтверждать выполнение этих требований с «достаточной убедительностью».
Такую задачу назовем задачей гарантирующей оптимизации в условиях неопределенности. В этих условиях необходимо формализовать гарантированность с «достаточной убедительностью» выполнения технологических требований.
Предлагается считать, что i-е технологические требования выполняются с «гарантией», если
∀ji ≤ ai : 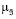 (ji | u) < ei ;
(ji | u) < ei ;
$ ji : 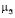 (ji | u) ≥ ei , i =
(ji | u) ≥ ei , i = 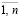 ,
,
где ei – постоянная величина, так называемый «уровень существенности».
Назовем областью существенности Ei множество ji, таких, что
Ei = { ji | 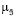 (ji | u) ≥ ei }.
(ji | u) ≥ ei }.
Назовем границей существенности jiг значений ji число, определяемое по формуле
jiг(u) = 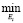 ji.
ji.
Сформулируем задачу гарантирующей оптимизации в условиях неопределенности следующим образом: необходимо найти u* из некоторого u*∈Uд, при котором принимает минимальное значение целевая функция Q(u):
Q* = Q (u*) = 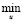 Q (u), (2)
Q (u), (2)
где Q(u) = min J | 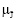 (J | u) ≥ μЗ ,
(J | u) ≥ μЗ ,
при гарантированном удовлетворении технологических требований для i = 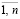
jiг (u) ≥ ai, i = 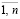 , (3)
, (3)
где jiг (u) = 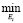 ji,
ji,
Ei = { ji | 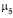 i (ji | u) ≥ ei },
i (ji | u) ≥ ei },
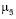 i (ji | u) =
i (ji | u) = 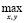 min (
min (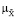 (x),
(x), 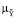 (y | u)) | ji = ji (x, y, u),
(y | u)) | ji = ji (x, y, u),
и удовлетворении уравнений математической модели
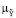 (y | u) =
(y | u) = 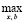 min (
min (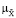 (x),
(x), 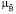 (b)) | y = M (x, u, b). (4)
(b)) | y = M (x, u, b). (4)
Управление u*, найденное при решении задачи (2)–(4), будем называть гарантирующим оптимальным управлением.
Решение задачи гарантирующей оптимизации в форме (2)–(4) сопряжено со значительными трудностями многократных вычислений, как уравнений математической модели М, так и систем ограничений, обусловленных необходимостью расчета функций принадлежности выходных величин и технологических параметров по известным функциям принадлежности входных величин.
Рассмотрим декомпозиционный метод, который будем называть a-оптимизацией [5, 6].
Введем вектор α = (a1, a2, …, an), где n – число технологических требований, а также моды х и b нечетких величин x� и b�.
Назовем a-задачей следующую задачу.
a-задача.
Необходимо найти вектор uопт∈U управляющих воздействий, при котором принимает минимальное значение целевая функция J (х, u, y)
J* = 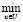 J (х, u, y),
J (х, u, y),
где y = М (х, u, b),
при удовлетворении технологических требований
ji (х, y, u) ≥ ai, i = 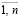 . (5)
. (5)
Чтобы подчеркнуть зависимость оптимального значения целевой функции J* от a, будем его в дальнейшем обозначать J*(a).
Оптимальное управление uопт, найденное при решении a-задачи, так же как и целевая функция, зависит от значения a. Обозначим это управление uaопт.
В качестве математической модели М может быть использован оператор М, определенный в (1), где вместо x� и x� следует использовать моды х, b. Однако могут быть случаи, когда М целесообразнее заменить более простым оператором, если он будет обладать соответствующими свойствами.
Будем называть множество управлений
Uα = {u | u∈U ∧ ji (x, y, u) ≥ ai,
i = 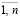 ∧ y = М (х, u, b)}
∧ y = М (х, u, b)}
множеством a-допустимых управлений.
Управление u∈Uα будем называть a-допустимым.
Тогда a-задача может быть сформулирована следующим образом.
Необходимо найти вектор uαопт∈Uα управляющих воздействий, при котором принимает минимальное значение J*(α) целевая функция J (х, u, y)
J*(α) = min J (х, u, y). u∈Uα
Математически задача нахождения оптимального α ставится следующим образом.
Необходимо найти такое значение α*∈Θ, при котором принимает минимальное значение целевая функция J*(α)
α* = arg 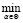 J*(α),
J*(α),
где величина J*(α) определяется решением a-задачи:
uaопт = arg 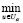 J (х, u, y),
J (х, u, y),
Uα = { u | u∈U ∧ ji (х, y, u) ≥ ai,
i = 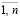 ∧ y = М (х, u, b)},
∧ y = М (х, u, b)},
J*(α) = J (х, uопт, y).
Область Θ (область гарантированного удовлетворения технологических требований) определяется следующим образом:
Θ = {α | uaопт ∈ Ŋ }. (6)
Значение α∈Θ будем называть Θ-допустимым значением α.
Оптимальное управление uaопт∈Uα, соответствующее Θ-допустимому α, будем называть Θ-допустимым оптимальным управлением.
Значение ua*опт∈Uα* является оптимальным управлением, найденным в результате решения задачи a-оптимизации.
Рассмотрим условия тождественности задач гарантирующей оптимизации в условиях неопределенности и α-оптимизации. При принятых обозначениях сформулируем следующую теорему.
Теорема. Пусть задача гарантирующей оптимизации в условиях неопределенности (ЗГО) имеет решение и пусть модели M (х, u, b), М (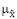 (x), u,
(x), u, 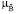 (b)) и функционалы Q (u), ji (х, y, u) таковы, что для любых u1, u2 ∈ U выполняются следующие отношения:
(b)) и функционалы Q (u), ji (х, y, u) таковы, что для любых u1, u2 ∈ U выполняются следующие отношения:
[J (х, u1, y) | y = M (х, u1, b)] > [J (х, u2, y) | y = M (х, u2, b)] ⇒
⇒ [Q (u1) = (min J |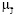 (J | u1) > μЗ)] > [Q (u2) = (min J |
(J | u1) > μЗ)] > [Q (u2) = (min J | 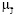 (J | u2) > μЗ)] ,
(J | u2) > μЗ)] ,
ji (х, y, u1) ≥ ji (х, y, u2) ⇒ jiг (u1) ≥ jiг (u2).
Тогда существует решение задачи a-оптимизации, и оно совпадает с решением задачи гарантирующей оптимизации в условиях неопределенности.
Доказательство. Обозначим u* – решение задачи гарантирующей оптимизации в условиях неопределенности (2)–(4).
Таким образом, для всех u∈U выполняется
Q (u*) < Q (u), (7)
где U – множество u, удовлетворяющих (3),
U = { u | jiг (u) ≥ аi, i = 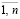 }. (8)
}. (8)
Так как существует такая a*-задача, что ее решение совпадает с решением ЗГО, т.е. ua* = u*.
Таким образом, J (х, u*, y) ≤ J (х, u, y) для всех u∈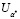 .
.
При этом, так как u* является решением ЗГО, по определению (6) удовлетворяется условие jiг (u*) ≥ аi, i = 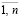 , и так как
, и так как 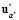 = u* , то
= u* , то 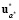 ∈Q.
∈Q.
Таким образом, множество Q не пустое и решение задачи a-оптимизации существует. Докажем, что это решение совпадает с решением задачи a-оптимизации.
Допустим, что это не так, то есть существует некоторое 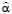 ∈ Q, такое, что для решения
∈ Q, такое, что для решения 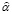 -задачи выполняется соотношение
-задачи выполняется соотношение
J (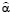 ) < J (α*). (9)
) < J (α*). (9)
Так как 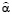 ∈Q, то по определению αi = ji (х, y, u*), i =
∈Q, то по определению αi = ji (х, y, u*), i = 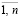 , выполняется условие
, выполняется условие
jiг(uα*) ≥ аi, i = 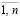 , то есть решение
, то есть решение 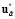
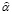 -задачи принадлежит допустимому множеству Ŋ задачи ЗГО, определяемой (2)–(4).
-задачи принадлежит допустимому множеству Ŋ задачи ЗГО, определяемой (2)–(4).
Очевидно, что
Jc (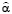 ) = J* (х,
) = J* (х,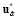 ,
,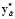 ),
),
Jc (α*) = J*(х, 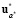 ,
, 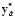 ),
),
где 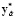 = M (
= M (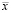 ,
, 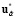 ,
, 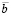 ),
),
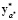 = M (
= M (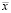 ,
, 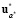 ,
, 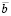 ).
).
Таким образом, из (9) имеем
J* (х, 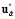 ,
, 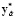 ) < J* (х,
) < J* (х, 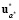 ,
, 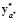 ). (10)
). (10)
По условию теоремы из (10) следует Q (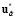 ) < Q (
) < Q (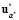 ), что невозможно, так как
), что невозможно, так как 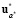 = u* и является решением ЗГО в условиях неопределенности. Теорема доказана.
= u* и является решением ЗГО в условиях неопределенности. Теорема доказана.
Предлагается итерационный алгоритм решения задачи гарантирующей оптимизации в условиях неопределенности, который заключается в следующем.
1. Вводятся начальные значения вектора a.
2. Решается a-задача с использованием детерминированной модели M (x, u, b).
3. Для найденного a-допустимого значения управления ua с использованием модели М проверяется выполнение технологических требований.
4. При невыполнении технологических требований происходит коррекция составляющих вектора a для которых гарантированность выполнения требований нарушена.
5. Если технологические требования соблюдены, то проверяется целесообразность дальнейшего уточнения (улучшения) допустимого управления.
6. Если поиск оптимального управления необходимо продолжить, то корректируются составляющие вектора a, для которых технологические требования выполнены.
Математическая формализация нечетких величин и параметров осуществляется соответствующими функциями принадлежности. Предложен алгоритм построения функций принадлежности выходных величин.
В блоке 1 блок-схемы вводится значение управляющего воздействия u, для которого необходимо построить реакцию: функцию принадлежности μ (y).
Блок 2 – организует цикл перебора x и b.
Блок 3 – для каждого xj и bk определяет соответствующие значения функции принадлежности μ (xj) и μ (bk) и минимальное значение из этих двух величин aijk: aijk = min [ μ (xj), μ (bk)].
Блок 4 – вычисляет yijk, соответствующее заданным значениям u, xj, bk по математической модели y = M (u, x, b).
Блок 5 – запоминаются значения yijk и aijk, формируя таблицы Y и A.
Блок 6 – определяет окончание цикла перебора x и b.
Таким образом, в блоках 2–6 рассчитываются и запоминаются все возможные yijk для заданного u и соответствующие им aijk.
Блок 7 – организует цикл перебора y и определяет для каждого из них значение функции принадлежности μ(yi).
Блок 8 – определяет интервал величиной 2Di, где Di – заданная точность расчета такая, что принадлежность y этому интервалу идентифицируется как значение y = yi.
Блок 9 – находит из заполненной таблицы Y = {yijk}, значения yijk∈[yi, yi ], где yi = yi – ∆i, yi = yi + ∆i и идентифицирует их как yi.
Блок 10 – для каждого из найденных yijk выбирается из таблицы А соответствующее значение aijk.
Таким образом, формируется множество aijk, соответствующих yi.
Блок 11 – определяет значение функции принадлежности μ(yi), соответствующее значению yi по формуле μ (yi) = 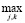 aijk.
aijk.
Блок 12 – определяет окончание цикла.
Если цикл окончен, то функция принадлежности μ (y) для заданного значения u построена.
Заключение
В работе получены условия, обеспечивающие выполнение технологических требований с заданным уровнем гарантии. Это привело к необходимости постановки задачи гарантирующей оптимизации химико-технологических процессов в условиях неопределенности и разработки методов ее решения. Получены теоретические результаты в виде необходимых и достаточных условий тождественности задачи гарантирующей оптимизации в условиях неопределенности и последовательности детерминированных задач в зависимости от заданного уровня гарантии альфа. Для решения последовательности детерминированных оптимизационных задач, решение которых обеспечивает достижение заданного уровня гарантии, предложен итерационный алгоритм. Применение предложенного подхода, суть которого заключается в замене оптимизационной задачи в условиях неопределенности, последовательностью детерминированных оптимизационных задач, обеспечивает сокращение времени получения результата. Результаты, полученные в данном исследовании, подтверждают результаты исследований процесса производства обесфторенных фосфатов.
Библиографическая ссылка
Громов Ю.Ю., Погонин В.А. НЕЧЕТКОЕ УПРАВЛЕНИЕ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ // Современные наукоемкие технологии. – 2023. – № 10. – С. 26-31;URL: https://top-technologies.ru/ru/article/view?id=39787 (дата обращения: 19.05.2024).



