Психологами установлено, что чем дольше обучающийся занимается решением какой-либо проблемы и подходит к ее разрешению с разных сторон, тем более прочно откладываются в его сознании все сопутствующие знания, которые актуализируются для решения этой проблемы [1]. А если постановка и решение проблемы отыскиваются самим обучающимся и он сам собирает необходимые данные, то материал, с которым работает учащийся, надолго запечатлевается в его сознании. Поэтому так важно включать в систему занятий лабораторно-практические работы, организовывать экскурсии на предприятия малого бизнеса с целью сбора информации и постановки задач.
Лабораторно-практические работы способствуют осуществлению внутрипредметных и межпредметных связей математики, делая знания старшеклассников цельными и формируя в их сознании целостную картину мира. Экскурсии реализуют связи с жизнью, практикой, предоставляя материал для математической интерпретации жизненных ситуаций [2]. Поэтому лабораторно-практические работы и экскурсии способствуют повышению уровня математической подготовки выпускников общеобразовательной школы, формированию целостного мировоззрения, позволяют усилить прикладную направленность обучения математике и помочь школьникам определить свою профессиональную ориентацию [3]. В качестве математического материала нами выбраны дифференциальные уравнения по ряду причин:
- дифференциальные уравнения являются непосредственным продолжением содержательной линии «Уравнения» школьного курса математики;
- для изучения этого материала школьной математикой созданы все предпосылки: учащиеся знакомы с понятиями производной, дифференциала, первообразной, интеграла, их геометрическим и механическим смыслом, свойствами, простейшими дифференциальными уравнениями с разделяющимися переменными, и это означает, что материал вполне доступен для усвоения школьниками;
- дифференциальные уравнения используются при решении задач из самых разных областей человеческой деятельности и областей знания (химии, медицины, экономики и т.д.), а одному из основных методов математики, а именно методу математического моделирования, в школе уделяется недостаточное внимание;
- на решение достаточного числа практико-ориентированных задач в рамках общеобразовательной школы учебного времени явно не хватает, поэтому знакомство с дифференциальными уравнениями целесообразно продолжить в системе дополнительного образования [4; 5, с. 1].
Полноценное изучение дифференциальных уравнений в школе проблематично как с точки зрения психологии, так и с точки зрения методики преподавания математики. Но основные определения и алгоритмы раздела обучающимся будут понятны [6].
Цель исследования состоит в теоретическом обосновании проблемы изучения элементов теории обыкновенных дифференциальных уравнений в системе дополнительного образования на основе практико-ориентированного подхода с использованием метода математического моделирования и разработке ее методического обеспечения.
Материалы и методы исследования
Работа проводится на материале дифференциальных уравнений на основе практико-ориентированного подхода.
Теоретические методы: сравнительный анализ научной, педагогической, учебно-методической литературы, направленный на определение содержания и логики исследования; изучение нормативной документации по обучению математике в средней общеобразовательной школе, системе дополнительного образования.
Эмпирические методы, связанные с исследованием практики преподавания в дополнительном образовании: диагностика состояния знаний учащихся с помощью контрольных работ и тестов, педагогическое наблюдение, беседы, анкетирование, интервьюирование, изучение и обобщение практики и опыта работы учителей математики средней школы и педагогов дополнительного образования, анализ собственного опыта преподавания, проведение эксперимента.
Результаты исследования и их обсуждение
Подходящих сюжетов для создания проблемной ситуации, формулирования проблемы и последующего её решения с привлечением изученного материала можно найти немало в любой местности. Это может быть бизнес по выпечке хлеба (частные предприятия «Жар-свежар», «Горячий хлеб» «Булка» и др.), статистические данные о числе жителей в городах и поселках, экономические сюжеты (например, на спрос и предложение), сюжеты на основе анализа механического движения (скорость моторной лодки и др.), на остывание нагретого предмета (хлеба, чайника и пр.), на количество выдыхаемого людьми в замкнутом помещении углекислого газа, на концентрацию используемого в домашнем консервировании рассола, сахарных сиропов и мн. др. Самое главное заключается в том, что числовые данные для составления задач учащиеся могут собрать сами, совершив экскурсию на предприятие малого бизнеса и побеседовав с его владельцем, а также непосредственно произведя измерения исследуемых величин для лабораторной работы (причем такие измерения старшеклассники могут проделать в домашних условиях, а на занятии заняться их обработкой), получив их из статистических источников (опубликованных статистических данных в газетах, бюллетенях и т.п.) или в результате социального опроса. Активность познавательной деятельности – важный фактор заинтересованности учащихся в учении, способствующей формированию целостного мировоззрения, целостного взгляда на окружающий мир, так как так организованное обучение показывает учащимся единение разнообразных знаний (экономических, экологических, физических, математических и др.) и единство способов их достижения (двигательных, умственных, коммуникативных и пр.) [7]. Особую роль при формировании единой картины мира играет математическое содержание, поскольку многие задачи из разных областей знания и практической деятельности человека решаются посредством создания той или иной универсальной математической модели [8–10].
Приведем примеры.
Чтобы у учащихся было достаточно материала для составления задачи о выпечке хлеба, целесообразно организовать экскурсию на одну из частных пекарен (такие есть в любой местности). В предварительной беседе с учащимися необходимо нацелить их на содержание вопросов, которые они будут задавать владельцу пекарни. Учащиеся в рамках дискуссии выясняют, что нужно узнать стоимость единицы выпекаемого хлеба (булки, буханки), количество продаваемого в течение единицы времени (например, суток) хлеба, величину направляемой на расширение пекарного дела выручки, влияние увеличения (удвоения, например) вложений в дело на увеличение (скорость) выпечки хлеба. В результате получается следующая матрица задачи: Хлебопекарня посёлка выпекает и продаёт … буханок хлеба в … стоимостью … рублей за одну буханку. В течение месяца … % выручки от реализации хлеба направляется на расширение производства. Известно, что … вложений в производство приводит к увеличению скорости выпечки хлеба в … раз. Сколько буханок хлеба в день будет выпекать пекарня к концу месяца?
После экскурсии задача пополняется числовыми данными.
С задачами с однозначно понимаемым условием, имеющими вполне определённое и находимое по определённому правилу единственное решение, учащиеся имеют дело на протяжении всех лет обучения в средней школе [11, с. 24].
Задача, как известно, развивает логическое мышление обучающихся, учит умению анализировать условия, выделять главный вопрос, определять неизвестное и находить пути их решения, она является важнейшим элементом в математической подготовке обучающихся. Практико-ориентированные задачи, кроме того, знакомят обучающихся со связью между процессами и явлениями реального мира и его математическими моделями [5, с. 3, 11, с. 27].
Дифференциальное уравнение, полученное в результате исследования какого-либо реального процесса (явления), называется дифференциальной моделью этого процесса (явления). Мы будем рассматривать лишь модели, описываемые так называемыми обыкновенными дифференциальными уравнениями [12].
Задача 1. Хлебопекарня посёлка выпекает и продаёт тысячу буханок хлеба в сутки стоимостью 8 рублей за одну буханку. В течение месяца 3 % выручки от реализации хлеба будет направляться на расширение производства. Известно, что удвоение вложений в производство приводит к увеличению скорости выпечки хлеба в полтора раза. Сколько буханок хлеба в день будет выпекать пекарня к концу месяца [13]?
Учащиеся задумываются над её решением:
Пусть y(t) – количество испечённого в момент времени t хлеба, причём время измеряется в сутках. Выручка от его реализации составит 8y рублей, из которых 0,03•8y = 0,24y рублей направляется на расширение производства, что приводит к увеличению скорости выпечки хлеба y′ в полтора раза и составит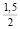 
•0,24y = 0,18y раз. Учащиеся получают уравнение с разделяющимися переменными y′ = 0,18y и находят его общее решение: y = ce0,18t. Далее школьники используют начальные условия, т.е. решают задачу Коши. Из условия y(0) = 1000 находят с = 1000. Остаётся подставить t = 30 суток, чтобы получить окончательный ответ: y(30) = 1000e5,4 ≈ 221406 буханок хлеба. Учащиеся получают приблизительное число буханок, а это показывает им, что на практике точные значения получаются не всегда.
Ответ: 221406 буханок.
С учащимися следует обсудить полученный результат. Ответ задачи показывает, что если даже не очень большую часть прибыли постоянно вкладывать в производство дефицитного товара, то очень быстро можно добиться огромного роста объёма его выпуска (экспоненциальный рост). Данная модель является весьма упрощённой и редко наблюдается в реальности, так как в ней не учитываются, например, насыщение рынка и износ оборудования.
Задачи на концентрацию растворов также отнесём к той категории, которая предполагает предварительные экскурсии с целью сбора данных или сбор данных другими способами. Можно провести экскурсию на местный консервный завод и там собрать нужные данные. А можно провести социальный опрос. Например, пригласить на занятие 2–3 родителей, которые занимаются консервированием в домашних условиях или провести организованную экскурсию всей группы обучающихся к нескольким родителям. Ведь многие хозяйки, в том числе и родители учащихся, занимаются домашним консервированием, заготавливают соленья и варенья на зиму. В связи с этим учитель просит учащихся собрать у родителей нужные данные для составления задач, решаемых методом дифференциальных уравнений. Учащиеся, как показывает практика, приносят много составленных ими на полученном материале задач. Каждый учащийся обрабатывает свои данные на занятии в рамках лабораторно-практической работы. Затем можно предложить им следующую задачу.
Задача 2. В резервуаре имеется 100 л рассола, содержащего 10 кг растворенной соли. Каждую минуту 2 л рассола вытекает из резервуара, а 3 л пресной воды притекает в него. Перемешивание сохраняет одинаковую концентрацию соли в резервуаре. Сколько соли останется в резервуаре через час [14]?
Решение. Учащиеся обозначают через x – количество соли в резервуаре, через t – время, отсчитываемое от начального момента в минутах. За промежуток времени dt из резервуара уходит (–dx) кг соли (ведь икс – убывающая функция времени, значит, dx – отрицательная величина, а (–dx) – положительная). Чтобы составить уравнение, школьники вычисляют убыль соли иным путем. В момент t в резервуаре находится (100 + t) л жидкости (притекло 3t л и утекло 2t), в ней растворено x кг соли. Значит, в одном литре рассола содержится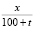 
кг соли. За время dt из резервуара вытекает 2dt литра рассола, значит, количество соли уменьшится на 
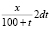кг.
Получают дифференциальное уравнение
.
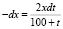Затем учащиеся решают полученное дифференциальное уравнение. Разделяя переменные и учитывая начальные условия t0 = 0, x0 = 10, получают:
,
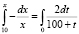т.е.
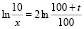
или
.
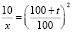Подставляя t = 6 в последнее равенство, находят искомое количество соли x ≈ 3,91 (кг).
Ответ: 3,91 кг.
Целесообразно помочь учащимся осмыслить решение этой задачи, привести теоретическое обоснование. Для данного исследования было применено обыкновенное дифференциальное уравнение с разделяющимися переменными, имеющее вид
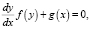
которое решается следующим образом:
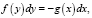
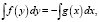
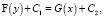
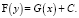
Следующий тип задач, сюжеты которых можно получить с помощью социального опроса или из опыта, это задачи, связанные с техникой, транспортом и т.п. У многих школьников в семьях есть моторные лодки, и учащиеся вместе с родителями выезжают на природу. В связи с этим учитель, предложив им решить представленную ниже задачу о моторной лодке, даёт задание составить другие задачи о скорости своей моторной лодки, решаемые методом дифференциальных уравнений, взяв данные непосредственно из измерения (опытным путём) или узнав у родителей.
Задача 3. Катер двигался по озеру со скоростью 32 км/ч, и через 1 минуту, после того как был выключен двигатель, его скорость стала равной 8 км/ч. Чему будет равна скорость катера через 2 минуты после остановки двигателя, если сопротивление воды пропорционально скорости движения катера? Какое расстояние он пройдёт через 1 минуту после выключения мотора? Какое расстояние он пройдёт через 2 минуты после выключения мотора [5, с. 4, 13]?
При решении этой задачи учащиеся пользуются межпредметными связями, в данном случае
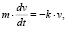(1.1)
которое является математической моделью, описывающей движение катера. Разделяя переменные и интегрируя, учащиеся получают общее решение:
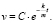(1.2)
Учитывая начальные условия, школьники получают
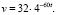(1.3)
Таким образом, скорость катера через 2 мин =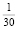 
ч после остановки двигателя будет равна 2 км/ч.
Обозначая через S = S(t) расстояние, которое катер будет проходить после остановки двигателя, в силу механического смысла производной учащиеся имеют по (1.3):
S’ = 32•4–60t,
Откуда, интегрируя и учитывая, что S(0) = 0, получают
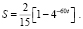(1.4)
При t = 1 мин =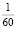 
ч из (1.4), имеем
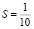(км),
т.е. через 1 мин после остановки двигателя катер пройдёт 100 м.
При t = 2 мин =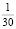 
ч из (1.4) имеем
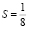(км),
т.е. через 2 мин после остановки двигателя катер пройдёт 125 м.
Ответ. Через 2 мин после остановки двигателя скорость катера будет 2 км/ч, и он пройдёт расстояние 125 м, а через 1 мин после остановки двигателя он пройдёт расстояние 100 м.
Учащиеся могли предложить воспользоваться хорошо известной формулой S = v•t, где v определяется по формуле (1.3), но она привела бы к ошибочным парадоксальным результатам: через минуту пройденное после остановки двигателя расстояние равнялось бы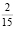 
км, а через 2 минуты – 
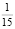км, т.е. расстояние бы уменьшилось, что невозможно. Здесь нужно обратить внимание учеников, что формула S = v•t справедлива для равномерного движения и в данном случае неприменима [5, с. 4].
На данных о транспорте или другой технике, собранных учащимися у родителей или знакомых, учителю целесообразно провести лабораторную работу. Она будет индивидуальной или на двух учащихся. Учащиеся должны быть информированы о порядке выполнения лабораторной работы и получить письменную инструкцию об этом. В инструкции должны быть пункты: тема, цель работы, собранные данные, теоретические основы, порядок выполнения работы: составление задачи, подбор математической модели, решение дифференциального уравнения, интерпретация результата, выводы.
Приведём ещё типы задач, которые могут лечь в основу практико-лабораторных работ. Данные для сюжетов, аналогичных задаче 4, учащиеся получают в домашних условиях или на занятии. Эксперимент с чайником может проделать каждый учащийся.
Задача 4. Скорость остывания воды в чайнике пропорциональна разности температуры чайника и кухни. Чайник выключился в 10.20 при температуре воды 100 °С. В 10.30 температура воды в чайнике была 80 °С. Найти время, за которое температура воды в чайнике будет равна 40 °С, если температура на кухне 20 °С [14].
Решение несложно и приводит учащихся к ответу: t ≈ 1 час.
Анализ решения показывает, что с течением времени t температура чайника не может стать ниже 20 °С, т.е. ниже температуры воздуха на кухне, и выше 100 °С. Таким образом, анализ полученных формул показывает учащимся, что они адекватно описывают (математически моделируют) процессы, рассматриваемые в подобных задачах.
Решив предложенную учителем задачу 5, учащиеся могут сделать аналогичные расчеты для комнаты в своём доме или квартире.
Задача 5. В воздухе комнаты объёмом 200 м3 содержится 0,15 % углекислого газа (CO2). Вентилятор подаёт в минуту 20 м3 воздуха, содержащего 0,04 % CO2. Через какое время количество углекислого газа в воздухе комнаты уменьшится втрое [15]?
В задачах о росте населения чаще всего известны исходное количество населения и время прироста, а искомым является конечное количество населения. Данные для составления таких задач берутся из газет, журналов, интернета. С учащимися на занятии решается задача в общем виде, т.е. с буквенными данными. В результате обучающиеся получают зависимость в общем виде (формулу), пользуясь которой, они могут решать большое количество задач этого типа, в том числе самостоятельно составленных.
Задача 6. Пусть скорость прироста населения прямо пропорциональна его количеству. Найти зависимость между количеством населения А и временем t, если известно, что в некоторый момент принимаемый за начальный, количество населения равнялось А0 и через год оно увеличилось на а %.
В результате решения этой задачи учащиеся получают формулу зависимости количества населения от времени:
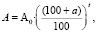
где а % – годовой прирост населения.
Учащимся интересно проследить рост населения Земли, например, с 1650 г. В 1650 г., условному началу промышленной революции, на Земле было примерно 500 млн чел. Более достоверные статистические данные о населении Земли можно найти примерно с 1800 г., они показывают, что за последние два столетия население возрастало с ускорением. По этим данным, увеличение от одного миллиарда человек до двух миллиардов произошло за 104 года, прирост следующего миллиарда жителей Земли произошёл за 36 лет, последующего – за 16 лет, от 4 до 5 млрд чел. народонаселение всех стран увеличилось за 9 лет. Можно предложить учащимся построить график динамики роста населения Земли.
Современный период – это продолжающийся экспоненциальный рост населения земного шара, в основном за счёт развивающихся стран Африки, Юго-Восточной Азии и Латинской Америки. В 2000 г. численность населения Земли достигла 6,1–6,2 млрд чел., в 2017 – 7,6 млрд чел., в 2025 г., по прогнозу демографов население Земли возрастёт до 8,3 млрд. чел., ещё через 50 лет можно ожидать 11 млрд чел., почти в два раза больше, чем сейчас. Учащиеся могут подсчитать дальнейший рост населения Земли, а также население своего города, района, посёлка.
Экономические задачи также представляют собой материал, который удобно реализовать на занятиях с предварительным проведением экскурсий или в форме лабораторных работ. При решении задач с экономическим содержанием (на спрос и предложение, на коммунальные платежи и др.) учитель решает ещё одну проблему – финансовой грамотности старшеклассников. Учащиеся знакомятся с содержанием экономических терминов, знание которых обязательно понадобится им, когда они вступят во взрослую жизнь [10]. Еще раз подтверждается тезис о необходимости формирования целостного мышления учащихся, целостных представлений о жизни на Земле, о единстве мира и единых законах, в нем действующих.
Задача 7. Функции спроса и предложения на некоторый товар имеют соответственно вид
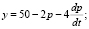
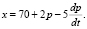
Найти зависимость равновесной цены от времени, если ????(0) = 10, и определить, является ли равновесная цена устойчивой.
Решение приводит учащихся к ответу: ???? = 15e4t – 5; не является.
Далее, обобщая полученный результат, можно предложить учащимся решить задачу в общем виде.
Рассмотрим практико-ориентированную задачу с физическим содержанием, которая была включена в ЕГЭ по физике в 2019 г.
Задача 8. Небольшой брусок массой m = 100 г, скользящий по гладкой горизонтальной поверхности, абсолютно неупруго сталкивается с неподвижным телом массой М = 2m. При дальнейшем поступательном движении тела налетают на недеформированную пружину, одним концом прикреплённую к стене (рисунок). Через какое время t после абсолютно неупругого удара бруски вернутся в точку столкновения? Скорость движения бруска до столкновения v = 2 м/с, жёсткость пружины k = 30 Н/м, а расстояние от точки столкновения до пружины L = 10 см.
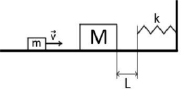
Решение:
1. В процессе абсолютного неупругого столкновения сохраняется суммарный импульс системы тел: mv = (m + M)v1, где v1 – скорость тел после столкновения.
2. Так как поверхность гладкая, то трения нет, и движение тел от момента удара до момента касания свободного конца пружины будет равномерным: L = v1t1, где t1 – время движения на этом участке.
3. После касания пружины и до отрыва от неё тела будут двигаться, совершая гармоническое колебание. До отрыва пройдёт время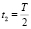 
, где T – период колебаний груза на пружине: 
.
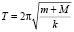Только в течение этого промежутка времени (от касания пружины и до отрыва от неё) движение будет ускоренным, потому что и до касания пружины, и после отрыва от неё движение будет равномерным – с постоянной скоростью. Ускоренное движение описывается дифференциальным уравнением. Найдём это дифференциальное уравнение следующим образом.
Движение на всём шаге 3 состоит из двух фаз: до максимального сжатия пружины и после него. Эти фазы абсолютно симметричны друг другу (просто движение происходит в противоположных направлениях), а значит, достаточно вычислить время первой фазы и умножить его на два. Это движение подчиняется закону Гука:
F = - kx,
где F – сила, k – жёсткость пружины, x – удлинение пружины (в действительности, в данной фазе не удлинение, а укорочение, потому что пружина сжимается).
Сила равна массе, умноженной на ускорение. Ускорение – это производная скорости, то есть вторая производная перемещения. А перемещение – это переменная x, потому что перемещается незакреплённый конец пружины. Значит, получаем уравнение
mx» + kx = 0,
где m и k – заданные постоянные (только, естественно, вместо m надо брать M + m, ведь сила упругости действует на единую систему «брусок вместе с телом»). Это уравнение – линейное обыкновенное дифференциальное уравнение второго порядка. Поскольку и масса, и жёсткость – величины положительные, его общее решение есть гармоническое колебание
x(t) = C1cos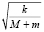
t + C2sin
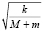t.
Чтобы найти значения этих двух произвольных постоянных, нам нужно два начальных условия. Первое из них – это x(0) = 0, потому что в начальный момент времени (а это момент столкновения с пружиной) никакого удлинения (укорочения) у пружины нет. А второе – это x′(0) = v1, потому что после столкновения тел друг с другом эта система «брусок вместе с телом» движется равномерно (с постоянной скоростью) до самого столкновения с пружиной. А v1 уже вычислено на первом шаге решения.
Таким образом, из первого начального условия находим, что C1 = 0, значит, решение выражается формулой
x(t) = C2sin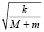
t.
Вычислим его производную:
x′(t) = C2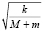 
cos
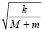t.
Подставив ее во второе начальное условие, получим, что
v1 = C2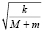
, то есть C2=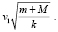 
Тогда окончательная формула для решения – следующая:
x(t) =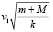 
sin
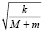t.
А окончательная формула для его производной (т.е. для скорости) – следующая:
x′(t) = v1cos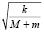
t.
Теперь, чтобы найти длительность ускоренной фазы движения, надо узнать, когда эта фаза закончится. Это произойдёт тогда, когда свободный конец пружины остановится (за счёт того, что её упругость полностью погасит импульс, приобретённый системой «брусок вместе с телом» до её столкновения с пружиной), то есть когда скорость обратится в нуль. Используя только что найденную формулу для скорости, приходим к выводу, что это произойдёт, когд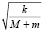 
t станет равным π/2, то есть в момент t = π/2
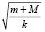. Но это длительность лишь половины ускоренной фазы движения. Во второй половине всё происходит симметрично – единственная разница заключается в том, что пружина не сжимается (укорачивается), а распрямляется (удлиняется); под действием тех же самых сил. Поэтому найденную длительность половины ускоренной фазы движения надо в итоге умножить на два: получи
.
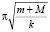4. Отрыв тел от пружины произойдёт в точке касания пружины. По закону сохранения механической энергии при гармонических колебаниях скорость тел в точке отрыва равна v1. Дальнейшее движение тел будет равномерным. Поэтому полное время движения тел до точки столкновения
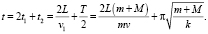
Учитывая, что M = 2m, получим
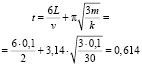с.
Ответ: t = 0,614 с.
Заметим, что поскольку в условиях общеобразовательной школы нет возможности проводить экскурсии и лабораторно-практические работы, требующие больше времени, чем может быть уделено в рамках обязательного общего образования, а целостное представление о мире, в котором он живёт, необходимо будущему активному члену общества, то становится ясной необходимость такой работы в системе дополнительного образования.
В результате проведенных занятий у учащихся повысился интерес к изучению математики, потому что они увидели ее практическую значимость. Это показали результаты анкетирования школьников экспериментальной и контрольной групп.
С целью выяснения отношения старшеклассников к предлагаемому им для изучения разделу и сформированности у них представлений о целостности окружающего мира было проведено два анкетирования в начале и в конце эксперимента. Анкета содержала представленные ниже 5 вопросов.
1. Знакомы ли вы с понятием дифференциального уравнения?
2. На каких знаниях базируется решение дифференциальных уравнений?
3. Умеете ли вы решать дифференциальные уравнения?
4. Применяются ли на практике, в жизни дифференциальные уравнения?
5. Хотите ли вы научиться решать дифференциальные уравнения?
В контрольной группе ответы старшеклассников на вопросы анкеты до и после эксперимента отличались незначительно, а в экспериментальной группе замечены существенные различия: значительно увеличилось число учащихся, ответивших утвердительно на 4 и 5 вопросы.
В начале эксперимента учащимся контрольной и экспериментальной групп предлагалась самостоятельная работа, в которой задачи базировались на знаниях учащихся, полученных в соответствии со школьной программой (производная, геометрический и механический смысл, первообразная, интеграл и др.). Результаты выполнения этой самостоятельной работы оказались примерно одинаковыми в контрольной и экспериментальной группах.
В конце эксперимента школьникам контрольной и экспериментальной групп предлагалась самостоятельная работа, содержащая 5 заданий, каждое из которых позволяло выявить наличие у обучающихся определённых умений устанавливать связи между конкретными ситуациями и математическим аппаратом (в данном случае, с дифференциальными уравнениями).
Самостоятельная работа
1. Составить понятийную карту для дифференциальных уравнений с разделяющимися переменными.
2. Известно, что скорость размножения некоторых бактерий пропорциональна количеству бактерий в данный момент с коэффициентом пропорциональности k. Определить k, если в 10 часов в сосуде было 2 000 бактерий, а в 12 часов уже 32000.
3. Составить задачу по дифференциальному уравнению
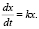
4. На основании данных, полученных во время экскурсии в хозяйство индивидуального предпринимателя, составить задачу, решаемую с помощью дифференциального уравнения.
5. Опытным путём получить зависимость укорочения (растяжения) мышцы руки при поднятии тяжестей.
Учащиеся контрольной группы знали, что собой представляет понятийная карта (составляли, например, для понятия четырёхугольник). С учителем контрольной группы было обговорено, что для выполнения задания 4 он даст им необходимые данные без организации экскурсии, а задание 5 в контрольной группе не выполняли. Таким образом, сравнение результатов двух групп делалось по четырём заданиям.
Анализ результатов самостоятельной работы в контрольной группе показал, что с первой задачей учащиеся в целом справились; при решении второй и четвертой испытывали затруднения, потому что представили решение с существенными недочётами и порой с ошибками; третью задачу решили немногие учащиеся. Задача 5 им не предлагалась. Самое главное, учащиеся не связывали решение предложенных задач с математической моделью ситуаций – дифференциальными уравнениями.
В экспериментальной группе обучающиеся справились в основном со всеми задачами, допустив некоторые негрубые ошибки и недочёты. Итогом проведенных занятий стало приобретённое школьниками умение математизировать ситуации, возникающие в повседневной жизни, и разрешать их методом дифференциальных уравнений, т.е. они демонстрировали некоторое понимание целостности окружающего мира и единства действующих в нем законов. Об этом свидетельствуют результаты контрольных работ в начале и конце исследования.
Выводы
Проведённое исследование показало, что изучение элементов дифференциальных уравнений в системе дополнительного образования на основе практико-ориентированного подхода с применением метода математического моделирования позволяет не только повысить познавательный интерес старшеклассников к учению и качество их математических знаний, их целостность и целостность мировоззрения, но и способствует подготовке к адекватному выбору будущей профессии, более уверенной ориентации в жизни, что необходимо каждому выпускнику в его будущей профессиональной деятельности как активному члену общества.
Библиографическая ссылка
Лобанова Н.И., Аммосова Н.В. ЛАБОРАТОРНО-ПРАКТИЧЕСКИЕ РАБОТЫ И ЭКСКУРСИИ ДЛЯ СТАРШЕКЛАССНИКОВ В СИСТЕМЕ ДОПОЛНИТЕЛЬНОГО МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ // Современные наукоемкие технологии. – 2020. – № 11-1. – С. 152-160;URL: https://top-technologies.ru/ru/article/view?id=38355 (дата обращения: 21.11.2024).