Современные трубопроводы содержат системы труб, соединенные между собой многочисленными стыками, врезками и сварными соединениями. Расчет напряжений в этих соединениях представляет собой сложную научно-техническую задачу [1].
Вопрос о целесообразности рассмотрения труб как трехмерных тел был поднят в статье [2]. Были установлены пределы применимости стержневой и оболочечной моделей для проблемы туннелирования. В этом случае трубопровод представлял собой трехмерную структуру, окруженную внешней средой. Для задачи о подводном трубопроводе сравнение стержневой и оболочечной моделей выполнено в [3].
Если на трубе есть линия стыка с другой трубой, то решение уравнений теории упругости такой системы содержит сингулярность на этой линии, как указал А.Л. Гольденвейзер в [4]. Современным развитием этого направления является математическое моделирование трубопроводов как оболочек слабой регулярности [5]. В недеформированной геометрии моделируемой трубы сингулярность содержится в постановке задачи. В [5] показано, с какими трудностями сталкиваются математики при численном анализе таких задач.
Таким образом, задачи расчета напряженно-деформированного состояния трубопровода в приближении трехмерного тела актуальны.
Перед инженером возникает проблема выбора адекватного инструмента численного решения поставленных задач. Например, задача исследования взаимодействия изогнутой трубы и потока жидкости решалась при помощи пакета SolidWorks в [6]. Применение этого пакета к другим задачам детально изложено в [7].
Помимо коммерческих пакетов прикладных программ, существуют свободно распространяемые программы, сопоставимые с ними по качеству результатов. Одним из таких пакетов является FreeCAD [8]. С нашей точки зрения, FreeCAD можно рассматривать как визуальную оболочку для пакета решения задач методом конечных элементов CalculiX, который встроен во FreeCAD и также распространяется свободно.
Целью данной работы является создание алгоритма и анализ результатов численных экспериментов по расчету напряженно-деформированного состояния (НДС) трубопроводов с изломом и изгибом профиля в пакете прикладных программ FreeCAD.
Поставлены задачи:
1. Создание 3D-моделей труб во FreeCAD.
2. Создание алгоритма применения программного пакета метода конечных элементов (МКЭ) CalculiX в визуальной оболочке FreeCAD.
3. Построение сеток МКЭ программой NetGen в визуальной оболочке FreeCAD.
4. Численный анализ задач расчета НДС трубопроводов с изломом и изгибом профиля.
5. Визуализация результатов расчетов и анализ возможностей FreeCAD для их обработки.
6. Сравнение полученных результатов между собой и с литературными данными для оценки адекватности математического моделирования в среде FreeCAD.
Постановка задачи
Рассматриваются две задачи.
Задача 1. Труба с изломом профиля (рис. 1, а).
Механическая система представляет собой две трубы одинакового внутреннего радиуса Ri = 45 мм и толщины стенки h = 5 мм. Длина труб вдоль осей до точки их пересечения L1 = L2 = 250 мм. Они жестко соединены между собой под углом 90 ° и закреплены шарнирно на свободных концах. Изнутри на трубы действует равномерно распределенное давление p0 = 10 МПа. Трубы выполнены из стали S335JO (аналог 17Г1С) с параметрами материала: плотность ρ = 7800 кг/м3, модуль Юнга E = 210 ГПа, коэффициент Пуассона v = 0,3, σТ = 343 МПа, σВ = 490 МПа.
Задача 2. Труба с изгибом профиля (рис. 1, б).
Две трубы одинакового внутреннего радиуса Ri = 40 мм и толщины стенки h = 5 мм соединены коленом в виде сегмента тора с такими же параметрами. Осевые линии труб расположены под углом 90 ° и имеют длины L1 = 93 мм и L2 = 120 мм. Материал труб – сталь S335JO. Свободные концы труб закреплены жестко. Нагрузка на трубы такая же, как в задаче 1.
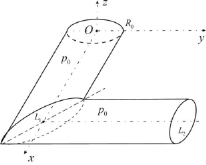
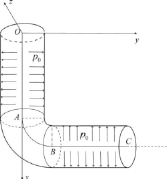
а) б)
Рис. 1. Геометрия системы труб: а) задача 1, б) задача 2
С математической точки зрения требуется найти численное решение системы уравнений Ламе теории упругости для трехмерного твердого тела в области, занятой трубой. На открытых торцах труб ставятся соответствующие условия закрепления, на внутренней поверхности трубы – условия равенства нормальных напряжений внешнему давлению, на внешней поверхности трубы – условия отсутствия напряжений. На линии контакта ставятся условия непрерывности перемещений и усилий. Подробности математической постановки задачи изложены в работе [9].
Согласно источникам [4, 5], в Задаче 1 должен наблюдаться рост напряжений в окрестности линии стыка труб. В Задаче 2 такого роста быть не должно, а только должно быть относительно небольшое повышение напряжения в окрестности закрепленных концов и в окрестности линий стыка тороидального и прямолинейного участков.
Материалы и методы исследования
Задачи 1, 2 решены в визуальной среде FreeCAD со встроенным решателем МКЭ CalculiX и построителем сеток NetGen.
Алгоритм решения задачи в среде FreeCAD:
1. Построение 3D-модели в среде FreeCAD согласно [8, 10]. Инструменты среды: Scetcher – для построения эскизов сечений и направляющих осевых линий труб; Part Design – формирование трехмерной модели на основе эскизов.
2. Формирование твердого тела по модели. Инструменты: модуль Part для формирования итоговой модели, проверки ее геометрии и окончательного преобразования в твердое тело.
3. Создание модуля конечно-элементного анализа и построение сетки. Инструменты модуля FEM: Analysis – создание и активация анализа; Mesh, FEM Mesh Netgen – построение сетки МКЭ на твердом теле.
4. Наложение граничных условий, приложение нагрузок и задание материала. Инструменты модуля FEM: Material for Solid – выбор материала из базы данных, Mechanical Constrains – наложение граничных условий и давления внутри трубы.
5. Генерация файла исходных данных и решение задачи. Инструменты: Solve, Solver job control: выбор типа анализа (static), генерация исходных данных (Write .inp file), нахождение численного решения (Run CalculiX).
6. Визуализация результатов. Инструменты: Results, Show Results.
Результаты исследования и их обсуждение
Задача 1. В пакете прикладных программ FreeCAD была построена математическая модель метода конечных элементов (МКЭ), изображенная на рис. 2 (сохранено из программы).
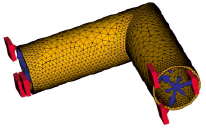
Рис. 2. Модель МКЭ, показана сетка метода, закрепления краев и направления нагрузки
На рис. 2 изображены способ закрепления границ трубы и направление давления внутренней среды. Параметры сетки МКЭ: число узлов – 31514, число поверхностей элементов – 10526, число объемных элементов – 15651. В результате вычислений по представленной выше методике найдено распределение напряжений, изображенное на рис. 3. На рис. 3, а, изображен градиент напряжений от максимального красного к минимальному зеленому.
На рис. 3, б, изображено распределение напряжений по количеству узлов сетки. Численные предельные значения напряжений и перемещений в задаче 1 приведены в табл. 1.
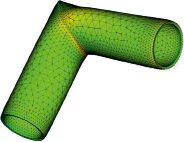
Задача 2. Модель МКЭ, построенная во FreeCAD, изображена на рис. 4.
На рис. 4, а, изображены направления действия внутреннего давления на трубу и способ закрепления краев трубы. На рис. 4, б, изображен общий вид сетки МКЭ; наблюдается сгущение узлов сетки в окрестности скачка кривизны оси трубы.
На рис. 5 графически представлены результаты численного анализа задачи о напряженно-деформированном состоянии изогнутой трубы.
На рис. 5, а, изображены напряжения по цветовым уровням: от максимального красного к минимальному зеленому. На рис. 5, б, изображено распределение напряжений по узлам сетки, из которого видно, что в большей части узлов сетки МКЭ напряжение составляет от 60 до 85 МПа. Численные значения напряжений и перемещений приведены в табл. 2.
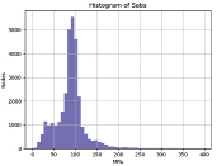
а) б)
Рис. 3. Распределение напряжений в трубе: а) графические изолинии, б) гистограмма
Таблица 1
Напряжения и перемещения в стыке труб
|
Физическая величина |
Максимальное |
Среднее |
Минимальное |
|
Эквивалентное напряжение по Мизесу |
395,5 МПа |
89,5 МПа |
2,9 МПа |
|
Абсолютное перемещение |
0,13 мм |
0,047 мм |
0,0 мм |
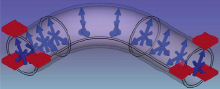
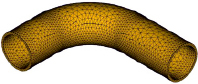
а) б)
Рис. 4. Расчетная модель МКЭ изогнутого профиля: а) нагрузки и закрепления, б) сетка МКЭ
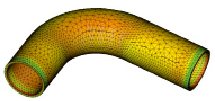
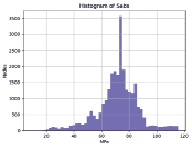
а) б)
Рис. 5. Напряжения в изогнутой трубе: а) графические изолинии; б) гистограмма
Таблица 2
Напряжения и перемещения в соединенных коленом трубах
|
Физическая величина |
Максимальное |
Среднее |
Минимальное |
|
Эквивалентное напряжение по Мизесу |
115,6 МПа |
72 МПа |
8,9 МПа |
|
Абсолютное перемещение |
0,039 мм |
0,018 мм |
0,0 мм |
При сравнении рис. 3, а, и рис. 5, а, видна разница в распределении напряжений в случае наличия и отсутствия линий излома поверхности трубы. В задаче 1 максимальные эквивалентные напряжения превышают предел пропорциональности σТ, хотя и находятся ниже предела прочности при растяжении σB. В задаче 2 ни один из этих пределов не превышен.
Разница в распределении напряжений по количеству узлов сетки МКЭ видна при сравнении гистограмм этих распределений на рис. 3, б, и рис. 5, б. Гистограмма на рис. 3, б, показывает, что предел пропорциональности превышен в относительно малом числе узлов сетки, в то время как значения напряжений в большем количестве узлов лежат в окрестностях среднего значения 89,5 МПа, указанного в табл. 1. Гистограмма на рис. 5, б, показывает более широкое распределение, в среднем дающее близкое к предыдущему значение напряжения 72 МПа.
Распределения перемещений в задачах 1 и 2 дают качественно похожие картины с распределениями напряжений. В задаче 1 также ярче выражено пиковое значение максимального перемещения 0,13 мм, указанное в табл. 1, которое распределено по небольшому числу узлов сетки в окрестности линии особенности. Распределение перемещений в задаче 2 имеет намного более гладкий вид, что показано в табл. 2, где разница между максимальным и средним значениями невелика.
При сравнении распределения напряжений в задаче 1 (рис. 3, а) с распределением напряжений в математически близкой задаче теории упругости с входящим углом, рассмотренной в статье [11], можно сделать вывод о близости этих распределений в качественном смысле. Задача из [11] дала ясный результат с концентрацией напряжений. Значит, распределение напряжений в трубах с угловым соединением, найденное по предложенному здесь алгоритму, является достоверным в качественном смысле.
Необходимо обсудить вопрос о количественной достоверности полученных в пакете FreeCAD численных результатов. Была решена задача Ламе о толстостенной трубе [12, c. 339], решение которой известно. Пусть длинная цилиндрическая труба из стали S335JO находится под действием внутреннего давления p0 = 10 МПа. Внутренний радиус трубы равен 100 мм, наружный – 150 мм, длина трубы – 2 м. Концы трубы закреплены от продольных перемещений и не закреплены от поперечных. Точное решение, найденное в [12, с. 339], дает максимальное эквивалентное напряжение по Мизесу, равное 31,4 МПа. Максимальное эквивалентное напряжение, полученное в пакете FreeCAD, равно 32,5 МПа. Таким образом, полученные численные результаты являются достоверными.
Заключение
Создан алгоритм математического моделирования трубопровода в пакете прикладных программ FreeCAD. Этот алгоритм предусматривает создание 3D-модели, построение сетки метода конечных элементов, подготовку исходных данных, постановку вычислительных экспериментов, визуализацию результатов расчетов.
Построены модели МКЭ для двух задач: задачи с сильной особенностью в виде линии излома поверхности трубы и задачи со слабой особенностью в виде линии скачкообразного изменения кривизны поверхности. Выполнены численные эксперименты, проведено сравнение результатов между собой и с литературными данными.
В итоге сравнения результатов между собой установлено, что в задаче с сильной особенностью эквивалентные напряжения по Мизесу меняются с большим градиентом в окрестности особенности, чем в задаче со слабой особенностью. Более того, в окрестности линии излома на внутренней стороне угла напряжения превышают предел текучести.
В итоге сравнения результатов с литературными данными установлено, что построенные математические модели адекватно описывают механическую систему как с качественной, так и с количественной точки зрения. Таким образом, пакет прикладных программ FreeCAD является надежным инструментом исследования трехмерных твердотельных моделей методом конечных элементов.
Численные эксперименты были проведены на вычислительном кластере ЦКП «Центр данных ДВО РАН».
Библиографическая ссылка
Ткаченко О.П. ВЫЧИСЛИТЕЛЬНОЕ МОДЕЛИРОВАНИЕ ТРУБОПРОВОДА С ИЗЛОМОМ ПРОФИЛЯ В ПАКЕТЕ ПРИКЛАДНЫХ ПРОГРАММ FREECAD // Современные наукоемкие технологии. 2020. № 11-1. С. 73-78;URL: https://top-technologies.ru/ru/article/view?id=38341 (дата обращения: 14.01.2026).
DOI: https://doi.org/10.17513/snt.38341



