С 2003 г. действует Федеральный закон № 177-ФЗ «О страховании вкладов в банках Российской Федерации», согласно которому физические лица, разместившие вклады в российских банках (далее – вкладчики), могут обратиться за получением страхового возмещения (до 1.4 млн рублей на одного вкладчика в одном банке) в случае отзыва у банка лицензии. Однако не все вкладчики пользуются данным правом, в результате чего определенные суммы остаются невостребованными.
В связи с этим возникает несколько вопросов.
- От чего статистически зависит факт обращения вкладчика за страховым возмещением?
- Можно ли спрогнозировать количество вкладчиков, которые обратятся за страховым возмещением?
- Можно ли спрогнозировать общую сумму денежных средств, которые не будут востребованы вкладчиками?
Ответы на эти вопросы могут дать математические модели, построенные на основе алгоритмов машинного обучения.
Материалы и методы исследования
В качестве исследуемого банка выберем кредитную организацию, лицензия которой была отозвана летом 2018 г. Его вкладчиками являлись около 118 тыс. граждан, открывших в совокупности 171 тыс. счетов, на которых было размещено свыше 17 млрд рублей – банк является относительно крупным по размеру среди банков с отозванной лицензией.
Любой алгоритм машинного обучения требует, прежде всего, наличия данных. В качестве источника данных будем использовать реестр обязательств банка перед вкладчиками (далее – реестр), формируемый ликвидируемым банком и передаваемый Государственной корпорации «Агентство по страхованию вкладов» (далее – Агентство) для осуществления страховых выплат. Реестр содержит информацию о вкладчиках данного банка, а также о взаимных обязательствах между банком и вкладчиками. В частности, реестр содержит информацию о ФИО и дате рождения каждого вкладчика, количестве открытых счетов, остатках денежных средств на этих счетах. Данные о фамилии, имени, отчестве позволяют автоматически определить пол вкладчика в 99 % случаев посредством морфологических анализаторов и справочников имен, размещенных в открытом доступе. Именно эти четыре признака мы будем хранить в матрице X и использовать для построения математических моделей. Отметим, что представление категориального признака «Пол» в виде пары бинарных «Пол_female» и «Пол_male» значительного упростит дальнейшую обработку данных [1].
В качестве целевого признака, представляющего собой вектор y, очевидно, будем использовать информацию о сумме выплаченного (полученного вкладчиком) страхового возмещения, содержащуюся на момент написания статьи в учетных системах Агентства. Данный признак легко привести к бинарному, содержащему только значения (метки классов) True (или 1) и False (или 0), где True интерпретируется как факт обращения вкладчика за страховым возмещением, а False – как отсутствие такого обращения.
Наконец, разобьём матрицу X и вектор y на тренировочные Xtrain, ytrain (70 % данных) и тестовые Xtest, ytest (30 % данных) подмножества. На первом мы будем обучать математические модели, а с помощью второго – определять эффективность их работы.
Дерево решений. Первой моделью, значительным преимуществом которой является хорошая интерпретируемость результатов, выберем дерево решений (decision tree). Как предполагает термин «дерево решений», эту модель можно представить как разбиение данных на подмножества путем принятия решений, основываясь на постановке серии вопросов [2]. Более подробное описание принципов работы этой и последующих моделей выходит за рамки данной статьи, а потому здесь будет описан лишь подход при подборе параметров моделей, их итоговые значения, а также результаты работы моделей. Также необходимо отметить, что, если не оговорено иное, все модели импортировались из высоко оптимизированной библиотеки scikit-learn.
Для подбора параметров модели использовался оптимизационный поиск по сетке параметров (grid search) в совокупности с методом перекрестной проверки с откладыванием данных (holdout cross-validation). В качестве варьируемых параметров модели были выбраны максимальное количество итераций разбиений дерева решений на подмножества (max_depth), минимальное количество элементов в каждом из подмножеств (min_samples_leaf), а также критерий разбиения данных (criterion). Стоит отметить, что при подборе параметров модели здесь и далее использовалась метрика оценки качества roc_auc (receiver operator characteristic; area under the curve), вместо accuracy (отношение верно предсказанных меток класса к общему количеству предсказаний), используемая по умолчанию. Это связано с вероятностью неравномерного соотношения меток класса 1 и 0 в векторе целевого признака y, что делает использование стандартной метрики accuracy нецелесообразным. Что касается интерпретации результатов в метрике roc_auc – ограничимся утверждением, что абсолютной предсказательной точности модели соответствует значение roc_auc = 1 [3].
В результате лучшими параметрами модели оказались:
- criterion = ‘entropy’,
- max_depth = 7,
- min_samples_leaf = 167,
при roc_auc = 0.9340. Данные параметры интерпретируются следующим образом: критерием при выборе признака и его значения для разбиения является уменьшение суммарной энтропии (меры неоднородности) в получаемых подмножествах. При этом разбиения происходят до тех пор, пока каждый образец данных не поучаствует в 7 разбиениях или пока в подмножестве находится более 167 образцов.
При этом качество предсказаний на отложенных данных Xtest, ytest в разных метриках равно:
- accuracy = 0.8854,
- precision = 0.9256,
- recall = 0.7864,
- roc_auc = 0.9330,
где метрика precision – отношение верно предсказанных значений «1» к общему количеству предсказанных «1», а recall – отношение верно предсказанных значений «1» к действительному общему количеству значений «1». Иными словами, интерпретируя предсказательную способность модели, мы почти не ошибаемся, говоря, что вкладчик придёт за страховым возмещением, но ошибаемся чаще, утверждая, что он не обратится за деньгами.
Как утверждалось ранее, деревья решений предоставляют инструменты для интерпретации результатов. Так, можно установить, в какой степени тот или иной признак влияет на факт обращения вкладчика за страховым возмещением: ожидаемо, факт обращения за страховым возмещением на 97.42 % обусловлен суммами, находящимися на счетах вкладчика в ликвидируемом банке. Из второстепенных признаков наибольшее влияние оказывает возраст вкладчика (1.2 %).
Наконец, приведем упрощённую версию закономерностей, выявленных моделью.
- Вкладчики, на счетах которых больше 6640 руб., как правило, обращаются за страховым возмещением. Исключение составляют мужчины старше 59 лет, на счетах которых находится от 6640 до 9303 руб.
- Вкладчики, на счетах которых меньше 2044 руб., как правило, не обращаются за страховым возмещением. Исключение составляют женщины от 29 до 78 лет, на счетах которых находится от 1799 до 2044 руб.
- Вероятность обращения за страховым возмещением вкладчиков, на счетах которых от 2044 до 6640 руб., равна примерно 50 % и в основном зависит от пола вкладчика: женщины, как правило, обращаются за деньгами, тогда как мужчины не всегда обращаются.
Метод ближайших соседей (k-nearest neighbor classifier, KNN) классифицирует каждый образец данных (в нашем случае – вкладчика) на основе классов нескольких наиболее похожих образцов. В качестве варьируемых параметров модели выберем количество ближайших образцов (n_ neighbors), коэффициент (p), использующийся при расчете расстояния (вычисления схожести) между образцами, а также способ взвешивания образцов в рамках каждой группы соседей.
В результате лучшими параметрами модели оказались:
- weights = ‘uniform’,
- n_ neighbors = 46,
- p = 1,
при roc_auc = 0.9258. То есть для оптимального предсказания факта обращения вкладчика за возмещением необходимо взять 46 наиболее «похожих» на него вкладчиков. «Похожесть» вычисляются с помощью так называемого манхэттенского расстояния, при этом степень «похожести» роли не играет.
Качество предсказаний на отложенных данных Xtest, ytest в различных метриках равно:
- accuracy = 0.8772,
- precision = 0.9350,
- recall = 0.7566,
- roc_auc = 0.9262.
Результаты этого и последующих методов менее интерпретируемы, нежели результаты дерева решений, а потому при оценке работы модели остаётся довольствоваться исключительно степенью достоверности предсказаний.
Логистическая регрессия базируется на итеративном вычислении вероятности принадлежности образца к тому или иному классу, а затем вычислении по всем образцам функции стоимости – «штрафа» за недостоверные предсказания. В качестве варьируемых параметров будем использовать способ и коэффициент регуляризации при вычислении значения функции стоимости.
Наиболее оптимальной оказалась L2-регуляризация (квадратичная) с коэффициентом 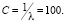
Качество предсказаний на отложенных данных Xtest, ytest в различных метриках равно:
- accuracy = 0.8549,
- precision = 0.9794,
- recall = 0.6641,
- roc_auc = 0.9013.
Случайный лес интуитивно может рассматриваться как ансамбль деревьев решений. В основе ансамблевого обучения лежит идея объединения слабых учеников для создания более устойчивой модели, т.е. сильного ученика с более хорошей ошибкой обобщения и меньшей восприимчивостью к переобучению [4].
Для оптимизации вычислительного процесса подберем наилучшие значения параметров max_depth и min_samples_leaf для ансамбля из 10 деревьев. После подбора таких параметров (max_depth = 9, min_samples_leaf = 31 при roc_auc = 0.9348) создадим итоговый классификатор, состоящий из 500 деревьев решений.
Качество предсказаний на отложенных данных Xtest, ytest в различных метриках равно:
- accuracy = 0.8850,
- precision = 0.9188,
- recall = 0.7929,
- roc_auc = 0.9352.
Бэггинг и Адаптивный бустинг (bagging, bootstrap aggregating и adaptive boosting) – также ансамблевые методы, в основу которых мы также заложим «слабых учеников» – неограниченное и ограниченное (равное единице) по параметру max_depth деревья решений, соответственно. Число деревьев в каждом ансамбле примем равным 500. Необходимость подбора оптимальных параметров модели в данном случае отсутствует.
В результате на тестовом наборе данных получены значения roc_auc = 0.9168 для бэггинга и roc_auc = 0.9338 для адаптивного бустинга.
Мажоритарное голосование (majority voting) – последняя рассматриваемая нами модель, также относящаяся к моделям ансамблевого обучения, то есть основывающаяся на работе нескольких классификаторов. Мажоритарное голосование просто означает, что мы отбираем метку класса, идентифицированную большинством классификаторов, т.е. получившую более 50 % голосов [5]. В качестве голосующих классификаторов выберем все рассмотренные выше модели. Отметим, что реализация данной модели, в отличие от всех предыдущих, не была импортирована из библиотеки scikit-learn.
В результате на тестовом наборе данных значение roc_auc для мажоритарного голосования составило 0.9325.
Результаты исследования и их обсуждение
Объединив результаты работы на отложенных (тестовых) данных всех рассмотренных моделей, можно утверждать, что в рамках рассматриваемой задачи большинство моделей показали себя в равной степени хорошо. Особо можно выделить результаты моделей на основе случайного леса, дерева решений и адаптивного бустинга. Наименьшие оценки заслужила модель на основе логистической регрессии.
Предполагается, что полученные результаты для всех моделей можно улучшить, например с помощью сжатия данных путем снижения размерности. Также очевидно, что добавление новых признаков (например, регион, в котором работает банк и/или проживает вкладчик) положительно отразится на прогностической способности моделей, особенно когда речь идёт об их использовании применительно к непохожим друг на друга банкам, в каждом из которых может наблюдаться собственная специфика.
Тестирование на других банках. Для проверки результатов работы моделей используем данные реестра другого банка, лицензия которого была отозвана в начале 2019 г. Вкладчиками данного банка являлись около 11,2 тыс. граждан, на счетах которых было размещено около 3 млрд рублей. С помощью модели, построенной на основе случайного леса, спрогнозируем обращения вкладчиков данного банка за страховым возмещением, а затем соотнесем с соответствующими известными данными. В результате получаем следующие оценки в различных метриках:
- accuracy = 0.9316,
- precision = 0.9422,
- recall = 0.9248,
– наблюдаем даже лучшие показатели, чем на обучающей выборке, что, вероятно, объясняется спецификой данных тестируемого банка.
Заключение
Построены несколько моделей машинного обучения, лучшие из которых способны прогнозировать обращения вкладчиков банка за страховым возмещением с точностью около 90 %. Факты обращения почти полностью обусловлены суммами на счетах вкладчиков. Кроме того, можно сделать вывод, что для вкладчиков исследуемого банка суммы свыше 6 тыс. рублей являются достаточно значительными, а суммы меньше 2 тыс. рублей, в свою очередь, недостаточно значительными для подачи заявления на выплату страхового возмещения.
Полученные модели могут служить:
- для прогнозирования нагрузки на офисы банков-агентов, выплачивающих страховое возмещение;
- для прогнозирования невостребованной суммы страхового возмещения по страховому случаю.
Библиографическая ссылка
Горелик А.В., Григорьев А.П. ПРОГНОЗИРОВАНИЕ ОБРАЩЕНИЙ ВКЛАДЧИКОВ БАНКА ЗА СТРАХОВЫМ ВОЗМЕЩЕНИЕМ С ПОМОЩЬЮ МЕТОДОВ МАШИННОГО ОБУЧЕНИЯ // Современные наукоемкие технологии. 2020. № 11-1. С. 21-24;URL: https://top-technologies.ru/ru/article/view?id=38332 (дата обращения: 27.12.2025).
DOI: https://doi.org/10.17513/snt.38332



