Современный уровень развития производства, технологических процессов изготовления различных изделий и актуальная на сегодня стадия технического прогресса должны быть обеспечены специалистами инженерного профиля, свободно владеющими современными компьютерными технологиями и обладающими технической эрудицией, которая включает графическую составляющую, то есть знания и умения разработки конструкторской документации, обладание пространственным мышлением и навыками построения проекций пространственных моделей.
Следовательно, по-прежнему актуальными остаются дисциплины графического цикла: начертательная геометрия, инженерная графика и компьютерная графика, формирующие вышеперечисленные компетенции. Учебный процесс при изучении теории начертательной геометрии – базовой графической дисциплины, формирующей основы изложения пространственных представлений и образов на плоском чертеже (эпюре), строится, как правило, классическим способом. Теоретические лекционные занятия, практические занятия с решением задач графическими методами, при помощи дополнительных построений. Повышение наглядности классических лекций достигается с применением мультимедийных презентаций [1]. Практические занятия проводятся с использованием рабочих тетрадей, позволяющих студенту не перечерчивать условие задачи, а сразу выполнять построения, суть которых составляет решение задачи. При этом остается невостребованным процесс моделирования пространственных объектов при помощи современных компьютерных технологий [2]. Данное виртуальное твердотельное моделирование значительно повышает наглядность учебного процесса при изучении графических дисциплин.
Цель исследования: разработка методики выполнения практической работы по теме пересечения поверхностей.
Материалы и методы исследования
Применение твердотельного моделирования возможно при изучении темы «Пересечение поверхностей» в начертательной геометрии. Данная тема изучается в финальной части курса и может быть максимально визуализирована с применением компьютерных технологий. Рассмотрим возможности визуализации на конкретном примере решения задачи по пересечению поверхностей, но для начала классифицируем пересечения поверхностей по способам их построения и форме получающихся линий пересечения. Это позволит представить возможности комбинирования компьютерных технологий с классическими способами построения линии пересечения поверхностей.
По нашему мнению, методика выполнения практической работы по теме «Пересечение поверхностей» должна включать в себя несколько следующих этапов: построение модели пересекающихся поверхностей, визуальный этап просмотра построенной модели, построение ассоциативного чертежа, дооформление его по правилам построения линии пересечения поверхностей, определяющего и корректирующего общие точки линии пересечения с использованием инструментария геометрических построений.
Прежде всего, следует пояснить понятие «поверхность». В начертательной геометрии поверхность определяют как последовательные положения некой движущейся линии кинематическим способом при перемещении образующей линии по направляющей линии. По форме образующей линии поверхности подразделяются на линейчатые (образуются при перемещении прямой линии) и нелинейчатые поверхности (образуются кривыми). Линейчатые поверхности в свою очередь делятся на развертываемые и неразвертываемые поверхности. Обзоры поверхностей представлены в учебниках начертательной геометрии [3]. Отдельно в классической литературе по данной дисциплине рассматриваются многогранники, поверхности вращения и винтовые линии. Изучение кривых поверхностей расширяет пространственное видение окружающего мира у обучаемого. Кривые поверхности существуют в природе, в быту, в строениях. Возможности компьютерных технологий позволяют выполнить построение кривых поверхностей в виртуальном пространстве, и это необходимо использовать при изучении классических графических дисциплин. При этом нахождение линии пересечения поверхностей остается актуальной графической задачей, позволяющей выполнить построение линий перехода различных поверхностей любой детали на изображениях чертежа.
Нахождение линии пересечения поверхностей выполняется при помощи вспомогательных секущих поверхностей. Этими поверхностями могут быть плоскости и некоторые кривые (например, сферы). Для определения общих точек поверхностей используют: плоскости общего и частного положения, кривые поверхности, линейчатые образующие поверхностей и ребра многогранников.
При использовании вспомогательных секущих плоскостей их располагают либо параллельно плоскостям проекций, либо частным способом, дающим в пересечении с заданными поверхностями прямые линии, например, при пересечении линейчатых конусов и (или) цилиндров. Использование плоскостей, параллельных плоскостям проекций, возможно в случае, когда в пересечении с заданными поверхностями получаем прямые или окружности.
Использование вспомогательных сфер ограничено следующими положениями: обе пересекающие поверхности относятся к поверхностям вращения, имеют общую плоскость симметрии и их оси вращения пересекаются. Это определяет применение концентрических сфер с общим центром вращения. Определившись со способом построения линии пересечения кривых поверхностей, выделим их возможные формы.
Форма линии пересечения зависит от пересекающихся поверхностей:
а) если пересекаются две многогранные поверхности, то форма линии пересечения – ломаная прямая;
б) если пересекаются многогранная и кривая поверхности, то форма линии пересечения – плавная кривая с точками излома на ребрах многогранника;
в) если пересекаются две кривые поверхности, то форма линии пересечения – плавная кривая.
Рассмотрим решение задачи на построение линии пересечения поверхностей способом сечений вспомогательными секущими плоскостями.
Построение линии пересечения представлено на рис. 1.
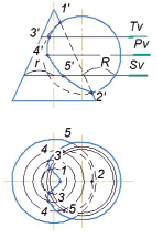
Рис. 1. Пересечение конуса и сферы
Решение:
1. Устанавливаем, что форма линии пересечения заданных поверхностей конуса и сферы – плавная кривая.
2. Так как нет проецирующей поверхности, то линия пересечения строится на обеих плоскостях.
3. Определяем характерные точки. Это точки 1 и 2, лежащие на пересечении контурных образующих.
4. Для нахождения точки 3 используем вспомогательную горизонтальную плоскость Тv:
- строим сечение конуса и сферы плоскостью Tv;
- в пересечении двух сечений находим горизонтальные проекции точек 3, принадлежащих одновременно обеим поверхностям, а значит, и линии пересечения;
-фронтальную проекцию точки 3 находим в проекционной связи на следе плоскости Tv.
5. Для нахождения точки 4 используем вспомогательную горизонтальную плоскость Pv.
6. Для нахождения точки 5 используем вспомогательную горизонтальную плоскость Sv.
7. Проекции точек 1–5 соединяем плавной кривой.
8. Определяем видимость линии пересечения и видимость поверхностей геометрических тел.
Точка 4 – точка изменения видимости (Т.И.В.).
Для наглядности представим способ построения модели при помощи аппарата трехмерного моделирования в программе Компас V17 [4]. Модель с деревом построения представлена на рис. 2.
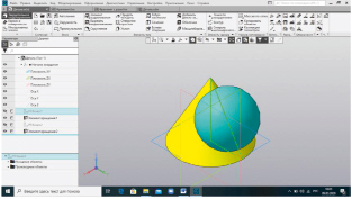
Рис. 2. Построение модели пересекающихся поверхностей
Последовательность построения следующая:
1. Выбираем плоскость ZY.
2. Выполняем эскиз, состоящий из наклонной образующей конуса и штрихпунктирной оси, совпадающей с осью Z.
3. Выполняем элемент вращения по построенному эскизу.
4. Выбираем плоскость ZY.
5. Выполняем эскиз, состоящий из дуги и осевой линии, выполненной штрихпунктирной линией.
6. Выполняем элемент вращения по заданному эскизу.
Результат – трехмерная модель, представленная на рис. 2. Выполним чертеж построенной модели. Используем панель Виды и команду Вид с модели. Ориентация: вид спереди и вид сверху. Получаем изображения, представленные на рис. 3.
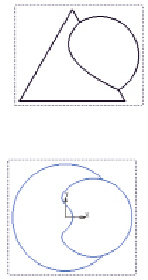
Рис. 3. Изображение пересечения поверхности конуса и сферы в двух проекциях
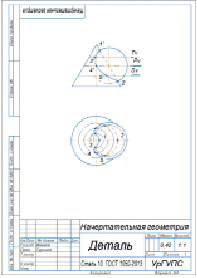
Рис. 4. Ассоциативный чертеж пересекающихся поверхностей
Изображение на рис. 3 представляет очерковые линии конуса и сферы и их линию пересечения – на фронтальную (вид спереди) и горизонтальную проекцию (вид сверху). Это изображение наглядно показывает кривую линию, по которой пересекаются заданные поверхности. Недостатком этого изображения является отсутствие атрибутов оформления его в соответствии с принятыми стандартами: отсутствие осевых и центровых линий. Чтобы устранить этот недостаток и привести данное изображение в соответствие со стандартами по оформлению чертежей, предлагаем внести в него дополнительные построения: осевые линии, задать секущие плоскости, определить несколько вспомогательных сечений, найти общие точки поверхностей и особенно ТИВ. Результат приведен на рис. 4.
Таким образом, задания по построению линии пересечения поверхностей, по нашему мнению, следует выполнять при помощи инструментария трехмерного моделирования в следующей последовательности:
Построение моделей заданных поверхностей с использованием Панели команд «Элементы тел». Поверхности вращения правильнее моделировать при помощи команды «Элемент вращения», эскизом которой должна быть образующая линии поверхности вращения, а ось вращения может быть задана в эскизе штрихпунктирной линией либо выбрана из осей проекции, имеющихся по умолчанию. При построении многогранников рационально использовать команды панели «Элементы тела», такие как «Элемент выдавливание», «Элемент по сечениям», «Уклон».
Следующий этап – просмотр выполненного элемента. Обзор пересекающихся поверхностей, формирующий пространственное представление о форме линии пересечения. При этом удобно использовать команды «Панели быстрого доступа», позволяющие настроить изображение: увеличить или уменьшить, переменить ориентацию, сделать изображение полутоновым или каркасным.
Построение основных видов пересекающихся поверхностей при помощи команд панели «Виды». Для этого создаем чертеж. Настраиваем формат. Используем команду «Стандартные виды с модели» либо «Вид» с модели. Важно в настройках будущих видов выбрать опцию «Передавать невидимые линии» и поставить галочку «Показывать невидимые линии». Создаем изображения чертежа, связанные с моделью пересекающихся поверхностей. Результат представлен на рис. 3.
При помощи команд панели «Геометрия», «Правка», «Обозначения» производим оформление чертежа: проводим осевые линии, а также выполняем построения общих точек на модели:
1. Определяем характерные точки. Это точки 1 и 2, лежащие на пересечении контурных образующих (для построений используем команды «Надпись», «Окружность», «Штриховка»).
2. Для нахождения точки 3 используем вспомогательную горизонтальную плоскость Тv:
– строим сечение конуса и сферы плоскостью Tv;
– в пересечении двух сечений находим горизонтальные проекции точек 3, принадлежащих одновременно обеим поверхностям, а значит и линии пересечения (используем также команды «Надпись», «Окружность», «Штриховка», «Отрезок», «Вспомогательная прямая»);
- фронтальную проекцию точки 3 находим в проекционной связи на следе плоскости Tv.
3. Для нахождения точки 4 используем вспомогательную горизонтальную плоскость Pv.
4. Для нахождения точки 5 используем вспомогательную горизонтальную плоскость Sv.
5. Определяем видимость линии пересечения и видимость поверхностей геометрических тел.
Точка 4 – точка изменения видимости (Т.И.В.) (при выполнении построений п 3–5 используем также команды «Надпись», «Окружность», «Штриховка», «Отрезок», «Вспомогательная прямая»). Результат представлен на рис. 4.
Результаты исследования и их обсуждение
В результате получаем построенное по правилам оформления чертежа изображение линии пересечения заданных поверхностей.
Так мы получаем разработанную с использованием возможностей компьютерных технологий практическую работу по начертательной геометрии, методику выполнения которой описали в [5].
Остановимся подробнее на преимуществах данной методики. Рассмотренная нами методика выполнения практической работы по начертательной геометрии совмещает в себе два образовательных направления графической подготовки:
а) изучение способов построения линии пересечения поверхностей;
б) изучение возможностей компьютерных программ, предназначенных для разработки чертежной документации, по виртуальным моделям.
Первое направление формирует у обучаемого навыки пространственного представления предметов по двухмерному изображению. И, напротив, обучает выполнению двухмерных изображений объемных конструкций на чертеже методом проекций [6].
Второе позволяет освоить удобный инструментарий для выполнения виртуальных изображений, оформленных с учетом требований Единой системы конструкторской документации.
Таким образом, первое преимущество состоит в совмещенной системе обучения двум востребованным в современной ситуации графическим дисциплинам: начертательной геометрии и компьютерной графике.
Другим преимуществом, с нашей точки зрения, является использование возможностей компьютерных технологий для усиления наглядности абстрактно-теоретической дисциплины. Построение модели пересекающих поверхностей – это виртуальная презентация пространственных линий пересечений поверхностей, доступная любому обучаемому.
Наличие чертежа, связанного с виртуальной моделью, позволяет выполнить точные построения точек линии пересечения с использованием инструментов панели «Геометрия». Построение вспомогательных точек методом плоскостей проекций в данном случае является критерием правильности создания заданных поверхностей. Это позволяет провести взаимную апробацию двух способов построения линии пересечения поверхностей.
Заключение
Рассмотрев преимущества данной методики решения задач, можно сделать вывод о том, что возможны различные способы решения классических графических задач с применением информационных технологий и многие их них описаны в педагогической литературе. Данное направление поисковой педагогической деятельности развивается с совершенствованием компьютерных технологий и способствует прогрессивным изменениям в обучении графическим дисциплинам.
Библиографическая ссылка
Вяткина С.Г., Туркина Л.В. РЕШЕНИЕ ЗАДАЧ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ С ПРИМЕНЕНИЕМ ТРЕХМЕРНОГО МОДЕЛИРОВАНИЯ В СИСТЕМЕ КОМПАС-3D V17 // Современные наукоемкие технологии. 2020. № 4-2. С. 277-282;URL: https://top-technologies.ru/ru/article/view?id=38010 (дата обращения: 01.07.2025).
DOI: https://doi.org/10.17513/snt.38010



