На сети железных дорог ОАО «РЖД» в эксплуатации находится более 120 тыс. стрелочных электроприводов (СЭ) различных типов. По большей части это устаревшие СЭ типа СП-6М и СП-6, которые составляют приблизительно 68 % и 19 % соответственно от общего числа. По данным ОАО «РЖД» за 2018 г. именно на СЭ вышеупомянутых типов приходится наибольшее число отказов, четверть из которых носят деградационный характер. СЭ являются дорогостоящими устройствами железнодорожной автоматики с продолжительным назначенным сроком службы. По истечении назначенного срока службы СЭ, как и другая аппаратура, должен подлежать списанию и утилизации, однако часто имеет место продление срока эксплуатации. Сложившаяся практика обусловлена дефицитом ресурсов компании ОАО «РЖД», который привел к невозможности реализации регламентного метода технического обслуживания. В частности, оказалось невозможным выполнять в полном объеме и в установленные сроки все необходимые работы по техническому обслуживанию и ремонту, а также проводить массовую замену аппаратуры, выработавшей назначенный срок службы.
В связи с этим в настоящее время компания меняет концепцию технической эксплуатации инфраструктуры в сторону рационализации расходов. На протяжении ряда лет внедряется методология управления ресурсами, рисками и анализа надежности, или УРРАН [1], которая базируется на разработанной для европейских железных дорог методологии RAMS [2]. В основе подхода, воплощаемого в методологии УРРАН применительно к инфраструктуре, лежит адресное распределение ресурсов по фактической потребности с одновременной минимизацией стоимости жизненного цикла аппаратуры.
Потребность в ресурсах определяется на основе диагностики состояния аппаратуры. В связи с необходимостью принятия решений по реализации различных мероприятий на основе фактического состояния аппаратуры и вышеуказанными проблемами технической эксплуатации непрерывная техническая диагностика и периодические осмотры приобретают особую важность. В настоящее время в компании применяется большое количество систем технической диагностики, а также иных информационных систем, в которых регистрируют различные данные о функционировании аппаратуры. Однако используются эти данные не в полной мере, так как они локализуются в своих информационных системах, представляются в разных видах и прирастают высокими темпами. В связи с этим особый интерес специалистами компании проявляется в направлении предиктивной аналитики [3]. В полной мере это относится к СЭ. Их состояние часто контролируется той или иной системой технической диагностики и мониторинга (СТДМ), выявляющей помимо прочего предотказные состояния. Если в СЭ происходят отказы, то они фиксируются в системах КАСАНТ и АСУ-Ш-2; результаты комиссионных осмотров в виде отступлений от норм содержания фиксируют в системе ЕК АСУИ. Эти сведения, представляющие собой преимущественно статистические данные, в совокупности позволят определять фактическое состояние каждого СЭ и динамику его изменения, а следовательно, с их использованием можно попытаться дать индивидуальную оценку остаточного ресурса до достижения предельного состояния, что с учетом вышесказанного актуально для реализации методологии УРРАН. Однако различные данные по-разному характеризуют состояние СЭ.
В настоящей статье предлагается метод индивидуальной точечной оценки остаточного ресурса СЭ, впервые позволяющий обобщить статистические данные из различных источников.
Метод оценки остаточного ресурса СЭ базируется на взвешенном методе наименьших квадратов (взвешенном МНК), где веса определяются с учетом специфики хранимых в разных информационных системах статистических данных.
Следует отметить, что ранее предпринимались попытки оценки остаточного ресурса [4]. Вместе с тем ранее применялся классический МНК, приводивший к существенным отклонениям оценок остаточного ресурса при наличии «промахов». Кроме того, метод применялся целиком для систем железнодорожной автоматики и телемеханики, а не для аппаратуры.
Цель исследования: разработка метода для получения уточненных точечных оценок остаточного ресурса СЭ.
Основными задачами являются:
– разработка математической модели, обобщающей статистические данные из разных информационных систем;
– формирование регрессионного тренда взвешенным МНК для оценки динамики состояния СЭ;
– формирование критерия остаточного ресурса СЭ.
Метод оценки остаточного ресурса стрелочных электроприводов
Исходные данные представляют собой моменты наступления различных событий с СЭ: отказов, предотказных состояний и отступлений от норм содержания СЭ. События происходят формально в случайные моменты времени. Формат данных единообразен для всех категорий событий, поэтому для удобства все перечисленные случайные события будем называть общим термином «событие».
В качестве ключевого показателя при оценке остаточного ресурса предлагается использовать частоту событий, вычисляемую на основе данных о моментах их регистрации. В этом случае исходные данные о различных событиях для оценки остаточного ресурса конкретного типа СЭ по частоте событий можно представить кортежем вида
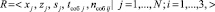 (1)
(1)
где xj – инвентарный номер СЭ;
zj – двоичный оператор, учитывающий год эксплуатации (1 – последний год до прекращения эксплуатации, 0 – не последний год до прекращения эксплуатации);
sj – условный номер года начала отсчета при формировании статистической совокупности данных о событиях (используется сквозная нумерация от 1 (год начала наблюдения) до m (год окончания наблюдения);
tсоб j – время регистрации события с начала наблюдения, выраженное в часах;
nсоб ij – количество зарегистрированных событий в момент времени tсоб j;
i – уровень критичности (приоритета) события;
N – мощность кортежа событий.
Моменты наступления событий tсоб следует упорядочить в порядке регистрации во времени от более ранних событий к более поздним по индексу j.
Уровень критичности для событий вида «отступления от норм содержания» и «предотказные состояния» определяют в соответствии с утвержденными в хозяйстве автоматики и телемеханики классификаторами.
На основе кортежа (1) формируют кортеж для определения значения частоты событий, соответствующей предельному состоянию СЭ:
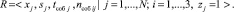 (2)
(2)
Уровень приоритета (критичности) событий предлагается учитывать соотношением
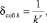 (3)
(3)
где r – коэффициент приоритета (критичности) событий (натуральное число, рекомендуемое значение r = 2).
Для каждого элемента кортежей (1) и (2) выполняют расчет результирующей частоты событий по формуле
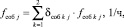 (4)
(4)
а также интервала между событиями:
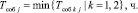 (5)
(5)
После обработки с помощью формул (3)–(5) кортежа (1) формируют кортеж, используемый для построения регрессионного тренда, описывающего динамику ключевого показателя различных СЭ определенного типа во времени:
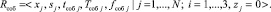 (6)
(6)
Результаты расчета реализаций частоты событий, выполненных на основе кортежа (2) и характеризующих предельное состояние СЭ, описывают кортежем вида
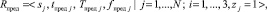 (7)
(7)
где tпред j – время события с начала наблюдения (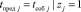 );
);
Tпред j – интервал времени между событиями (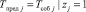 );
);
fпред j – результирующая частота событий (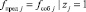 ).
).
Таким образом, формируется единая совокупность реализаций частоты различных событий с СЭ.
Далее на основе данных, представленных в виде кортежа (6), для каждого xj СЭ выполним построение линейного тренда.
Оценку текущего технического состояния СЭ и прогноз динамики его изменения предлагается осуществлять путем построения регрессионного тренда [5]. Для этого по указанным ранее причинам используем взвешенный метод наименьших квадратов, где вес каждой точки данных определяется давностью точки во времени и ее локальным отклонением от общей совокупности. Последнее является важным, так как в регистрируемых информационными системами статистических данных иногда встречаются значительные «промахи» (выбросы), существенно ухудшающие точность построения тренда обычным методом наименьших квадратов.
Общее уравнение зависимости фактического значения частоты событий, произошедших с конкретным СЭ, от времени имеет вид
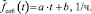 (8)
(8)
Коэффициенты a и b – параметры тренда.
Для расчета коэффициентов используем формулы взвешенного метода наименьших квадратов вида
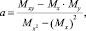 (9)
(9)
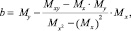 (10)
(10)
где 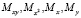 – коэффициенты, определяемые на основе статистических данных из кортежа (6) по формулам
– коэффициенты, определяемые на основе статистических данных из кортежа (6) по формулам
 (11)
(11)
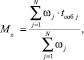 (12)
(12)
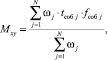 (13)
(13)
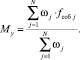 (14)
(14)
Расчет параметров тренда осуществим в два этапа:
– предварительная грубая оценка;
– окончательная уточненная оценка.
Для грубой оценки параметров тренда уравнение (8) представим в виде
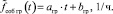 (15)
(15)
При данной оценке в выражениях (11)–(14) установим значения коэффициентов ωj равными единице: 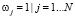 .
.
Для окончательной уточненной оценки (по формуле (8)) параметров тренда 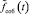 выполним расчет весовых коэффициентов ωj по формуле:
выполним расчет весовых коэффициентов ωj по формуле:
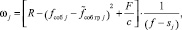 (16)
(16)
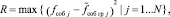 (17)
(17)
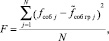 (18)
(18)
где f – количество лет, входящих в интервал наблюдения;
c – коэффициент, подбираемый опытным путем;
N – объем статистической совокупности событий в таблице.
Допустимое значение частоты событий, характеризующее наступление предельного состояния СЭ fпред, вычислим по элементам кортежа (7), удовлетворяющим условию sj = 1:
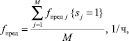 (19)
(19)
где М – объем статической совокупности с sj = 1 в кортеже (7).
Критерий предельного состояния имеет вид
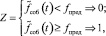 (20)
(20)
где при Z = 0 – состояние СЭ не является предельным, при Z = 1 – состояние СЭ является предельным.
Остаточный ресурс будем рассматривать как интервал времени, по истечении которого СЭ из текущего состояния перейдет в предельное, если предельное состояние на настоящий момент времени еще не достигнуто.
Для оценки остаточного ресурса СЭ, прежде всего, определим момент на шкале времени тренда, от которого потребуется проводить оценку остаточного ресурса [4]:
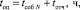 (21)
(21)
где tсоб N – момент события, соотнесенный с последним элементом кортежа (6);
tотч – интервал времени от момента фиксации последнего события tсоб N до момента времени, когда выполняется расчет остаточного ресурса, ч.
Оценку остаточного ресурса СЭ в часах выполним по формуле
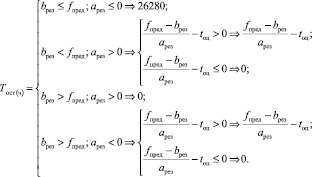 (22)
(22)
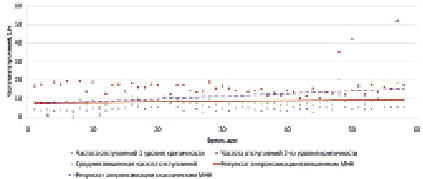
Регрессионные тренды, построенные классическим и взвешенным МНК
Так как мероприятия по замене и капитальному ремонту оборудования в компании планируют на следующий по отношению к текущему календарный год, то остаточный ресурс выразим количеством календарных лет до достижения предельного состояния:
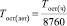 , лет. (23)
, лет. (23)
С целью оценки эффекта от применения взвешенного МНК по схеме (16), (17) была выполнена апробация метода на моделированных данных.
Апробация метода
В качестве моделированных данных использовались нормально распределенные реализации отступлений от норм содержания и предотказных состояний с уровнями критичности 1 и 2. Для событий 1ого уровня критичности параметры распределения были следующие: математическое ожидание – 5 1/ч, стандартное отклонение – 1 1/ч; для событий 2-го уровня критичности: математическое ожидание – 6 1/ч, стандартное отклонение – 3 1/ч. Дополнительно были подсеяны «промахи» для неблагоприятного случая.
На рисунке представлен результат построения регрессионного тренда различными модификациями метода наименьших квадратов на основе моделированных данных для наихудшего случая.
Для количественной оценки качества обоих трендов вычислялось остаточное стандартное отклонение. Результат представлен в таблице.
Сравнительная характеристика трендов, построенных классическим и взвешенным МНК
|
Взвешенный МНК |
Классический МНК |
|
|
Без удаления промахов |
2,1 |
3,0 |
|
После удаления промахов |
0,9 |
2,3 |
Как видно из рисунка, регрессионный тренд, построенный взвешенным методом наименьших квадратов на основе взвешенных значений результирующей частоты событий, существенно менее чувствителен к выбросам в статистических данных и учитывает специфику данных об отказах, отступлениях от норм содержания и предотказных состояниях СЭ, когда интервалы между отдельными событиями могут быть очень малы.
Заключение
Разработанный метод позволяет получать более точные оценки остаточного ресурса, по сравнению с классическим МНК. В то же время его реализация требует больших вычислительных ресурсов, поэтому целесообразность и объем применения предложенного метода должны определяться техническими возможностями информационных систем. В дальнейшем по мере их развития будет представлять интерес интервальная оценка остаточного ресурса.
Работа выполнена при финансовой поддержке РФФИ (номер гранта: 17-20-03072, код: офи-м-РЖД).
Библиографическая ссылка
Горелик А.В., Дорохов В.С., Орлов А.В., Смагин Ю.С. СТАТИСТИЧЕСКАЯ ОЦЕНКА РЕСУРСА СТРЕЛОЧНЫХ ЭЛЕКТРОПРИВОДОВ // Современные наукоемкие технологии. 2019. № 9. С. 58-63;URL: https://top-technologies.ru/ru/article/view?id=37666 (дата обращения: 04.07.2025).



