Высокопроизводительные вычисления в последние годы приобретают все большую популярность практически во всех сферах жизни, позволяя открывать новые горизонты в области применения информационных технологий в научной деятельности.
Общая тенденция в области параллельных вычислений состоит в адаптации существующих алгоритмов, разработанных для гомогенных параллельных систем, к гетерогенным системам. Однако допущения, принятые для однородных систем, не всегда применимы к неоднородным системам.
Параллельное умножение матриц является одной из самых распространенных задач в самых различных областях научных вычислений, таких как астрономия, метеорология, физика и химия. В то время как вопрос оптимального распределения матриц между гомогенными вычислительными узлами достаточно широко изучен, оптимальные решения для гетерогенных систем, которые на данный момент получают все более широкое распространение, является до сих пор открытым.
Разбиение данных определяет способы распределения частей матриц среди доступных вычислительных элементов при выполнении операций линейной алгебры. Оно производится с целью сокращения времени выполнения вычислений.
Прямоугольные формы разбиения данных рассматривались в работах [1–3]. В работах [4, 5] было доказано, что при определенных соотношениях вычислительных мощностей процессоров оптимальными могут являться и непрямоугольные формы разбиения элементов матриц. Однако при этом не учитывалась разница пропускных способностей сетей передачи данных между вычислительными элементами.
Цель исследования: определить, являются ли справедливыми выводы об оптимальности форм разбиения данных, полученные в случае использования гетерогенных систем с равными пропускными способностями, для систем с различной пропускной способностью между процессорами.
Материалы и методы исследования
Для моделирования умножения матриц в данной работе используется абстрактная модель процессора, рассмотренная в работах [6, 7]. В работе [4] было доказано, что понятие абстрактного процессора, которое фокусируется главным образом на объеме коммуникаций и объеме вычислений, точно прогнозирует экспериментальную производительность множества процессоров и даже целых кластеров для матричных вычислений.
Для эффективного моделирования умножения матриц на трех абстрактных гетерогенных процессорах было сделано несколько допущений:
– в работе использованы квадратные исходные матрицы A, B и результирующая матрица С размером N×N элементов;
– элементы матрицы разделены между абстрактными процессорами P, R и S, пропорционально их вычислительным мощностям, которые определены отношением Pr : Rr : Sr, где P является самым мощным процессором и Sr = 1. T = Pr + Rr + Sr;
– процессоры объединены полносвязной топологией, с пропускными способностями сети передачи β1 между процессорами P и S, β2 между процессорами P и R, β3 между процессорами S и R;
– в качестве форм-кандидатов рассмотрены формы Square Corner (SC), Rectangle Corner (RC), Square Rectangle (SR), Block Rectangle (BR), L-Rectangle (LR), Traditional 1D Rectangular (TR), выявленные Эшли ДеФлумьер в работе [5, с. 77] в результате применения техники перераспределения элементов матрицы между процессорами «Push» (рис. 1):
– для оценки коммуникационной трудоемкости рассматриваемых алгоритмов использована модель Хокни.
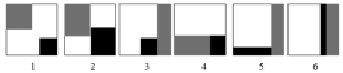
Рис. 1. Формы-кандидаты, определенные как потенциально оптимальные для трехпроцессорных систем: 1) Square Corner; 2) Rectangle Corner; 3) Square Rectangle; 4) Block Rectangle; 5) L-Rectangle; 6) Traditional 1D Rectangular
Определение оптимальной формы разбиения данных для алгоритмов последовательной коммуникации с барьером
Алгоритм последовательной коммуникации с барьером (Serial Communication with Barrier, SCB) – простой алгоритм матричного умножения, в котором все данные пересылаются процессорами последовательно, вычисления начинаются только после того, как все процессоры завершили передачу данных и выполняются параллельно (рис. 2).
Время выполнения алгоритма включает в себя время коммуникации между процессорами и время, необходимое на выполнение вычислений:
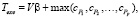(1)
где V – общее количество коммуникаций;
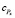– время, необходимое процессору X для вычисления назначенной ему части матрицы С.
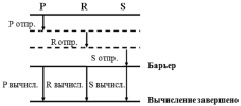
Рис. 2. Алгоритм последовательной коммуникации с барьером для процессоров P, R и S
Так как площадь матрицы и количество элементов, выделенных каждому процессору, пропорциональны его вычислительной мощности, параметр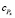 
будет одинаков для всех рассматриваемых форм кандидатов и, соответственно, может не учитываться при сравнении времени выполнения алгоритма.
Определим время коммуникации Tcomm для каждой рассматриваемой формы согласно формуле (1).
SC: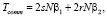 
SR: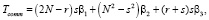 
BR: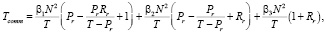 
LR: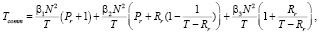 
TR: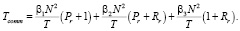 
Для формы Rectangle Corner оптимальный размер R и S будет являться комбинированной шириной N, что не может быть истиной исходя из классификации форм-кандидатов [5, с. 78]. В качестве альтернативы установим, что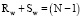 
. Тогда
RC: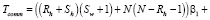 
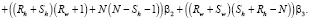
Для облегчения анализа полученной математической модели избавимся от коэффициента β3, получив отношения пропускных способностей между вычислительными элементами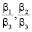 
. Таким образом, мы получаем четыре переменные.
Для выполнения теоретических расчетов было разработано программное обеспечение на языке программирования Java, позволяющее в текстовом виде или через web-интерфейс вводить исходные параметры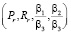 
и определять оптимальную форму разбиения данных (рис. 3).
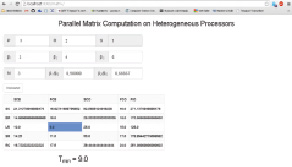
Рис. 3. Пример программных расчетов при значениях Pr = 3, Rr = 2,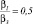 
, 
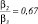
Исходя из проведенного анализа полученных данных были сделаны следующие выводы. Для алгоритма SCB оптимальными могут являться формы разбиения элементов матрицы BR, LR, SC, SR. Форма LR оптимальна при значении коэффициента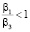 
и примерно равных мощностях процессоров P и R, значительно превышающих мощность процессора S. Форма SR может являться оптимальной в случаях малых значений коэффициентов 
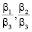и мощностях процессоров P и R, значительно превышающих мощность процессора S. Во всех остальных случаях оптимальными являются формы BR и SC.
Определение оптимальной формы разбиения данных для алгоритмов параллельной коммуникации с барьером
Алгоритм параллельной коммуникации с барьером (PCB) предполагает, что пересылка данных между процессорами осуществляется параллельно и только после того как коммуникация полностью завершена, процессоры приступают к параллельному выполнению вычислений (рис. 4).
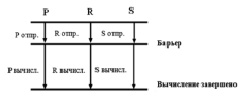
Рис. 4. Алгоритм параллельной коммуникации с барьером для процессоров P, R и S
Оценка времени выполнения алгоритма производится по формуле
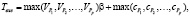(2)
где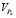 
– объем данных, который должен быть передан процессором X.
Аналогично алгоритму SCB параметр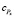 
может не учитываться в формулах, определение оптимальности форм будет произведено исходя из времени коммуникации Tcomm.
SC: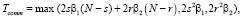 
SR: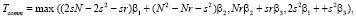 
BR: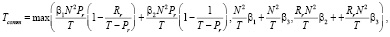 
LR: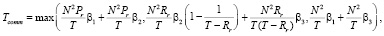 
TR: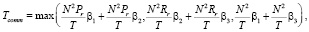 
RC: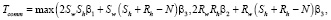 
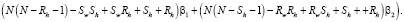
По результатам, полученным с помощью разработанного програмного обеспечения, были сделаны следующие выводы. Как и в случае использования алгоритма SCB, оптимальными могут являться только формы BR, LR, SC, SR. LR оптимальна только при значениях коэффициентов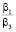 
= 0,1, 
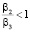и примерно равных мощностях процессоров P и R гораздо больших S. SR может являться оптимальной при 
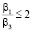и значениях мощностей процессоров P и R значительно превышающих мощность процессора S. В остальных случаях в зависимости от выбранных параметров оптимальными являются формы BR и SC.
Заключение
На основании полученных результатов можно сделать заключение, что, как и в случае трехпроцессорных систем с одинаковой пропускной способностью сетей, соединяющих вычислительные элементы, формы разбиения данных Rectangle Corner и Traditional 1D Rectangular не могут быть оптимальными ни при одном наборе параметров.
В отличие от результатов, полученных в работе [5, с. 85, 88], форма L-Rectangle может быть оптимальной при мощностях процессоров P и R, намного превышающих мощность процессора S и примерно равных друг другу в случае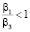 
для алгоритма SCB и 
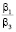= 0,1 для алгоритма PCB. Однако в данных случаях нет смысла в использовании маломощного процессора S, и задача может быть решена на двух процессорах.
Форма Square Rectangle является оптимальной при малых значениях коэффициентов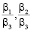 
и мощностях процессоров P и R, значительно превышающих мощность процессора S. При таких исходных данных задача также может быть решена с использованием двух мощных процессоров.
В остальных случаях оптимальными в случае использования обоих алгоритмов в зависимости от значений коэффициентов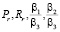 
являются формы Square Corner и Block Rectangle.
Результаты исследования показывают, что данные приближенные прямоугольные решения являются субоптимальными для множества гетерогенных соотношений вычислительных мощностей процессоров при использовании рассмотренных алгоритмов умножения матриц.
Библиографическая ссылка
Клюева Е.Г., Адамов А.А., Оспанова А.Е., Сницарь Л.Р., Кулбаева Л.Н. ИССЛЕДОВАНИЕ ОПТИМАЛЬНОЙ ФОРМЫ РАЗБИЕНИЯ ДАННЫХ ДЛЯ УМНОЖЕНИЯ МАТРИЦ НА ТРЕХ ГЕТЕРОГЕННЫХ ПРОЦЕССОРАХ С ПОЛНОСВЯЗНОЙ ТОПОЛОГИЕЙ И РАЗЛИЧНЫМИ ПРОПУСКНЫМИ СПОСОБНОСТЯМИ // Современные наукоемкие технологии. – 2019. – № 2. – С. 83-88;URL: https://top-technologies.ru/ru/article/view?id=37413 (дата обращения: 19.04.2024).