В настоящее время вопросам получения материалов с улучшенными свойствами [1–3], исследованиям процессов их деформирования и разрушения при различных видах нагружения [2–4] уделяется повышенное внимание. Одним из видов перспективных конструкционных материалов считаются металло-интерметаллидные слоистые композиционные материалы (МИСКМ) [5]. Из-за особенностей своей структуры МИСКМ обладают высокими удельными прочностными характеристиками и являются баллистически стойкими. МИСКМ представляют собой пример так называемых биоподобных материалов и имеют многослойную композицию из взаимно чередующихся слоев интерметаллида и слоев металла или сплава. На создание таких материалов ученых натолкнуло исследование структур природных биологических систем, например структуры раковины морского моллюска Haliotis rufescens (abalone, морское ушко) представляет собой твердые хрупкие слои CaCO3, склеенные пластичной граничной органической фазой. В случае композитов Ti-Al3Ti, триалюминид титана (Al3Ti), который обладает высокой твердостью и прочностью на сжатие при относительно низкой плотности, имитирует роль плиток CaCO3, а пластичные и трещиностойкие слои из титанового сплава (BT6), необходимые для остановки магистральных трещин и рассеивания энергии удара за счет пластической деформации, выступают в роли граничной связующей фазы.
Процессы динамического нагружения МИСКМ до сих пор мало исследованы. Им посвящено незначительное число как экспериментальных, так и теоретических работ. В экспериментальных исследованиях достаточно трудно регистрировать динамику высокоскоростного процесса. Анализ сохраненных после нагружения образцов не дает достоверной оценки механизмов разрушения. Численное моделирование, в рамках используемых математических моделей, позволяет исследовать динамику деформирования и разрушения нагружаемых тел [6].
В настоящее время численным методам исследования механического поведения сложных технических систем уделяется повышенное внимание. Очень часто для анализа используются коммерческие программные продукты, такие как MatLab [7, 8], ALGOR, САПР Solid Works (Cosmos Works), ANSYS [9]. Наиболее популярным численным методом, используемым для решения задач деформирования и разрушения материалов и элементов конструкций, является метод конечных элементов (МКЭ), который лежит в основе упомянутых выше программных пакетов. Вместе с тем актуальной остается разработка исследовательских программных комплексов на основе МКЭ [6, 10].
В данной работе методом численного моделирования исследуется процесс нагружения многослойной преграды Ti-Al3Ti при начальных скоростях удара 2000, 3000 и 5000 м/с. Такие скорости в экспериментах могут обеспечиваться с использованием легкогазовой установки. Цель работы – оценить влияние начальной скорости ударника на характер разрушения преграды, на ее прочностные характеристики и степень поврежденности после взаимодействия. Для численного моделирования динамических процессов используется исследовательский программный комплекс на основе МКЭ.
Материалы и методы исследования
В работе используется модель повреждаемой среды, характеризующаяся наличием в материале микроповреждений. В качестве параметра поврежденности материала применяется удельный объем микроповреждений Vf :
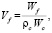 (1)
(1)
где Wf – объем, занимаемый микроповреждениями, рc – плотность неповрежденной части, Wc – объем, занимаемый неповрежденной частью среды.
Система основных уравнений состоит из уравнений неразрывности, движения и энергии, являющихся следствиями законов сохранения массы, импульса и энергии [11]. Уравнение состояния (УРС) строится по типу уравнения Ми-Грюнайзена, в котором предполагается наличие «холодной» и «тепловой» частей. УРС определяет давление в неповрежденном веществе во всем диапазоне условий нагружения как функцию удельного объёма и удельной внутренней энергии. Коэффициенты УРС определяются через константы ударной адиабаты Гюгонио. Для связывания компонент девиатора напряжений и компонент тензора скоростей деформаций используются определяющие соотношения, содержащие производную по Яуманну. Для описания пластического течения используется условие текучести Мизеса. В процессе вычислений рассматривается влияние температуры и поврежденности материала на модуль сдвига и динамический предел текучести [11].
Для слоев из титанового сплава применяется кинетическая модель разрушения активного типа [11], которая позволяет моделировать разрушение в металлах при растяжении. Для слоев из интерметаллида применяется модель разрушения хрупкого типа. В отличие от кинетической модели активного типа, в которой разрушение элементов происходит под действием только растягивающих напряжений, в модели хрупкого разрушения учитываются как растягивающие, так и сжимающие компоненты напряжений. Следовательно, динамический предел текучести σ в модели хрупкого разрушения зависит как от сжимающих компонент напряжений (2), так и от растягивающих (3):
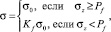 (2)
(2)
где σz – компонента напряжения в ударной волне (σz < 0 при сжатии), Pf – константа материала (Pf < 0), а коэффициент Kf может быть изменён от 0 до 1.
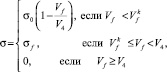 (3)
(3)
где V4, 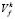 , σf – константы [12].
, σf – константы [12].
Модели разрушения активного и хрупкого разрушения работоспособны в период распространения ударных волн (области сжатия) и волн разгрузки (области растяжения). При интенсивном взаимодействии и деформировании контактирующих тел применяется модель разрушения эрозионного типа. В ней критерием разрушения служит критическое значение удельной энергии сдвиговых деформаций Esh. Текущее значение этой энергии определяется формулой
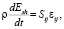 (4)
(4)
где Sij – компоненты девиатора тензора напряжений, εij – компоненты тензора скоростей деформаций.
Критическая величина удельной энергии сдвиговых деформаций выбирается зависящей от условий взаимодействия:
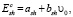 (5)
(5)
где υ0 – начальная скорость удара, ash и bsh – константы.
Когда в расчетной ячейке выполняется условие Esh > 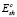 , эта ячейка считается разрушенной согласно модели разрушения эрозионного типа и удаляется из дальнейшего расчета, а параметры соседних ячеек корректируются с учетом законов сохранения, то есть масса расчетных узлов также должна быть уменьшена на величину массы разрушенного материала.
, эта ячейка считается разрушенной согласно модели разрушения эрозионного типа и удаляется из дальнейшего расчета, а параметры соседних ячеек корректируются с учетом законов сохранения, то есть масса расчетных узлов также должна быть уменьшена на величину массы разрушенного материала.
Рассматривается осесимметричная задача высокоскоростного взаимодействия ударника из высокопрочной стали, имеющего оживальную форму головной части, с многослойной композиционной преградой. Для решения задачи используется метод конечных элементов.
Результаты исследования и их обсуждение
Численно моделировалось взаимодействие многослойной преграды Ti – Al3Ti, состоящей из шести композитных слоев, общей толщиной ≈ 7 мм, с осредненной плотностью 3513,32 кг/м3 c ударником из высокопрочной стали. Соотношение толщин слоев интерметаллида к титановому сплаву в композитном слое составляет ≈ 4/1. Диаметр ударника 4,2 мм, длина 14,5 мм. Начальная скорость ударника варьировалась. Расчеты проводились при скоростях 2000, 3000 и 5000 м/с. В преграде реализовано неравномерное разбиение и, так как задача решалась в осесимметричной постановке, оно реализовано вдоль радиуса преграды, при этом размер элементов увеличивается по мере удаления от области взаимодействия. Константы моделей можно найти в [11].
Критическая величина удельной энергии сдвиговых деформаций (5) зависит от условий взаимодействия и задается функцией начальной скорости удара, следовательно, её значение для каждого материала варьировалось при различных начальных скоростях ударника. Значения критической величины энергии сдвиговых деформаций для трех материалов, используемых в расчете, представлены в таблице.
Значения критической величины энергии сдвиговых деформаций 
|
????0, м/с |
|
||
|
Высокопрочная сталь (ash = 3330 Дж/кг; bsh = 0,33) |
Al3Ti (ash = 1000 Дж/кг; bsh = 0,5) |
BT6 (ash = 3170 Дж/кг; bsh = 0,167) |
|
|
2000 |
3960 |
2000 |
3500 |
|
3000 |
4290 |
2500 |
3670 |
|
5000 |
4950 |
3500 |
4000 |
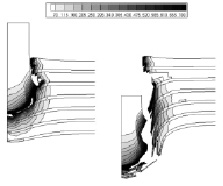
При начальной скорости ударника, равной 2000 м/с, к моменту времени 5,5 мкс (рис. 1, а) во втором композитном слое внутри интерметаллида зарождается макротрещина. Макротрещина начинает расти и к моменту откола части тыльной поверхности преграды, соответствующему 10,5 мкс (рис. 1, б), в данном слое образуется магистральная макротрещина.
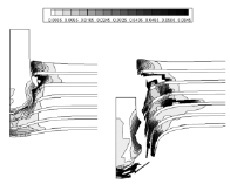
На рис. 2 показана степень поврежденности преграды и отчетливо видна тенденция роста макротрещин в слоях интерметаллида. Более интенсивному росту трещин препятствуют слои из титанового сплава. К моменту времени окончания взаимодействия преграды и ударника происходит расслоение преграды. При 2000 м/с повреждения в сечении преграды будут иметь конусообразный вид, что характерно для хрупкого разрушения.
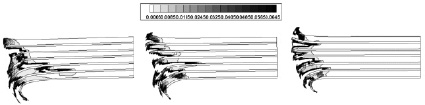
С ростом начальной скорости ударника возрастает роль ударно-волновых процессов, распространяющихся в преграде, и под действием волн разгрузки происходит ее расслоение (рис. 3). Стоит отметить, что при увеличении начальной скорости удара степень расслоения преграды увеличивается. При этом расслоение многослойного металло-интерметаллидного композита происходит за счет формирования макротрещин в интерметаллидных слоях.
а) б)
Рис. 1. Поля удельной энергии сдвиговых деформаций (кДж/кг) при начальной скорости удара 2000 м/с: а) в момент времени 5,5 мкс; б) в момент времени 10,5 мкс
а) б)
Рис. 2. Поля удельного объема микроповреждений (см3/г) при начальной скорости удара 2000 м/с: а) в момент времени 5,5 мкс; б) в момент времени 10,5 мкс
а) б) в)
Рис. 3. Поля удельного объема микроповреждений (см3/г) в преградах, взаимодействующих с ударниками с различными начальными скоростями: а) 2000 м/с; б) 3000 м/с; в) 5000 м/с
При относительно низких скоростях удара (700–1100 м/с [6, 11]) роль ударно-волновых процессов значительно ниже, и поэтому больший вклад в разрушение преграды вносят деформационные растягивающие нагрузки, действующие при внедрении ударника, а не волны разгрузки. Но при этом области с большими значениями удельного объема микроповреждений проявляются в слоях интерметаллида, а титановые слои, как и в случае более высоких скоростей удара, препятствуют распространению магистральных трещин [13].
Уменьшение скорости движения ударника после взаимодействия с преградой (запреградная скорость) зависит от начальной скорости его движения (рис. 4). При начальной скорости удара, равной 2000 м/с, запреградная скорость ударника уменьшается на 35 %, при 3000 м/с уменьшается примерно на 17,5 %, а при начальной скорости движения ударника, равной 5000 м/с, его запреградная скорость уменьшается на 6,3 %.
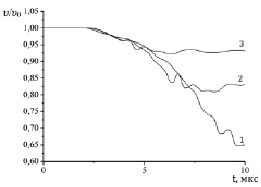
Рис. 4. Зависимость безразмерной величины / υ0, выражающей отношение скорости тыльной части ударника к его начальной скорости, от времени процесса взаимодействия, при различных начальных скоростях удара: 1 – 2000 м/с, 2 – 3000 м/с, 3 – 5000 м/с
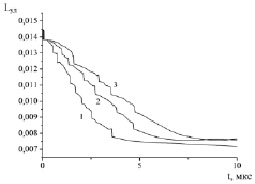
Рис. 5. Зависимость длины ударника от времени для различных начальных скоростей удара: 1 – 2000 м/с, 2 – 3000 м/с, 3 – 5000 м/с
В процессе взаимодействия с преградой ударник разрушается (срабатывается), что приводит к уменьшению его длины. На рис. 5 видно, что скорости изменения длины ударника для различных начальных скоростей удара разные, но после взаимодействия с преградой длина ударника Lуд, во всех трех случаях изменяется примерно на одну величину, разность длин к 10 мкс составляет 0,69–3,44 %. Длина ударника после взаимодействия с преградой в рассматриваемом диапазоне скоростей удара уменьшается примерно в 2 раза.
Заключение
Результаты численного моделирования деформирования и разрушения МИСКМ Ti-Al3Ti показывают, что с ростом начальной скорости удара в исследуемом диапазоне скоростей 2000–5000 м/с возрастает роль ударно-волновых процессов в характере разрушения преграды. В отличие от более низких скоростей удара, при которых больший вклад в характер разрушения многослойной преграды вносит деформационный фактор, действующий в области внедрения ударника, при более высоких скоростях происходит расслоение преграды, вызванное действием волн разгрузки. В интерметаллидных слоях металло-интерметаллидной композиционной преграды наблюдается расслоение вдоль границ со слоями из титана, причем степень расслоения возрастает с ростом скорости удара.
Библиографическая ссылка
Зелепугин С.А., Попов А.А. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ РАЗРУШЕНИЯ МНОГОСЛОЙНЫХ МЕТАЛЛО-ИНТЕРМЕТАЛЛИДНЫХ КОМПОЗИТОВ ПРИ СКОРОСТЯХ УДАРА ДО 5000 М/С // Современные наукоемкие технологии. 2019. № 2. С. 57-62;URL: https://top-technologies.ru/ru/article/view?id=37409 (дата обращения: 17.01.2026).
DOI: https://doi.org/10.17513/snt.37409




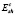 , Дж/кг
, Дж/кг