Повышение объема и уровня требований к радиолокационным системам (РЛС), особенно в части обеспечения защищенности от влияния поражающих факторов оружия, ставит перед разработчиками ряд принципиально новых научно-технических задач. К их числу относятся задачи количественной оценки на этапе проектирования стойкости к внешним воздействиям функциональных элементов, устройств и РЛС в целом. Анализ известных работ свидетельствует о том, что для данных условий построение математических моделей антенно-волноводных трактов (АВТ) РЛС не проводилось [1–3].
Практическая необходимость разработки указанных моделей определяется тем, что АВТ ряда РЛС содержат большое число равномерно изогнутых волноводов в Е- и Н-плоскостях (рисунок, таблица). В частности, в типовых РЛС отношение 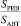 уязвимой площади равномерно изогнутых волноводов SРИВ к уязвимой площади АВТ в целом SАВТ составляет 11–40 %. В силу этого вероятность осколочного поражения равномерно изогнутых волноводов становится сравнимой с вероятностью поражения регулярных элементов и всего АВТ в целом.
уязвимой площади равномерно изогнутых волноводов SРИВ к уязвимой площади АВТ в целом SАВТ составляет 11–40 %. В силу этого вероятность осколочного поражения равномерно изогнутых волноводов становится сравнимой с вероятностью поражения регулярных элементов и всего АВТ в целом.
Цель статьи состоит в разработке математических моделей и алгоритмов количественного оценивания изменений радиотехнических параметров АВТ при повреждении равномерно изогнутых волноводов поражающими факторами оружия. В статье исследуются два основных типа повреждений – пробоины и вмятины. Моделирование повреждений АВТ проводилось в рамках экспериментально-теоретического метода на имитационной модели. Суть данного метода заключается в определении следующих величин:
– математического ожидания числа повреждений, их вида, места появления, размеров;
– радиотехнических параметров антенно-волноводных трактов с повреждениями;
– степени ухудшения тактико-технических характеристик РЛС за счет полученных элементами АВТ повреждений.

Внешний вид антенно-волноводного тракта РЛС 5Н87
Данные по равномерно изогнутым волноводам в типовых РЛС
|
Типы РЛС |
Количество равномерно изогнутых волноводов |
|
|
5Н87 |
134 |
40 |
|
5Н69 |
134 |
30 |
|
П-37 |
45 |
25 |
|
П-40 |
27 |
25 |
|
ПРВ-16 |
21 |
20 |
|
ПРВ-17 |
12 |
20 |
|
ПРВ-9 |
11 |
15 |
|
ПРВ-13 |
6 |
11 |
Материалы и методы исследования
Для оценивания изменений тактико-технических характеристик РЛС за счет повреждений АВТ принят обобщенный показатель эффективности, в качестве которого было выбрано отношение сигнал/шум (ОСШ) на выходе согласованного фильтра. Для количественной оценки влияния повреждений элементов АВТ на его радиотехнические параметры получен частный показатель эффективности, в качестве которого был выбран коэффициент полезного действия (КПД) АВТ КАВТ, который отличается от известных дополнительным учетом потерь на излучение из возникающих пробоин:
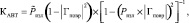 (1)
(1)
где 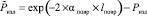 ;
;
Ризл – мощность излучения из пробоин;
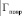 – модуль комплексного коэффициента отражения в АВТ с повреждениями;
– модуль комплексного коэффициента отражения в АВТ с повреждениями;
αповр – численное значение коэффициента затухания, обусловленного конечной проводимостью стенок АВТ с повреждениями;
lповр – длина частично поврежденных АВТ.
Для оценивания влияния повреждений разработаны соответствующие математические модели. При этом построение моделей проведено при следующих допущениях:
– рассмотрены только такие электромагнитные поля, для которых уравнения Максвелла могут быть сведены к волновому уравнению Гельмгольца;
– заполняющая волновод среда однородна, изотропна и без потерь, а стенки волновода обладают идеальной проводимостью;
– размеры широкой и узкой стенок поперечного сечения волновода выбраны такими, что распространяющейся является лишь одна основная волна [4, 5].
Указанные допущения позволили представить АВТ с повреждениями каскадным соединением четырехполюсников, каждый из которых описывает соответствующий регулярный и нерегулярный элементы АВТ с повреждениями. При этом показано, что разработка математических моделей нерегулярных элементов с повреждениями сводится к определению элементов соответствующей волновой матрицы передачи:
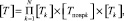 (2)
(2)
где [Tk] и [Tповрk] – матрицы передачи соответственно k-го неповрежденного и поврежденного участков элемента АВТ;
N – число повреждений.
В основу построения математических моделей равномерно изогнутых волноводов с вмятинами и пробоинами положено совместное применение метода эквивалентных схем сверхвысоких частот (СВЧ) и вариационных методов в электродинамике. При построении моделей обоснована возможность принятия допущения о том, что максимальные размеры вмятин Rвм и пробоин Rпроб много меньше рабочей длины волны λ современных РЛС (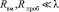 ). Обоснование данного допущения позволило использовать для построения искомых электродинамических моделей методы теории дифракции электромагнитных волн на малых телах и апертурах. Определение параметров математических моделей нерегулярных элементов с повреждениями проведено на основе решения соответствующих граничных задач для уравнений Максвелла в квазистатическом приближении.
). Обоснование данного допущения позволило использовать для построения искомых электродинамических моделей методы теории дифракции электромагнитных волн на малых телах и апертурах. Определение параметров математических моделей нерегулярных элементов с повреждениями проведено на основе решения соответствующих граничных задач для уравнений Максвелла в квазистатическом приближении.
Математическая модель равномерно изогнутого волновода с пробоиной
Равномерно изогнутый волновод с пробоиной был представлен каскадным соединением двух четырехполюсников с эквивалентной схемой в виде шунта из активного сопротивления и одним реактивным четырехполюсником с Т-образной эквивалентной схемой. Причем реактивный четырехполюсник учитывает потери на отражение электромагнитной энергии, а остальные два – потери на излучение электромагнитной энергии через пробоину в пространство. Параметры эквивалентных схем этих четырехполюсников определены при решении вариационными методами интегральных уравнений с учетом граничных условий непрерывности на апертуре пробоины нормальной составляющей электрического поля и скалярного магнитостатического потенциала. Задача определения [Tповрk] для модели (2) в случае пробоины на широкой стенке равномерно изогнутого волновода сведена к определению коэффициента отражения от пробоины Гпроб и отношения 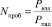 , где Рпад и Ризл – уровни мощности, распространяющейся в волноводе, и мощности, излученной через пробоину:
, где Рпад и Ризл – уровни мощности, распространяющейся в волноводе, и мощности, излученной через пробоину:
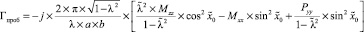 , (3)
, (3)
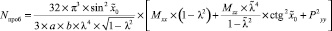 , (4)
, (4)
где 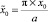 ;
; 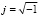 ;
;
 – нормированная длина волны,
– нормированная длина волны, 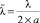 ;
;
x0 – координата центра повреждения на широкой стенке равномерно изогнутого волновода;
Pyy – коэффициент электрической поляризуемости пробоины;
Mxx, Mzz – компоненты тензора магнитной поляризуемости пробоины;
a, b – размер соответственно широкой и узкой стенки равномерно изогнутого волновода.
Математическая модель равномерно изогнутого волновода с вмятиной
Равномерно изогнутый волновод с вмятиной представлен реактивным четырехполюсником с эквивалентной схемой в виде шунта. Методом теории эквивалентных схем СВЧ получено соотношение для искомой модели [Tповрk] через коэффициент отражения Гвм, который определяется путем решения вариационными методами интегрального уравнения для касательной компоненты полного магнитного поля с учетом граничного условия исчезновения на поверхности вмятины касательной компоненты полного электрического поля:
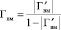 , (5)
, (5)
где
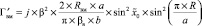 .
.
Здесь 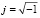 ;
;
β – волновое число в неограниченной среде – 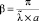 ;
;
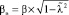 ;
;
Rвм – глубина вмятины.
Результаты исследования и их обсуждение
Средний уровень отражений и рабочего затухания в равномерно изогнутых волноводах с повреждениями на 25–30 % выше, чем в регулярных волноводах с такими же повреждениями. Проведено оценивание ожидаемых повреждений при применении противником по РЛС типовых боеприпасов. В результате разрыва боевой части противорадиолокационного снаряда типа «Шрайк» на расстоянии 5 м от РЛС 5Н87 следует ожидать около 90 повреждений АВТ (в том числе около 40 повреждений равномерно изогнутых волноводов). Указанные повреждения приведут к снижению ОСШ и уменьшению дальности обнаружения около 50 % (при том гипотетическом условии, что остальные системы РЛС повреждены не будут). Данные результаты моделирования получены в предположении исправной работы всех функциональных устройств и систем РЛС, за исключением АВТ.
Предложены технические решения [6, 7] адаптивных АВТ РЛС, которые могут позволить повысить ОСШ по сравнению с известными в условиях осколочно-пулевого воздействия: покрытие волноводного тракта снаружи токопроводящей эластичной оболочкой, обладающей способностью затягивать образующиеся в результате осколочно-пулевого воздействия механические пробоины и тем самым восстанавливать в местах повреждений электродинамические свойства волноводного тракта [6]; построение АВТ на основе автоматических корректоров амплитудно-частотных характеристик, позволяющих частично или полностью устранить рассогласование входа и выхода АВТ в достаточно широком диапазоне частот, вызванное механическими пробоинами и/или вмятинами [7].
Заключение
Разработанные математические модели волноводов отличаются от известных дополнительным учетом потерь на излучение из возникающих пробоин и потерь на отражение от пробоин и вмятин. Указанные математические модели являются достаточно эффективными и точными, а их применение целесообразно на этапе проектирования АВТ перспективных РЛС. Предложенные технические решения [6, 7] адаптивных АВТ РЛС могут позволить повысить ОСШ по сравнению с известными в условиях осколочно-пулевого воздействия, улучшая тем самым приём полезного сигнала.
Библиографическая ссылка
Гурский С.М. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ЭЛЕМЕНТОВ АНТЕННО-ВОЛНОВОДНЫХ ТРАКТОВ РАДИОЛОКАЦИОННЫХ СИСТЕМ С ПОВРЕЖДЕНИЯМИ // Современные наукоемкие технологии. 2019. № 2. С. 43-46;URL: https://top-technologies.ru/ru/article/view?id=37406 (дата обращения: 17.01.2026).
DOI: https://doi.org/10.17513/snt.37406




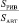 , %
, %