Методы оценивания параметров сигналов, числовых последовательностей и данных применяются в различных сферах деятельности: в распознавании речи, обработке технической информации, в анализе и предсказании значений биржевых котировок [1]. Существует множество прикладных пакетов для анализа больших данных: SPSS, Stadia, Matlab, Statistica, однако следует выделить пакет языка R – свободно распространяемый программный продукт с большим количеством пакетов и расширений, позволяющих существенно расширить область применения. В данной статье рассматривается применение пакетов языка R при анализе и предсказании значений биржевых котировок с использованием скрытых марковских моделей.
Цель исследования: рассмотрение возможности использования скрытых марковских моделей при анализе цены финансовых инструментов и прогнозировании движения цены.
Материалы и методы исследования
Скрытые марковские модели находят свое применение при разработке торговых рыночных моделей и стратегий [2]. При разработке торговых моделей необходимо выбрать какие-либо рыночные данные data и сгенерировать совокупность признаков O. В сфере фондовых рынков в качестве набора данных могут служить цены финансовых инструментов, а в качестве признаков могут выступать производные математические параметры, индикаторы технического анализа. Скрытая марковская модель определяет тот класс, который согласно методу максимального правдоподобия наиболее точно соответствует совокупности признаков O. Допустим, класс φ наиболее точно соответствует классу data, рассчитывается следующим образом:
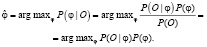
Вероятность P(O) не влияет на итоговый результат, поскольку от нее не зависит вычисление максимума функции. Вероятность P(O|φ) можно классифицировать таким образом, как вероятность принадлежности совокупности признаков O классу data, P(O|φ) определяется скрытыми состояниями марковской модели.
На рис. 1 изображена схема скрытой марковской модели, у которой пять состояний N; ai,j обозначает вероятность перехода из одного состояния в другое; bj(O) – обозначает вероятность нахождения массива параметров O при нахождении в состоянии j (необходимо учитывать, что j не может равняться первому и последнему (пятому) состоянию).
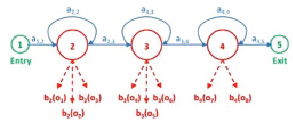
Рис. 1. Схема скрытой марковской модели
Таким образом, вектор параметров марковской модели определяется как β = [N, ai,j, bj]. Здесь O = [o1, o2, …., oT] – совокупность признаков, являющихся параметрами наблюдения; S = S [s1, s2, …., sT] – полученная последовательность состояний системы. Совместная вероятность соответствия вектора O вектору S при параметрах β будет равна произведению вероятности перехода из одного состояния в последующее и вектора параметров, которые генерируются при данном состоянии:
P(O, S|β) =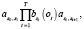 
где s0 и sT+1 являются начальными и конечными состояниями системы соответственно [3]. Совокупность состояний S является скрытой переменной, она нам не известна. Однако если вычислить сумму вероятностей по всем возможным состояниям, получим следующее выражение:
P(O|β) =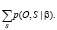 
Форвардный алгоритм рассчитывает полученную моделью вероятность данных по всем возможным состояниям. Вектор O описывается мультивариантным нормальным распределением. Для описания нормального распределения следует рассчитать, используя метод максимального правдоподобия, значения среднего распределения σ и ковариацию Cov вектора параметров. Чтобы рассчитать данные параметры для j-го состояния системы, применяется сегментация Витерби путем поиска жесткого соответствия вектора параметров, и состояний, которые генерировали данный вектор. Каждое состояние j генерирует наблюдения начиная с tj:
,
= 
.
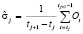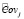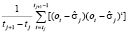С помощью форвардного метода эффективно рассчитывается функция P(O|β), где самой форвардной переменной считается вероятность того, что модель сгенерирует наблюдения до времени t. В момент времени t состояние j будет определяться следующим образом:
αj(t) = p(o1, o2, …., oT, s(t – 1) = k,
s(t) = j|β) = αk(t – 1) akj bj (Ot) =
= 
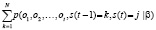
и вычисляется рекурсивно через переменную в момент t – 1 в состоянии k. Здесь: akj – вероятность перехода системы из k-го состояния в j-е состояние; bj(ot) – вероятность генерации вектора ot из состояния t. Схема алгоритма:
1. Инициализируем алгоритм: α1(0) = 1, αj(0) = 0 для 1 < j ≤ N и α1(t) = 0 для 1 < t ≤ T.
2. Описание рекурсии: при t = 1,2,...,T; при j = 2,3,..., N – 1; αj(t) = bj(ot)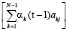 
.
3. Поиск решения: P(O|β) =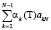 
.
Метод Витерби предназначен для аппроксимации P(O|β) вероятностью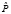 
(O|β), она рассчитывается по наиболее вероятной последовательности.
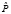(O|β) = maxs[p(O,S|β)],
где S – более вероятная последовательность состояний системы. Форвардная переменная рассчитывается данным способом:
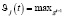p(o1, o2, …., ot, s(t) = j | β) =
= 
,
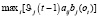где St-1 будем называть наилучшим путем. Алгоритм будет следующим:
1. Инициализируется алгоритм: ϑ1(0) = 1; ϑj(0) = 0 для 1 < j ≤ N и σ1(t) = 0 для 1 ≤ t ≤ T.
2. Описание рекурсии: при t = 1,2,...,T, j = 2,3,...,N – 1; ϑj(t) = max1≤k<N [ϑk(t – 1)akj]bj(ot); затем сохраняется предыдущее значение в переменной pred(j,t) = k.
3. Поиск решения: P(O, S|β) = max1≤k<N ϑk(T)akN, предыдущее значение сохраняем pred(N,T) = k. Лучший путь ищется, следуя в обратном порядке по сохраненным значениям pred(j,t).
Напрямую вычисляя Р(O|β), можно прийти к ошибкам малой разрядности, возникающим из-за ограниченных вычислительных возможностей компьютера, поэтому рекомендуется рассчитывать натуральный логарифм log(Р(O|β)).
Режимы могут распознаваться с помощью марковской модели двумя способами. При первом способе используется одна модель, в которой каждое состояние соответствует режиму, в котором находится финансовый инструмент. Другой способ – строить несколько моделей, где каждая модель предназначена лишь для одного режима, и необходимо отобрать именно ту модель, чья генерация данных наиболее точно соответствует текущему состоянию рыночного инструмента.
Результаты исследования и их обсуждение
Приведенные алгоритмы для описания и применения модели Маркова при анализе данных, а также ее элементы реализуются в библиотеке языка R RHmm (load.packages('RHmm')) [4]. Тренд рыночного инструмента считаем двух видов: растущий и падающий. Модель обучается путем симулирования исходных данных посредством нормального распределения, в котором M – медиана, σ – среднеквадратичное отклонение распределения. Для этого генерируются 100 значений приращений цены финансового инструмента для растущего тренда R(M.rost, σ.rost), 100 значений для нисходящего тренда R(M.pad, σ.pad). Еще 100 значений сгенерированы для растущего тренда с другими значениями медианы и среднеквадратичного отклонения. Интервал между приращениями цены будем считать равным одному дню. Для примера ниже указана часть кода программы на языке R, которая осуществляет поиск режимов и определяет их вероятности: z = c(rost, pad, rost_2; ResFit = HMMFit(z,nStates=2); Vitterbi= viterbi(ResFit,z); Forvard_Model = forwardBackward(ResFit,z).
На рис. 2 изображено моделирование работы алгоритма, основанного на первой модели. Для демонстрации работы программы мы обучаем модель на первых 300 отсчетах (днях), затем тестируем на следующих 300 отсчетах (днях). Для построения графика использовался пакет языка R «quantmod» [5].
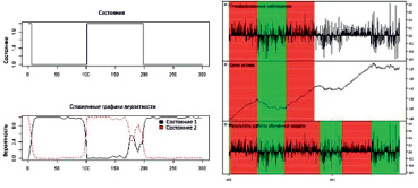
Рис. 2. Демонстрация работы алгоритма, основанного на построении одной модели
Здесь: слева представлены заданные режимы (состояния), которые использовались для генерирования приращений цены, и вероятность того, что система находится в каком-либо из этих состояний (по горизонтальной оси отложены порядковые номера дней); справа представлены сгенерированные наблюдения (первые 300 значений предназначены для обучения системы, последние 300 для тестирования); цена финансового инструмента, для того, чтобы визуально наблюдать вид тренда; изображены результаты работы программы. Красным цветом для удобства задается нисходящий тренд (на двух верхних графиках справа), зеленым цветом задается восходящий тренд (на двух верхних графиках справа). На нижнем графике представлено то, как программа определяет данные режимы согласно заданному алгоритму. После проведения тестирования на всей истории данного финансового инструмента с 1921 г. установлено, что погрешность определения алгоритмов границ режимов составляет не более 14,23 % по сравнению с шириной интервала. Аналогичные действия были выполнены при моделировании работы второго метода, в котором строятся несколько моделей, где каждая модель предназначена лишь для одного режима.
Протестируем работу алгоритма на примере графиков биржевых фьючерсов RTS-9.15. Для тестирования использовалась программа, написанная при помощи языка C#, с использованием библиотеки Accord.net. Количество входных биржевых «свечей» (временных интервалов) – изменяемый параметр, вторым параметром является горизонт прогноза. Временной интервал «свечи» зависит от данных, загруженных в текстовый документ. Программа рассчитывает вероятность верного предсказания в пределах указанного горизонта, прибыль в процентах, максимальную просадку.
Исходная последовательность цен делится в пропорции 70/30: первые 70 % значений используются для обучения модели, оставшиеся 30 % для проверки эффективности, проверки устойчивости оценивания модели и отсутствия подгонки. Результат представлен на рис. 3. В качестве анализируемого инструмента используется фьючерс RTS-9.15, временной интервал последовательности с 16 июня 2015 г. по 16 июля 2015 г., временной интервал «свечей» 5 мин.
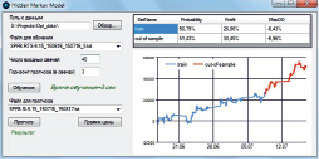
Рис. 3. Результат работы алгоритма при анализе фьючерса RTS-9.15
Здесь: «train» – обучающая последовательность равная первым 70 % значениям; «out-of-sample» – тестовая выборка для проверки устойчивости алгоритма, последние 30 % значений; на графике изображены кумулятивные приращения цены фьючерса в зависимости от даты; горизонт прогноза установлен равным 3 «свечам», или 15 мин; вероятность прогноза на обучающей последовательности равна 50,79 %, при доходности в 26,86 %; вероятность прогноза на тестовой последовательности снизилась до 51,43 %, однако доходность составила порядка 30,45 %; максимальная просадка на тестовой последовательности составила порядка 6,96 %.
Для проверки анализируются результаты алгоритма на следующем временном интервале с 17 июля 2015 г. по 16 августа 2015 г. без повторения процесса обучения, а также на ином финансовом инструменте, для примера используем фьючерс Si-9.15. Используемые фьючерсы являются самыми ликвидными на российском фондовом рынке FORTS, поэтому именно они были выбраны с целью минимизации случайной компоненты и минимизации эффекта волатильности рынка. Модели тестируются на двух различных активах и на двух временных интервалах, имеют различные длительности трендов, чередования трендовых и флэтовых движений, на данных интервалах наблюдались все три возможных режима модели [6]. В таблице представлена оценка результатов работы модели в сравнении между двумя активами, каждый актив оценивался на двух временных интервалах после процесса обучения модели.
При тестировании скользящего окна модели (при каждом движении окна модель переучивается) для фьючерса Si-9.15 вероятность составила 51,21 %, доходность составила 8,48 %, максимальная просадка составила 6,38 %, что говорит о снижении волатильности просадки.
Результат тестирования программы на примере фьючерсов
|
Фьючерс |
Начало временного интервала |
Конец временного интервала |
Вероятность прогноза, % |
Доходность, % |
Макс. просадка, % |
|
RTS-9.15 |
16 июня 2015 г. |
16 июля 2015 г. |
51,43 |
30,45 |
6,96 |
|
RTS-9.15 |
17 июля 2015 г. |
16 августа 2015 г. |
48,95 |
30,98 |
11,45 |
|
Si-9.15 |
16 июня 2015 г. |
16 июля 2015 г. |
57,06 |
11,68 |
4,52 |
|
Si-9.15 |
17 июля 2015 г. |
16 августа 2015 г. |
54,17 |
20,58 |
17,95 |
Выводы
Внедрение в процесс торговли механизмов прогнозирования позволяет существенно улучшить качество прогнозов, а использование пакетов свободно распространяемого языка R позволит трейдерам самостоятельно дорабатывать алгоритм под собственные потребности. Были выявлены недостатки работы программы – диапазон применяемых параметров узок, при их изменении на 20–30 % прогноз предсказания может привести к резкому снижению вероятности прогнозирования. Вероятность прогнозов на уровне 50–55 % в условиях реальной торговли на фондовом рынке является ниже рекомендуемых 70 % профессиональными трейдерами для ее применения из-за биржевых комиссий. C целью повышения устойчивости и эффективности алгоритма необходимо добавить параметры, не связанные с ценой, например биржевой «стакан заявок», значения объемов торгов, а также верно выбрать статистическое распределение. В исследовании использовалось нормальное распределение.
Достоинствами использования скрытых марковских процессов является высокая доходность и вероятность прогноза выше 50 %, даже при использовании в качестве исходных данных только последовательности цен, следует добавить неценовые параметры в алгоритм. Об устойчивости модели говорят близкие значения параметров при использовании алгоритма на разных временных интервалах и разных финансовых инструментах. При отдалении интервала применения алгоритма от обучающей последовательности снижается вероятность прогноза и увеличивается максимальная просадка. Использование скользящего окна показало снижение доходности, но большую стабильность и снижение рисков. Максимальная просадка снизилась практически в два раза до 6,38 %, что существенно снижает риски потери средств трейдерами. Путем задания интервала прогнозирования и числа входных «свечей» находятся оптимальные параметры алгоритма с точки зрения качества прогнозирования и снижения рисков. Скрытые марковские модели проявили высокий потенциал для применения их в торговле на фондовых рынках, были показаны способы модернизации программы.
Библиографическая ссылка
Алюнов Д.Ю., Мытникова Е.А., Мытников А.Н. ИСПОЛЬЗОВАНИЕ ЯЗЫКА R ПРИ СТАТИСТИЧЕСКОМ АНАЛИЗЕ ДАННЫХ // Современные наукоемкие технологии. – 2018. – № 11-2. – С. 168-172;URL: https://top-technologies.ru/ru/article/view?id=37297 (дата обращения: 22.12.2024).