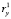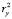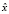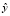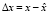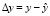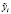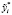Кластерный анализ и отдельные его элементы достаточно часто используются при решении задач распознавания образов [1–3]. С помощью этого аппарата удается, в рамках принятой метрики, сформировать более или менее плотные группировки в составе обучающей выборки, что позволяет заметно ускорить процедуру классификации. Однако в современных реалиях гипотеза о неизменности положения и границ построенных кластеров представляется малоправдоподобной. Действительно: изменения интенсивности и состава потоков, пополняющих обучающую выборку, миграция объектов между кластерами и т.д. могут стать причиной изменения как отдельных кластерных образований, так и структуры кластерного множества в целом.
В работе [4] был рассмотрен и проиллюстрирован на конкретном числовом примере саморазвивающийся алгоритм распознавания, позволяющий в пространстве классифицирующих признаков формировать кластеры и осуществлять корректировку их положения и размеров сообразно состоянию обучающей выборки. При этом, однако, давалось описание лишь результата действия изменений обучающей выборки и никак не исследовалось влияние их основной движущей силы – времени.
Цель статьи: разработка математической модели эволюционных изменений кластерных образований, используемых в задачах распознавания образов.
Методом исследования является аппарат анализа временных рядов.
Результаты исследования и их обсуждение
Пусть в фазовом пространстве классифицирующих признаков сформированы несколько последовательностей кластеров, заданных координатами центров своих кластерных сфероидов. Каждому кластеру поставлен в соответствие определенный момент времени 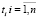 , на который вполне установлено положение его центра в соответствии с алгоритмом, подробно описанном в работе [4]. На рисунке приведен пример, где таких последовательностей три, а положения кластерных центров обозначены символами x, Δ, ?.
, на который вполне установлено положение его центра в соответствии с алгоритмом, подробно описанном в работе [4]. На рисунке приведен пример, где таких последовательностей три, а положения кластерных центров обозначены символами x, Δ, ?.
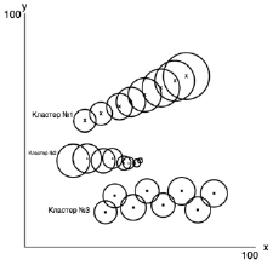
Пример расположения кластерных последовательностей
Таким образом, фактически, описанные выше последовательности представляют собой ряды динамики, уровни которых задаются не отдельными числами, а числовыми множествами, чьи мощности равны размерности пространства классифицирующих признаков. И если эта размерность равна m, то для построения модели поведения каждой кластерной последовательности необходимо получить m уравнений вида 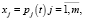 где xj – элементы множества признаков. Естественно, что чем больше число m, тем больше проблем может возникнуть при идентификации параметров модели и сложностей с интерпретацией результатов моделирования. Следовательно, эволюционные изменения каждой из выявленных кластерных последовательностей полностью характеризуются m временными рядами по количеству классифицирующих признаков исследуемой обучающей выборки.
где xj – элементы множества признаков. Естественно, что чем больше число m, тем больше проблем может возникнуть при идентификации параметров модели и сложностей с интерпретацией результатов моделирования. Следовательно, эволюционные изменения каждой из выявленных кластерных последовательностей полностью характеризуются m временными рядами по количеству классифицирующих признаков исследуемой обучающей выборки.
Как известно [5], значения уровней временных рядов формируются как результат совокупного действия трех составляющих: трендовой T, циклической S и случайной E. Поэтому анализ временных рядов рекомендуется начинать с оценки независимого вклада каждой из них. Это осуществляется путем построения коррелограмм или таблиц коэффициентов автокорреляции. Если будет выявлено, что преобладающее влияние на формирование уровней ряда имеет трендовая составляющая, то соответствующий классифицирующий признак признается значимо влияющим на ход эволюционных изменений кластерной последовательности. После этого устанавливается тип тренда и строится регрессионная модель, которая после должной статистической проверки может быть использована для прогнозирования дальнейших этапов эволюции. При наличии преобладающих трендовых составляющих у двух и более признаков следует проверить гипотезу коинтегрированности, то есть установить, являются ли выявленные тренды взаимообусловленными или нет. Для решения этой задачи могут быть использованы, например, метод отклонения от тренда [5], критерий Ингла – Грэнджера [6–8] и ряд других. Если гипотеза коинтегрированности нашла свое подтверждение, то совокупное влияние трендов соответствующих признаков должно быть обязательно учтено при прогнозировании эволюционного поведения кластерной последовательности. В противном случае сохранение трендовых тенденций в моменты времени, следующие за наблюдаемыми, не гарантировано и, следовательно, использование их в прогнозировании неправомочно.
В случае преобладания, или заметного присутствия во временном ряде какого либо признака с циклической составляющей, ее влияние должно быть элиминировано одним из известных методов [5]. В сглаженном таким образом временном ряду оценивается трендовая составляющая, неразличимая на фоне циклических изменений или обосновывается ее незначимость на ход эволюционного процесса. Если окажется, что влияние тренда существенно, его вклад учитывается в соответствии с описанной выше процедурой, иначе его следует рассматривать как шум – случайную составляющую с предположительно нормальным законом распределения. При этом действие, оказываемое соответствующим признаком на эволюцию, признается ничтожным.
Весьма важным показателем, характеризующим эволюционные преобразования кластерных последовательностей, является фактор, не принадлежащий пространству классифицирующих признаков: мощность множества элементов, входящих в состав кластера. Эта величина с течением времени может и должна меняться, поскольку количество элементов, принадлежащих кластеру, может как возрастать, так и убывать. Рост будет наблюдаться либо при захвате объектов из других кластеров, либо вследствие пополнения обучающей выборки в целом. Убыль же возможна по причине перехода части элементов в другие кластеры, а также в случае естественной или принудительной ликвидации каких-либо объектов. Если мощность множества элементов членов кластерной последовательности сохраняется на постоянном уровне, или имеет тенденцию к росту, это является свидетельством положительной эволюционной динамики, а кластер имеет ясные перспективы дальнейшего существования. Обратная тенденция говорит о деградации кластера вплоть до возможности его исчезновения, поэтому прогноз его эволюционных изменений неопределён и бесполезен.
Проиллюстрируем возможности описанного выше механизма и особенности его применения на демонстрационном примере. Рассмотрим ход эволюционных изменений трех кластерных сфероидов, заданных в двумерном пространстве классифицирующих признаков x и y (рисунок). Значения признаков, определяющих положение центров кластеров, в равноотстоящие друг от друга моменты времени предполагаются известными, так же как количество элементов, имеющихся в составе кластеров. Область изменения признаков приведена к размеру 100х100 условных единиц. Координаты кластерных центров, зафиксированные в моменты времени 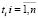 , а также мощности множеств элементов, входящих в состав кластеров, представлены в табл. 1.
, а также мощности множеств элементов, входящих в состав кластеров, представлены в табл. 1.
Таблица 1
Эволюционные изменения кластеров
|
время |
Кластер № 1 |
Кластер № 2 |
Кластер № 3 |
||||||
|
t |
Признак x |
Признак y |
Мощность N |
Признак x |
Признак y |
Мощность N |
Признак x |
Признак y |
Мощность N |
|
1 |
26 |
54 |
440 |
21 |
37 |
310 |
35 |
15 |
390 |
|
2 |
33 |
57 |
457 |
24 |
38 |
292 |
42 |
26 |
415 |
|
3 |
41 |
60 |
460 |
26 |
37 |
267 |
47 |
17 |
403 |
|
4 |
46 |
62 |
474 |
27 |
38 |
231 |
53 |
31 |
394 |
|
5 |
52 |
65 |
470 |
29 |
36 |
206 |
58 |
15 |
410 |
|
6 |
59 |
68 |
490 |
30 |
36 |
181 |
62 |
29 |
398 |
|
7 |
65 |
71 |
492 |
32 |
36 |
168 |
67 |
16 |
406 |
|
8 |
70 |
73 |
505 |
35 |
37 |
153 |
74 |
28 |
412 |
Анализ эволюционного поведения начнем с вычисления коэффициентов автокорреляции первого и второго порядка для рядов обоих классифицирующих признаков во всех трех кластерных последовательностях по формуле
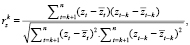 (1)
(1)
где k – порядок коэффициента автокорреляции, z – текущее значение классифицирующего признака, 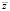 – среднее значение классифицирующего признака и оно равняется общему количеству значений признаков, деленному на число наблюдений. Результаты вычислений сведены в табл. 2.
– среднее значение классифицирующего признака и оно равняется общему количеству значений признаков, деленному на число наблюдений. Результаты вычислений сведены в табл. 2.
Таблица 2
Коэффициенты автокорреляции динамических рядов
|
Кластер № 1 |
Кластер № 2 |
Кластер № 3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,998 |
0,995 |
0,997 |
0,991 |
0,976 |
0,951 |
0,176 |
0,091 |
0,991 |
0,990 |
–0,793 |
0,931 |
Таблица 3
Расчет остатков регрессионных моделей
|
Время |
Наблюдаемые признаки |
Вычисленные признаки |
Остатки |
|||
|
t |
x |
y |
|
|
|
|
|
1 |
26 |
54 |
27 |
54,17 |
–1 |
–0,17 |
|
2 |
33 |
57 |
33,29 |
56,91 |
–0,29 |
0,09 |
|
3 |
41 |
60 |
39,58 |
59,65 |
1,42 |
0,35 |
|
4 |
46 |
62 |
45,87 |
62,39 |
0,13 |
–0,39 |
|
5 |
52 |
65 |
52,16 |
65,13 |
–0,16 |
–0,16 |
|
6 |
59 |
68 |
58,45 |
67,87 |
0,55 |
0,13 |
|
7 |
65 |
71 |
64,74 |
70,61 |
0,26 |
0,39 |
|
8 |
70 |
73 |
71,03 |
73,35 |
–1,03 |
–0,35 |
Из материалов этой таблицы видно, что в кластерной последовательности № 1 на ход эволюции преобладающее влияние по обоим признакам оказывает возрастающая трендовая составляющая. Однонаправленность трендов совершенно очевидна, и потому вопрос о том, является ли это проявлением сущностной связи между признаками или просто случайностью, представляется вполне актуальным. Для отыскания ответа на этот вопрос используем хорошо известный метод отклонения от тренда. Для рядов обоих признаков кластерной последовательности № 1 построим линейные регрессионные зависимости от времени. Используя процедуру метода наименьших квадратов, получим для признака x
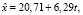 (2)
(2)
а для признака y
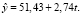 (3)
(3)
Проверка по критерию Фишера показала адекватность обоих уравнений регрессии, что является естественным для столь высоких значений коэффициентов автокорреляции первых двух порядков по каждому признаку первой последовательности кластеров. Далее рассчитываем значения признаков 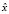 и
и 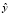 в точках
в точках 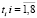 с помощью уравнений (2) и (3) и отыскиваем остатки. Результаты вычислений приведены в табл. 3.
с помощью уравнений (2) и (3) и отыскиваем остатки. Результаты вычислений приведены в табл. 3.
Находя значения коэффициентов автокорреляции первого порядка для остатков Δx и Δy, видим, что их величины 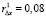 и
и 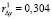 значительно меньше, нежели аналогичные коэффициенты
значительно меньше, нежели аналогичные коэффициенты 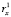 и
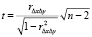
и 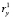 (табл. 2,кластер № 1). Это позволяет утверждать, что влияние трендов классифицирующих признаков x и y, ясно проявляющееся в кластерной последовательности № 1, полностью устранено. Вместе с тем для коэффициентов парной линейной корреляции rxy и rΔxΔy уровень значений сохраняется rxy = 0,996; rΔxΔy = 0,768. Некоторое снижение, конечно, есть, однако проверка по критерию Стьюдента
(табл. 2,кластер № 1). Это позволяет утверждать, что влияние трендов классифицирующих признаков x и y, ясно проявляющееся в кластерной последовательности № 1, полностью устранено. Вместе с тем для коэффициентов парной линейной корреляции rxy и rΔxΔy уровень значений сохраняется rxy = 0,996; rΔxΔy = 0,768. Некоторое снижение, конечно, есть, однако проверка по критерию Стьюдента
 (4)
(4)
показывает, что величина коэффициента rΔxΔy сохраняет статистическую значимость t = 2,45 > tkp = 2,26. Отсюда следует, что совпадение трендовых составляющих признаков x и y, описывающих эволюционные изменения центров первой кластерной последовательности, является не случайным, но есть проявление некоторой сущностной связи между ними. Это, в свою очередь, дает веские основания предполагать, что наблюдаемая связь между трендами может быть экстраполирована для прогнозирования последующих этапов эволюции кластера № 1. В целом, с учетом устойчивого возрастания мощности множества элементов, наполняющих этот кластер, следует оценить перспективы его дальнейшего развития как благоприятные.
Эволюционное поведение кластера № 2 практически полностью определяется влиянием ярко выраженной трендовой составляющей признака х. Другой классифицирующий признак на изменение положения центров кластерной последовательности не оказывает практически никакого воздействия, ибо в его ряду преобладает случайная составляющая (табл. 2). Величины коэффициентов автокорреляции 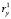 и
и 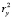 во второй кластерной последовательности очень малы, что позволяет считать влияние признака y на эволюционные изменения кластера № 2 ничтожными и воспринимать производимый им эффект как случайный шумовой фон. Следует отметить монотонное и довольно значительное падение мощности кластерообразующих множеств в этой последовательности. Это указывает на то, что кластер № 2 деградирует, перспективы его дальнейшего существования весьма неопределенны, а какие бы то ни было прогнозные предсказания сомнительны.
во второй кластерной последовательности очень малы, что позволяет считать влияние признака y на эволюционные изменения кластера № 2 ничтожными и воспринимать производимый им эффект как случайный шумовой фон. Следует отметить монотонное и довольно значительное падение мощности кластерообразующих множеств в этой последовательности. Это указывает на то, что кластер № 2 деградирует, перспективы его дальнейшего существования весьма неопределенны, а какие бы то ни было прогнозные предсказания сомнительны.
Эволюционное поведение кластера № 3, как видно из рисунка и табл. 2, определяется совокупным влиянием сильного возрастающего тренда признака х и отчетливо выраженной циклической составляющей динамического ряда признака y с периодом, равным двум лаговым единицам. Подобные явления достаточно типичны и могут наблюдаться, например, при изучении циклов солнечной активности, сезонных колебаний цен на некоторые виды товаров и т.п. Как отмечалось выше, анализ и прогнозирование подобных процессов требует применения специальных приемов, смысл которых состоит в оценке влияния циклической составляющей по каждому элементу цикла в отдельности. Для достижения этой цели осуществляется сглаживание уровней временного ряда с помощью скользящих средних по формуле
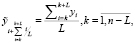 (5)
(5)
где L – длина периода циклической составляющей, выраженная в единицах временного лага.
Если число элементов периода L четно, то полученным значениям скользящих средних нельзя поставить в соответствие имеющиеся временные метки. Для устранения этого затруднения вычисляются центрированные скользящие средние 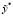 , как средние арифметические соседних значений скользящих средних. L элементов в результате этой операции теряются, однако впоследствии они будут восстановлены.
, как средние арифметические соседних значений скользящих средних. L элементов в результате этой операции теряются, однако впоследствии они будут восстановлены.
Принимая гипотезу об аддитивной структуре ряда признака y, находим оценку циклической составляющей для всех оставшихся уровней.
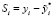 . (6)
. (6)
Поскольку в рассматриваемом примере длина цикла составляет две единицы временного лага, находим средние значения циклической составляющей для четных и для нечетных моментов времени 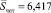 ,
, 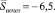 Величина поправки K для аддитивной модели ряда будет
Величина поправки K для аддитивной модели ряда будет
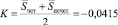 . (7)
. (7)
Таким образом, окончательные величины циклических компонент для четных и нечетных моментов времени будут 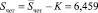 ,
, 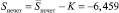 согласно гипотезы аддитивности
согласно гипотезы аддитивности
y = T + S + E, (8)
поэтому ряд признака y с элиминированной циклической составляющей y* для третьей кластерной последовательности определится из соотношения
y* = y – S. (9)
Результаты вычислений представлены в табл. 4.
Величина коэффициента автокорреляции первого порядка, вычисленная для ряда y*, 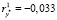 , указывает на полное отсутствие в этом ряду, а значит, и в ряду признака y трендовой составляющей. Следовательно, в ход эволюционных процессов кластера № 3 классифицирующий признак y вносит только регулярные циклические изменения. В целом, при сохранении условий внешней среды, перспективы дальнейшего существования кластера № 3 можно считать благоприятными. Мощность множества элементов, входящих в его состав, сохраняется на постоянном уровне с незначительными нерегулярными колебаниями, что говорит об отсутствии признаков деградации.
, указывает на полное отсутствие в этом ряду, а значит, и в ряду признака y трендовой составляющей. Следовательно, в ход эволюционных процессов кластера № 3 классифицирующий признак y вносит только регулярные циклические изменения. В целом, при сохранении условий внешней среды, перспективы дальнейшего существования кластера № 3 можно считать благоприятными. Мощность множества элементов, входящих в его состав, сохраняется на постоянном уровне с незначительными нерегулярными колебаниями, что говорит об отсутствии признаков деградации.
Таблица 4
Расчет сглаженного ряда признака y для кластера № 3
|
Время t |
yi |
Скользящее среднее
|
Центрированное скользящее среднее
|
Циклическая составляющая Si |
|
|
1 |
15 |
20,5 21,5 24 23 22 22,5 22 |
21,459 |
||
|
2 |
26 |
21 |
5 |
19,541 |
|
|
3 |
17 |
22,75 |
–5,75 |
23,459 |
|
|
4 |
31 |
23,5 |
7,5 |
24,541 |
|
|
5 |
15 |
22,5 |
–7,5 |
21,459 |
|
|
6 |
29 |
22,25 |
6,75 |
22,541 |
|
|
7 |
16 |
22,25 |
–6,25 |
22,459 |
|
|
8 |
28 |
21,541 |
Выводы
1. Построена математическая модель эволюционных изменений саморазвивающихся кластерных образований.
2. С помощью аппарата динамических рядов показана возможность прогнозирования хода их развития.
3. Некоторые возможности предлагаемой модели продемонстрированы на иллюстративном примере.
Библиографическая ссылка
Нуриев Н.К., Аль-Хашеди А.А., Печеный Е.А. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭВОЛЮЦИИ КЛАСТЕРНЫХ ОБРАЗОВАНИЙ // Современные наукоемкие технологии. 2018. № 8. С. 121-126;URL: https://top-technologies.ru/ru/article/view?id=37131 (дата обращения: 17.12.2025).
DOI: https://doi.org/10.17513/snt.37131




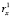
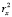
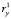
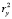
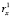
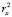
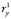
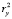
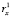
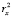 .
.