На сегодняшний день одним из основных видов контента, распространяемого через сети, является видео. С течением времени объемы передаваемых видеоданных неуклонно растут не только за счет все большего перехода пользователей от текстовых сообщений к аудио и видеопосланиям, но и за счет увеличения разрешения передаваемого изображения.
В то же время развивающиеся пиринговые технологии позволяют большему количеству клиентов, заинтересованных в получении контента, участвовать в передачи трафика, что снижает нагрузку на первичный источник данных. Для традиционного файлового обмена успешным примером такой технологии может служить технология BitTorrent, которая, однако, слабо приспособлена к передаче потоковых данных. При файловом обмене основной целью является минимизация времени скачивания данных целиком. Такая цель, как правило, достигается рандомизацией порядка получения блоков и запросом в первую очередь самых быстро доступных блоков.
Модель потоковой передачи данных через пиринговые сети отличается от принятого в файловом обмене тем, что блоки данных генерируются динамически и должны быть доставлены конечному получателю в том же порядке. Каждый узел пиринговой сети хранит некоторое количество полученных данных чтобы передавать их другим узлам через поддерживаемые соединения. Качество обслуживания при этом заключается в обеспечении минимальных задержек и отсутствии потерь при передаче данных.
Эффективность стриминговых сетей может обеспечиваться тремя различными механизмами: изменением объема передачи данных (в случаях, когда это возможно), планированием передачи, определяющей в какой момент времени какой блок должен быть передан какому соседу, и управлением структурой сети, обеспечивающей оптимальный набор соседей, то есть топологию сети. Так в работе [1] для сетей передачи видеопотоков предлагается изменять разрешение передаваемого изображения, тем самым снижая нагрузку на канал. При очевидной простоте и эффективности такого метода он имеет существенные недостатки: во-первых, узел, получающий видеоданные в низком качестве, не может являться источником качественных данных для других узлов, а во-вторых, узлы-источники при таком подходе должны производить перекодировку сигнала в реальном времени по требованию более слабых узлов, что ведет к увеличению вычислительной нагрузки на них. Существует несколько работ [2–4], в которых предлагаются различные алгоритмы, близкие к оптимальному, в сетях с топологией в виде полного графа, так как она позволяет выбирать узлы с наибольшей пропускной способностью среди всех узлов сети. Однако на практике реализация такого подхода затруднена, так как для поддержания большой полносвязной сети требуются значительные ресурсы. К тому же количество одновременных соединений для одного узла ограничено архитектурой современных IP-сетей, что требует еще большего увеличения объема трафика для поддержания связности и количество известных соседей становится одним из главных ограничений при определении структуры сети.
Таким образом, сеть распространения потоковых данных должна хорошо работать в следующих условиях:
- разная пропускная способность узлов;
- удаления (в том числе неожиданные) и добавления узлов из и в сеть;
- динамического изменения параметров пропускной способности отдельных узлов.
Цель исследования: в данной статье предлагается алгоритм, позволяющий обеспечить близкую к оптимальной с точки зрения пропускной способности структуру сети, состоящую из разнородных узлов. Предлагаемый алгоритм позволяет строить сеть без явного измерения ее пропускной способности. Вместо этого информация, необходимая для построения сети, рассчитывается на основе степени загруженности исходящих соединений каждого узла, что позволяет комплексно оценить его производительность, а не только пропускную способность сети.
Проблема построения оптимальных по структуре пиринговых сетей достаточно исследована, например, в [5, 6], но большинство решений могут быть реализованы только при централизованном управлении всеми узлами сети. Большинство же исследований [2, 3, 7] по оптимизации передачи данных основываются на предположении, что задержка при передаче блока в первую очередь определяется сетевыми задержками (RTT), а не ограничениями пропускной способности, что более распространено в современных сетях.
Принятые допущения
Предположим, что пиринговая система передает один видеопоток от источника к N узлам-потребителям. Узлы образуют множество P, а весь поток разделен на блоки размером S бит. Первичный источник генерирует блоки со скоростью λ и отправляет их некоторым узлам, которые, в свою очередь, передают блоки другим узлам, т.е. используется push-based схема, когда передача данных инициируется источником. Пропускная способность узлов сети на отправку данных ограничена, при этом пропускная способность приема достаточна для потока и, таким образом, не является ограничением. Как правило, скорость приема данных в пользовательских сетях выше скорости отправки, так что время передачи блока данных зависит только от скорости его отправки узлом-источником. Пропускную способность отправки узлом p определим как B(p), тогда время передачи блока будет равно S/B(p).
Наши узлы объединены в сеть, которую можно описать в виде направленного графа G(P, E), где (p, q)∈E, а E – множество соединений, где узел p может передавать данные узлу q, то есть q является соседом-получателем p, а p – соседом-источником q. Для каждого узла p определено множество соседей-получателей No(p), тогда |No(p)| – количество исходящих соединений. Определим также C(p) как множество косвенных соседей узла p. Таким образом, каждому узлу нашей сети известны только узлы, входящие в No(p) и C(p). При этом узлы могут независимо подключаться и отключаться от сети. Способ построения сети и алгоритм передачи описаны ниже.
Оптимизация структуры сети
В предлагаемом нами алгоритме адаптация структуры сети выполняется на основе локального принципа, то есть независимо каждым узлом, на основании данных из множеств No(p) и C(p). Каждые δ принятых блоков (временное окно) узел p изменяет количество исходящих соединений в большую или меньшую сторону. Решение принимается на основе того, какое количество соединений было активно в течение временного окна.
Если за время окна хотя бы один блок был послан узлом большему количеству своих соседей, то он может обслужить больше соседей и их число должно увеличиться на n+. Новые соседи выбираются из множества C(p).
Если за время окна данные были переданы по меньшему количеству соединений, значит, узел не может обслуживать столько соседей и их число нужно уменьшить на n–.
Число активных соединений показывает, какой вклад в работу сети может внести узел, и чем оно больше, тем больше соседей может обслужить узел, а значит, он должен быть расположен ближе к первичному источнику для уменьшения задержек в сети.
Цель алгоритма – держать количество соседей узла p немного больше, чем то количество соединений, которое он реально успевает обслужить. Количество соединений определяется балансом между двумя целями:
1) дать достаточно большое количество соседей чтобы полностью утилизировать пропускную способность,
2) сохранить затраты на поддержку сети на достаточно низком уровне.
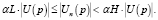 (1)
(1)
Пусть U(p) – множество использованных соединений, а Un(p) – множество неиспользованных. Цель алгоритма поддерживать соотношение (1), где αL, αH – нижняя и верхняя границы количества неиспользованных соединений в долях от количества использованных. При моделировании были эмпирически подобраны значения αL = 0,1 и αH = 0,3, дающие наилучшую структуру сети.
По окончании временного окна производится оценка количества неиспользованных соединений Un(p) для каждого узла и на ее основе принимается решение об изменении количества активных соединений. При этом выполняются следующие действия:
- если количество неиспользованных соединений меньше нижней границы, то устанавливаются новые соединения;
- если количество неиспользованных соединений больше верхней – закрывается часть неиспользуемых.
Для алгоритма так же определено минимальное количество исходящих соединений e = 1 и входящих f = 2 соединений, чтобы избежать ситуации отключения отдельных узлов от сети. Для предотвращения отсоединения от сети целых кластеров можно реализовать дополнительный механизм повторного подключения к сети с поиском новых узлов, если в течение определенного времени узел не получал новых блоков.
При первичном подключении узла в сеть количество его соседей устанавливается достаточно маленьким. Шаг увеличения n+ растет с размером количества соседей и 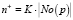 , где K – коэффициент роста. Изначально он равен Kmin, но после определенного количества блоков устанавливается в Kmax. Повышенный коэффициент при подключении позволяет узлам с высокой пропускной способностью установить большее число соединений и эффективно утилизировать имеющийся канал связи. В модельных экспериментах (описанных ниже) использовались значения Kmin = 0,1 и Kmax = 0,4, изменение коэффициента происходило через 10 временных окон.
, где K – коэффициент роста. Изначально он равен Kmin, но после определенного количества блоков устанавливается в Kmax. Повышенный коэффициент при подключении позволяет узлам с высокой пропускной способностью установить большее число соединений и эффективно утилизировать имеющийся канал связи. В модельных экспериментах (описанных ниже) использовались значения Kmin = 0,1 и Kmax = 0,4, изменение коэффициента происходило через 10 временных окон.
Новые соединения выбираются среди соседей таким образом, чтобы отдавать предпочтение наиболее эффективным узлам. Выбор производится случайно, с вероятностью, пропорциональной 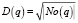 , определенной для всех известных соседей из множества C(p). Данная функция может иметь разное определение, но главное, чтобы она монотонно возрастала с числом соединений узла. При этом, однако, нельзя отдавать абсолютное предпочтение узлам с большим количеством связей, так как в этом случае будут образовываться кластеры эффективных узлов, а передача данных менее эффективным узлам будет затруднена.
, определенной для всех известных соседей из множества C(p). Данная функция может иметь разное определение, но главное, чтобы она монотонно возрастала с числом соединений узла. При этом, однако, нельзя отдавать абсолютное предпочтение узлам с большим количеством связей, так как в этом случае будут образовываться кластеры эффективных узлов, а передача данных менее эффективным узлам будет затруднена.
Количество соединений с соседями, которое необходимо закрыть, определяется формулой
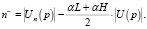 (2)
(2)
Неиспользуемые соединения, которые должны остаться после закрытия лишних, выбираются с вероятностью пропорциональной уже рассмотренной выше функции D(p), зависящей от количества используемых в настоящий момент связей. Остальные неиспользуемые соединения должны быть завершены (закрыты).
Планирование передачи данных
Поскольку структура сети определяется количеством использованных соединений за промежуток временного окна, то она зависит от работы планировщика, который определяет какой блок нужно отправить каким соседям. В ситуации, когда узел самостоятельно оценивает своих соседей, логичным выходом является схема передачи данных, в которой узел сам является инициатором отправки нужного блока другому узлу (push-based подход). Это позволяет обеспечить минимальные задержки при доставке нового блока данных, но может в некоторых случаях приводить к повторной передаче блока.
Если у узла p есть блок c, то среди его соседей есть множество N(c, p) таких узлов, у которых этого блока еще нет. Все получаемые блоки временно сохраняются в специальном буфере для дальнейшего распространения другим узлам. Информация об имеющихся блоках постоянно обновляется и должна передаваться источникам узла. Для передачи выбирается самый новый (с наиболее поздней временной меткой) блок, для которого множество N(c, p) не пусто. Из этого множества для передачи данных выбираются узлы с вероятностью пропорционально функции D(p), отражающей эффективность узла.
Моделирование
Для исследования предложенного алгоритма была разработана натурная модель, позволяющая исследовать поведение структуры сети при изменении различных параметров. При моделировании определялись несколько классов узлов и их доля от общего числа. Узлы запускались по очереди, и им назначались случайные соседи из числа уже запущенных.
При моделировании использовались 4 класса узлов [6] при следующих параметрах модели:
- класс 1–10 % пропускная способность 5 Мбит;
- класс 2–40 % пропускная способность 1 Мбит;
- класс 3–40 % пропускная способность 0,5 Мбит;
- класс 4–10 % пропускная способность 0,1 Мбит.
Средняя пропускная способность 1,11 Мбит/с, количество узлов – 1000 штук.
Источником являлся специальный узел, генерирующий новые блоки объемом 1Мбит со скоростью 10 блоков в секунду. Источник относится к классу 1 и имеет соответствующую производительность. Размер буфера данных 50 блоков (5 секунд). Параметры алгоритма: Kmin = 0,1, Kmax = 0,4, αL = 0,1, αH = 0,3. Моделирование производилось для потока данных длиной 3000 блоков (5 минут).
Наиболее важные показатели разработанного алгоритма связаны с изменением и адаптацией структуры сети. Изменение среднего числа исходящих соединений для каждого класса за время работы сети показывает рис. 1. Хорошо видно, что основная адаптация к пропускной способности узлов происходит за 50 с. Неравномерность количества соединений узлов первого класса объясняется их небольшим количеством и случайностью их появления, обусловленной вероятностной природой алгоритма.
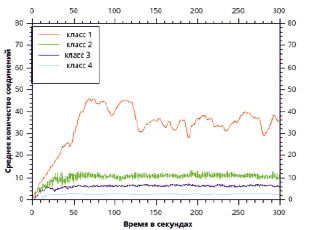
Рис. 1. Среднее количество исходящих соединений для разных классов узлов
Доля соединений между классами, а также среднее количество соединений к концу трансляции представлены в таблице. Из данной таблицы видно, что благодаря тому, что алгоритм перестроения сети предпочитает узлы с большим числом соединений, класс 1, составляющий примерно 10 % узлов, имеет 33 % соединений с узлами того же класса. Это происходит также благодаря тому, что при планировании отправки предпочитаются узлы с большей пропускной способностью и такие соединения более стабильны. Общее среднее количество исходящих соединений 11,65.
Доля исходящих соединений ( %) между классами
|
К классу 1 |
К классу 2 |
К классу 3 |
К классу 4 |
Среднее количество |
|
|
От класса 1 |
33,5 |
41,7 |
21,6 |
3,2 |
38,7 |
|
От класса 2 |
25,8 |
40,4 |
29,2 |
4,6 |
11,3 |
|
От класса 3 |
19,6 |
35,7 |
36,7 |
8,0 |
7,6 |
|
От класса 4 |
19,7 |
34,5 |
38,2 |
7,6 |
2,2 |
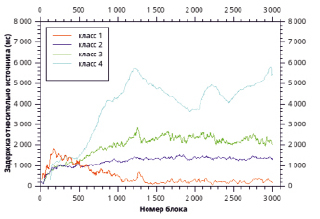
Рис. 2. Средняя задержка доставки блока
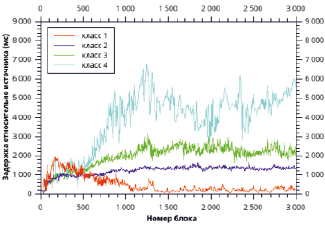
Рис. 3. Влияние переподключения узлов на задержку доставки блоков
На рис. 2 изображены графики средней задержки при доставке блоков для узлов каждого класса. Исходя из представленных данных, можно сделать вывод, что для перехода к нормальному функционированию системе требуется некоторый период адаптации, во время которого формируется ядро сети и наиболее эффективные узлы подключаются к источнику. Затем структура сети оптимизируется и минимальную задержку доставки имеют узлы с максимальной производительностью. Узлы с низкой производительностью имеют минимальный приоритет, поэтому оказываются на границах сети, а также могут терять связь с остальной сетью, что вызывает их переподключения. Этим, а также малым общим количеством узлов объясняются сильные перепады во времени доставки к низкоскоростным узлам.
Для реальных пиринговых сетей характерна высокая динамичность узлов, они постоянно отключаются и подключаются. Для того чтобы смоделировать такое поведение узлы должны с определенной вероятностью закрывать все текущие соединения и подключаться к новым случайно выбранным узлам существующей сети. В моделировании такое поведение обеспечивалось случайным отключением и новым подключением существующих узлов с вероятностью 0,01. Задержки передачи данных в такой динамичной сети представлены на рис. 3.
Заключение
Представленная схема организации пиринговой сети показала свою работоспособность в ходе испытаний, а также преимущество по сравнению с неструктурированным графом узлов в гетерогенной сети. Однако требуются дальнейшие исследования для определения эффективности модели в сетях с разной пропускной способностью, сетях больших размеров, а также надежности системы при высокой динамике изменения узлов, участвующих в сети.
Работа выполнена при поддержке РФФИ, проект № 16-01-00390.
Библиографическая ссылка
Мацько И.А., Долгов В.В., Атаян А.М. ОПТИМИЗАЦИЯ СТРУКТУРЫ ПИРИНГОВОЙ СЕТИ ДЛЯ ПЕРЕДАЧИ ПОТОКОВЫХ ДАННЫХ // Современные наукоемкие технологии. 2018. № 8. С. 105-110;URL: https://top-technologies.ru/ru/article/view?id=37128 (дата обращения: 05.07.2025).



