Распознавание образов является на сегодняшний день одной из наиболее приоритетных и актуальных проблем, стоящих перед человеческим сообществом. Оно теснейшим образом связано с задачами, возникающими в процессе проектирования и разработки надежных охранных систем; с вопросами теоретической и прикладной робототехники; с проблемами эффективного управления сложными автоматизированными комплексами поиска информации и обработки информационных потоков и т.д. Принцип, лежащий в основе всех известных процедур распознавания, довольно прост: множество признаков, характеризующих исследуемый объект, сопоставляется с набором признаков, содержащихся в заранее сформированной базе. По результатам сравнения выносится суждение о возможности отнесения объекта к какой-либо из существующих категорий или указывается категория, к которой объект наиболее близок по свойствам в рамках принятой метрики. Если же большинство характеристик не имеет аналогов в базе сравнения, объект признается неидентифицированным и становится ядром новой, ранее не существовавшей, категории, если же есть основания полагать, что результаты наблюдений сомнительны или недостоверны, объект не подлежит классификации.
Однако, несмотря на простоту идеи распознавания, процесс ее реализации может оказаться весьма затруднительным. Прежде всего заметим, что при значительном объеме базы сравнений и большом числе квалифицирующих признаков у исследуемого объекта процедура распознавания, выполняемая в виде попарного сравнения каждого признака со всеми элементами базы, крайне непродуктивна ввиду значительной трудоемкости, так как по сути сводится к полному перебору всех возможных пар.
Еще одним серьезным препятствием на пути решения задачи распознавания образов является отсутствие общепринятых формализованных правил категорирования объектов и динамическая нестабильность сформированных категорий. Действительно, структура категорий или классов определяется прежде всего целями и задачами исследований, которые могут быть существенно различны. Точно так же оказываются различными, а подчас несопоставимыми опыт и интуиция исследователей, определяющих состав классов и уровень их подготовки в предметной области. Кроме того, изменение с течением времени наполнения базы сравнений и появление новых признаков у объектов, подлежащих распознаванию, будет, несомненно, изменять конфигурацию категорий, возможно вплоть до их полного переформатирования.
Перечисленные обстоятельства и сделанные замечания позволяют утверждать что, задача распознавания образов, представляет собой сложную динамическую задачу, ряд этапов решения которой на современном уровне научных представлений не может быть строго обоснован. Усилия ученых, занимающихся исследованием этой задачи, в основном сосредоточены на разработке алгоритмов, позволяющих ускорить процесс поиска решения за счет систематизации процедуры сравнений. В частности, известны работы [1–3], в которых показана возможность ускорения распознавания путем вычисления оценок условных вероятностей принадлежности объекта определенному классу, при условии, что он обладает некоторым набором признаков (так называемый Байесовский подход). Интересным представляется также опыт использования комбинаторных методов [4]. В данной работе для решения задачи распознавания предлагается алгоритм на базе аппарата кластерного анализа. В отличие от известных [5–8], этот алгоритм позволяет учитывать динамические изменения базы сравнений и потока распознаваемых образов и использовать их в ходе дальнейших исследований.
Кластером (cluster) в традиционном понимании, которое принято в настоящей статье, называется совокупность объектов (образов) {xi}, удовлетворяющих требованию 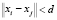 , где символ
, где символ 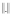 имеет смысл меры близости между объектами; d – заранее определенное граничное значение в соответствии с выбранной мерой. В данном исследовании, как и в значительном большинстве подобных работ, в качестве меры близости использована эвклидова метрика
имеет смысл меры близости между объектами; d – заранее определенное граничное значение в соответствии с выбранной мерой. В данном исследовании, как и в значительном большинстве подобных работ, в качестве меры близости использована эвклидова метрика 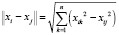 , где n – размерность пространства признаков, характеризующих распознаваемый объект.
, где n – размерность пространства признаков, характеризующих распознаваемый объект.
Применение кластерного анализа как инструмента для решения задачи распознавания образов будет тем более успешным, чем выше тенденция математических образов исследуемых объектов, как точек n-мерного пространства, к группировке около некоторых центров. Вместе с тем, как отмечалось выше, было бы нереалистичным ожидать сохранения неизменным положения этих центров с течением времени. Отсюда следует, кластеры в алгоритмах распознавания образов должны рассматриваться как подвижные динамические структуры.
Пусть имеется некоторое множество объектов X с известными свойствами, образы которых могут быть заданы точками в пространстве Rn. В дальнейшем будем называть это множество обучающей выборкой. Разобьем ее на m непересекающихся подмножеств-кластеров 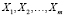 , так, чтобы
, так, чтобы 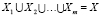 , а
, а 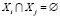 . Для
. Для 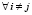 эта операция, представляющая собой первый этап кластерного анализа, является крайне неопределенной и слабо формализованной. Геометрия, размеры кластера, численный состав входящих в него элементов, критерии сходства между ними – все эти характеристики определяются содержанием и особенностями конкретной задачи, и их выбор практически целиком зависит от чисто субъективных факторов: профессиональной квалификации и интуиции исследователя.
эта операция, представляющая собой первый этап кластерного анализа, является крайне неопределенной и слабо формализованной. Геометрия, размеры кластера, численный состав входящих в него элементов, критерии сходства между ними – все эти характеристики определяются содержанием и особенностями конкретной задачи, и их выбор практически целиком зависит от чисто субъективных факторов: профессиональной квалификации и интуиции исследователя.
В данной работе мы остановили свой выбор на сферической форме кластеров. Сложность математического описания сферы, как геометрического тела, мало зависит от размерности пространства. И, поскольку число квалифицирующих признаков в задаче распознавания образов может быть достаточно большим, задание кластеров в форме сфероидов обеспечит простоту представления и интерпретации результатов.
Для построения кластерных сфероидов необходимо все классифицирующие признаки привести к единым безразмерным единицам. С этой целью, путем анализа априорной информации и материалов обучающей выборки, установим точную верхнюю xjsup и точную нижнюю xjinf грани по каждому из n признаков в проводимом исследовании и выполним переход к безразмерным переменным 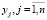 по формуле
по формуле
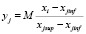 , (1)
, (1)
где M – масштабирующий множитель, выбираемый из соображений удобства представления данных. Заметим, xjsup и xjinf не обязательно должны совпадать с наибольшим и наименьшим значением классифицирующих признаков элементов исходной обучающей выборки.
На множестве элементов {yj} модифицированной обучающей выборки Y выделяем подмножество образов, образующих более или менее тесную группировку, и строим первый кластерный сфероид B1(r) с центром в точке 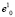 , которая расположена в непосредственной близости от геометрического центра группировки. (Причины отсутствия необходимости указаний точного положения геометрического центра группировки будут подробнее изложены ниже.) Точку
, которая расположена в непосредственной близости от геометрического центра группировки. (Причины отсутствия необходимости указаний точного положения геометрического центра группировки будут подробнее изложены ниже.) Точку 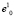 назовем начальной базовой точкой; верхний индекс указывает номер кластера, а нижний индекс – номер точки.
назовем начальной базовой точкой; верхний индекс указывает номер кластера, а нижний индекс – номер точки.
Радиус сфероида r определяется сообразно целям исследования и особенностям группировки элементов обучающей выборки. Формализованные рекомендации по его выбору до настоящего времени не разработаны. Таким образом, в состав кластера 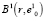 входят элементы модифицированной обучающей выборки Y, удовлетворяющие условию
входят элементы модифицированной обучающей выборки Y, удовлетворяющие условию 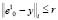 .
.
Положение полученного кластера можно и нужно уточнить, поскольку геометрический центр области, занимаемый исследуемым подмножеством обучающей выборки, как правило, не совпадает с центром тяжести группировки. С этой целью находится центр тяжести совокупности элементов, находящихся в границах сфероида 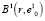 , по формуле
, по формуле
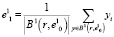 , (2)
, (2)
где 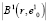 – мощность подмножества элементов в составе сфероида
– мощность подмножества элементов в составе сфероида 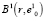 .
.
Точка 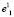 будет первой базовой точкой и геометрическим центром сфероида
будет первой базовой точкой и геометрическим центром сфероида 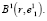 В результате этих действий в
В результате этих действий в 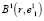 появляются элементы, которых не было
появляются элементы, которых не было 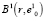 , а часть элементов, входивших в состав
, а часть элементов, входивших в состав 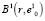 , будет потеряна. Очевидно, что и в сфероиде
, будет потеряна. Очевидно, что и в сфероиде 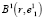 геометрический центр не будет совпадать с центром тяжести, поэтому в том же порядке находим координаты второй базовой точки
геометрический центр не будет совпадать с центром тяжести, поэтому в том же порядке находим координаты второй базовой точки 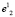 , являющейся геометрическим центром сфероида
, являющейся геометрическим центром сфероида 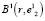 и т.д. Последовательность точек
и т.д. Последовательность точек 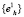 сходится, как ограниченная последовательность определенная на компакте, а значит, за конечное число шагов достигается выполнение условия
сходится, как ограниченная последовательность определенная на компакте, а значит, за конечное число шагов достигается выполнение условия 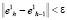 , где ε – любое заданное наперед положительное число, определяющее желаемую точность итерационной процедуры. Именно по этой причине положение начальной базовой точки
, где ε – любое заданное наперед положительное число, определяющее желаемую точность итерационной процедуры. Именно по этой причине положение начальной базовой точки 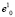 принципиального значения не имеет.
принципиального значения не имеет.
В ходе практической реализации описанного алгоритма может выясниться, что радиус сферической оболочки кластера выбран неудачно и часть элементов группировки в состав кластера 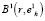 не вошло и это явно противоречит содержательному смыслу задачи. В этом случае следует увеличить размеры сфероида
не вошло и это явно противоречит содержательному смыслу задачи. В этом случае следует увеличить размеры сфероида 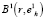 так, чтобы самый удаленный от базовой точки
так, чтобы самый удаленный от базовой точки 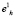 объект, из тех, что должны стать элементами кластера, попал на границу нового расширенного сфероида. Обозначим множество объектов модифицированной обучающей выборки, которые необходимо дополнительно внедрить в кластер B1, через
объект, из тех, что должны стать элементами кластера, попал на границу нового расширенного сфероида. Обозначим множество объектов модифицированной обучающей выборки, которые необходимо дополнительно внедрить в кластер B1, через 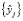 , и найдем величину
, и найдем величину
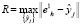 , (3)
, (3)
которая и будет определять радиус искомого кластерного сфероида 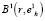 с центром в базовой точке
с центром в базовой точке 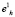 . Приращение радиуса при этом составит Δr = R – r.
. Приращение радиуса при этом составит Δr = R – r.
Естественно, что после изменения радиуса и добавления в его состав новых элементов, центр тяжести кластера сместится относительно геометрического центра точки 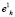 . Это смещение легко устраняется с помощью описанной выше итеративной процедуры. Это явление будет иметь место и тогда, когда формирование кластера на базе исходной обучающей выборки завершится и система начнет работать в режиме распознавания образов, обрабатывая поток объектов, поступающих на ее вход. Поэтому, если систему предполагается использовать как динамическую самообучающуюся структуру, необходимо осуществлять коррекцию положения и размеров кластерных сфероидов постоянно в течение всего периода эксплуатации. Заметим, однако, что по мере наполнения кластеров, смещение центра тяжести при поступлении новых объектов становится все менее и менее значительным. И в тех случаях, когда оно не выходит за границы ε-окрестности, корректирующее воздействие перестает быть обязательным.
. Это смещение легко устраняется с помощью описанной выше итеративной процедуры. Это явление будет иметь место и тогда, когда формирование кластера на базе исходной обучающей выборки завершится и система начнет работать в режиме распознавания образов, обрабатывая поток объектов, поступающих на ее вход. Поэтому, если систему предполагается использовать как динамическую самообучающуюся структуру, необходимо осуществлять коррекцию положения и размеров кластерных сфероидов постоянно в течение всего периода эксплуатации. Заметим, однако, что по мере наполнения кластеров, смещение центра тяжести при поступлении новых объектов становится все менее и менее значительным. И в тех случаях, когда оно не выходит за границы ε-окрестности, корректирующее воздействие перестает быть обязательным.
Классическая постановка задачи кластерного анализа предусматривает продолжение процесса построения новых кластеров вплоть до полного исчерпания элементов исходной обучающей выборки. Однако на практике это не всегда осуществимо, поскольку в исходной базе объектов могут найти такие, образы которых не могут быть отнесены ни к одному из сформированных кластеров. Как правило, это объекты, часть признаков которых лежат в непосредственной близости от точек верхних или нижних граней множества X по соответствующим координатам. Эти объекты остаются внекластерными, но, как отмечалось выше, при определенных обстоятельствах могут стать центрами новых кластерных образований.
Особо следует обратить внимание на недопустимость наличия общих элементов у различных кластеров. Если же в ходе кластеризации обнаружится факт пересечения хотя бы пары кластеров, то это является неоспоримым свидетельством слабо выраженной тенденции группировки в обучающей выборке и неэффективности аппарата кластерного анализа применительно к данному множеству.
Рассмотрим действие описанного алгоритма на примере достаточно представительной обучающей выборки, элементами которой являются города Российской Федерации. В качестве их характеризующих признаков выберем численный состав населения этих городов, x, и территорию ими занимаемую, S. Фрагмент этой выборки представлен в табл. 1.
Для реализации алгоритма необходимо установить положение точных нижних и точных верхних граней по каждому признаку. Для признака x – население в качестве точной нижней грани целесообразно принять xjinf = 10000, поскольку поселения, число жителей в которых не превосходит 10000, не имеют в Российской Федерации статуса города.
В качестве точной верхней границы следует, по нашему мнению, xjsub = 5000000, так как городов с населением более 5000000 человек в Российской Федерации только 2 и они имеют особый правовой статус, структуру и систему управления.
Таблица 1
Cписок городов России с территорией и населением
|
№ п/п |
Город |
Население, чел. |
Площадь, км2 |
|
1 |
Новосибирск |
1 602 915 |
506,67 |
|
2 |
Уфа |
1 115 560 |
707 |
|
3 |
Орск |
230 414 |
621,33 |
|
4 |
Казань |
1 231 878 |
614,16 |
|
5 |
Волжский |
326 055 |
229,12 |
|
6 |
Омск |
1 178 391 |
566,9 |
|
7 |
Самара |
1 169 719 |
541,382 |
|
8 |
Ростов-на-Дону |
1 125 299 |
348,5 |
|
.. |
… |
… |
… |
|
137 |
Дербент |
123 162 |
69,63 |
Таблица 2
Множество элементов обучающей выборки, приведенных к безразмерным переменным
|
№ п/п |
Город |
y |
V |
|
1 |
Новосибирск |
41,9 |
46,1 |
|
2 |
Уфа |
32,1 |
60,4 |
|
3 |
Орск |
14,4 |
54,3 |
|
4 |
Казань |
34,4 |
53,8 |
|
5 |
Волжский |
16,3 |
26,3 |
|
6 |
Омск |
33,4 |
50,4 |
|
7 |
Самара |
33,2 |
48,6 |
|
8 |
Ростов-на-Дону |
32,3 |
34,8 |
|
.. |
… |
… |
… |
|
137 |
Дербент |
12,2 |
14,9 |
Пример
Что касается площади, то по аналогичным соображениям в качестве точной нижней грани Sjinf следует принять 1 км2, а в качестве точной верхней грани Sjsup величину равную 1400 км2, поскольку город Санкт-Петербург, население которого составляет 5,2 млн человек, имеет в настоящее время именно такую площадь. Используя формулу (1), приведем значения признаков x и S к безразмерным переменным y и V. В табл. 2 представлен фрагмент обучающей выборки, элементы которой пересчитаны по формуле (1).
На рис. 1 множество элементов обучающей выборки, приведенных к безразмерным переменным, представлено точками плоскости в координатах y – V с масштабирующим множителем М = 100. ε = 0,5, где ε – наперед заданное положительное число, определяющее желаемую точность итерационной процедуры.
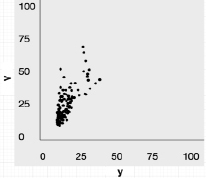
Рис. 1. Множество элементов обучающей выборки в безразмерных координатах
Для начала процедуры кластеризации было принято решение сформировать три исходных кластера, границы которых и положения их геометрических центров представлены в табл. 3. Предложенное разделение весьма условно и служит только для того, чтобы зафиксировать начальное положение для запуска изложенного выше алгоритма динамической кластеризации. Процесс эволюции кластерных сфероидов, как результат действия этого алгоритма, можно проследить по материалам табл. 4. Из данных этой таблицы видно, что для определения окончательного первого кластера оказалось достаточно двух итераций, при этом радиус кластерного сфероида сохранил свое первоначальное значение. Это вполне ожидаемый факт, который объясняется тем, что группировка объектов выборки в области первого кластера (условно малых городов) выражена наиболее отчетливо (см. также рис. 1).
Таблица 3
Начальные границы кластеров, заданные пользователем
|
№ кластера |
Границы населения [xjinf, xjsup] |
Границы площади [Sjinf, Sjsup] |
|
1 |
[10000, 500000] |
[1, 150] |
|
2 |
[500001, 1000000] |
[151, 700] |
|
3 |
[1000001, 1700000] |
[701, 1000] |
|
№ кластера |
Центр кластера [население, площадь] |
Радиус r |
|
1 |
[254999, 75,5] |
7,2 |
|
2 |
[750000, 425,5] |
20,2 |
|
3 |
[1350000, 850,5] |
12,7 |
Процесс преобразования второго и третьего кластеров потребовал 5–6 итераций соответственно и сопровождался более значительными изменениями, поскольку они затронули не только положение центров кластерных сфероидов, но и величины их радиусов. Особенно заметно это проявляется для второго кластера, где радиус, по сравнению с исходным, изменился более чем в 3 раза, что было вызвано необходимостью устранения возможности пересечения кластеров. Заметим также, что изменение положения центров кластерных образований устойчиво направлено в сторону меньших значений характеризующих признаков, т.е. в область более выраженной плотности группировки.
Промежуточные этапы и конечный результат расчетов, выполненных в соответствии с разработанным алгоритмом, подробно проиллюстрирован на рис. 2. В левой части рисунка представлена вся последовательность преобразований кластерных сфероидов. Пунктирными окружностями изображены границы промежуточных кластеров (см. также рис. 2), а сплошными – их конечная позиция, которую можно считать жестко зафиксированной для выбранного показателя точности вычислений ε и заданного объема обучающей выборки.
Таблица 4
Этапы преобразованных кластеров
|
№ п/п |
Центр кластера [население, площадь] |
Радиус r |
|
|
1 |
|||
|
1 |
[220698, 102,5] |
7,2 |
|
|
2 |
[227734, 108,1] |
7,2 |
|
|
2 |
|||
|
1 |
[567468, 334,4] |
10,2 |
|
|
2 |
[461127, 316,1] |
8,2 |
|
|
3 |
[442760, 305,5] |
7,2 |
|
|
4 |
[439437, 301,9] |
8,2 |
|
|
5 |
[443997, 293,5] |
6,2 |
|
|
3 |
|||
|
1 |
[1059716, 788,7] |
29,7 |
|
|
2 |
[978274, 557,8] |
13,7 |
|
|
3 |
[1024047, 514,5] |
11,7 |
|
|
4 |
[1073611, 485,8] |
10,7 |
|
|
5 |
[1117677, 480,0] |
11,7 |
|
|
6 |
[1117677, 480,0] |
10,7 |
|
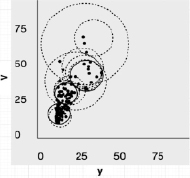
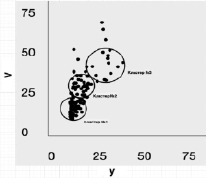
Рис. 2. Этапы и конечный результат расчетов, выполненных в соответствии с разработанным алгоритмом
Материалы табл. 4 и рис. 2 дают основание указать важное свойство алгоритма динамической кластеризации, а именно его самоорганизуемость. Действительно, нельзя не обратить внимание на то, что размеры радиуса второго кластера (городов с условно средним числом жителей) существенно уменьшились, а положение центра сместилось в сторону меньших значений по сравнению с исходным. В то же время границы кластера крупных городов стали охватывать часть городов, которые формально не относятся к числу мегаполисов. Это свидетельствует о том, что, во-первых, размеры кластерных сфероидов не следует устанавливать, ориентируясь на «круглые» числа, а во-вторых, в рамках обучающей выборки с данными характеризующими признаками (население, площадь) города с числом жителей 800–900 тыс. человек ближе по своей структуре к мегаполисам, нежели к городам с населением 500 тыс. человек.
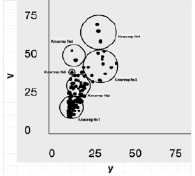
Рис. 3. Этапы и повторный результат расчетов, выполненных в соответствии с разработанным алгоритмом
Из рассмотрения правой части рис. 2 видно, что несколько объектов сформированных кластеров и возможность их внедрения в один из созданных кластеров путем увеличения радиуса отсутствует. Для этих элементов обучающей выборки алгоритм запускается повторно, результатом чего становится появление трех новых кластерных образований (рис. 3), число элементов в которых значительно меньше, чем в первых трех кластерах. Это не снижает ценность полученных результатов и не дискредитирует разработанный алгоритм, поскольку по мере пополнения обучающей выборки и естественных изменений входящих в нее объектов структура кластерного сообщества должна и будет меняться, что и составляет главный содержательный смысл идеи динамической кластеризации. В табл. 5 приведен результат реализации разработанного алгоритма динамической кластеризации в данном примере (список городов с определенными номерами кластеров).
Таблица 5
Список городов с определенными номерами кластеров
|
№ п/п |
Город |
Население, чел. |
Площадь, км2 |
№ кластер |
|
1 |
Новосибирск |
1 602 915 |
506,67 |
3 |
|
2 |
Уфа |
1 115 560 |
707 |
4 |
|
3 |
Орск |
230 414 |
621,33 |
5 |
|
4 |
Казань |
1 231 878 |
614,16 |
3 |
|
5 |
Волжский |
326 055 |
229,12 |
2 |
|
6 |
Омск |
1 178 391 |
566,9 |
3 |
|
7 |
Самара |
1 169 719 |
541,382 |
3 |
|
8 |
Ростов-на-Дону |
1 125 299 |
348,5 |
3 |
|
.. |
… |
… |
… |
|
|
137 |
Дербент |
123 162 |
69,63 |
1 |
Выводы
1. Для решения задачи распознавания образов разработана математическая модель самоорганизующейся системы кластеров.
2. Показано, что кластеры являются динамическими образованиями, изменяющимися под воздействием потока распознаваемых образов.
3. Разработан и апробирован алгоритм динамической кластеризации, действующий на заданном множестве характеризующих признаков определенной предметной области.
4. Для практической реализации алгоритма разработан специализированный программный комплекс.
5. Заложены основы эволюционного формирования кластерной модели, позволяющей использовать ее для решения задач эффективного управления.
Библиографическая ссылка
Печеный Е.А., Аль-Хашеди А.А., Нуриев Н.К. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИЧЕСКОЙ КЛАСТЕРИЗАЦИИ В ЗАДАЧАХ РАСПОЗНАВАНИЯ ОБРАЗОВ // Современные наукоемкие технологии. 2018. № 5. С. 124-130;URL: https://top-technologies.ru/ru/article/view?id=37003 (дата обращения: 09.07.2025).



