Задача распознавания образов по своей сути не нова и возникает в самых разнообразных направлениях исследований, начиная от прикладных задач в области безопасности и оцифровки аналоговых сигналов до задач теории оптимального управления и дифференциальных игр. Наибольшее развитие и совершенствование методов решения данных задач наблюдается в современности. Связано это прежде всего с необходимостью снятия возникающих огромных информационных нагрузок с человека и необходимостью использовать одновременно мышление и восприятие, свойственное распознаванию. Все эти задачи имеют ярко выраженный междисциплинарный характер и являются основой развития нового поколения технических систем распознавания, носящих сугубо узконаправленный и практический характер в различных направлениях, включая медицину и создание искусственного интеллекта. Одним из самых ранних направлений исследований было оптическое распознавание символов (Optical Character Recognition, OCR).
Анализ методов определения Хаусдорфова расстояния
Среди большого количества работ, посвященных данной тематике, следует выделить обзорную работу [1]. В ней затрагивают как теоретические аспекты, так и аспекты практического плана с точки зрения разработки алгоритмов. Еще в 1990-х гг. написана работы П. Грубера [2] освещающая различные грани аппроксимации выпуклых тел и дальнейшее развитие и исследование смежных с данной темой вопросов. Автор подчеркивает, что наряду с развитием совершенной формы классических подходов появились выдающиеся результаты об аттрактивных множествах.
Хаусдорфовой метрикой [3, 4] называют расстояние h на некотором заданном множестве D между его подмножествами X, Y, где
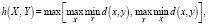
где d(x, y) – расстояние между элементами подмножеств заданного множества.
На сегодняшний день существует большое количество работ так или иначе связанных с метрикой Хаусдорфа, реализацией алгоритмов решения различных задач с ее применением и оптимизации существующих алгоритмов. Однако в литературе слабо описаны алгоритмы низкоуровневой оптимизации, применительно к решению задач такого класса. Именно по этой причине в настоящей работе автор останавливается на данном вопросе.
Определение метрического пространства в работе [5] сформулировано для выпуклых неограниченных замкнутых подмножеств Банахового с использованием метрики Хаусдорфа и установили отличия свойств выпуклых с данной метрикой от свойств метрического пространства. Исследования в работе [6] привели к важному утверждению, что не каждый объект в метрическом пространстве может быть аппроксимирован обобщенными многогранниками и в связи с этим ввели понятие обобщенного многогранника и критерии аппроксимации. Показали, что для аппроксимации равномерная непрерывность опорной функции является необходимым и достаточным условием.
Другая не менее важная задача о минимизации метрики Хаусдорфова между двумя выпуклыми многоугольниками решалась в работе [7]. Авторы рассматривают два многоугольника: один являлся неподвижным, а другой мог изменять свое местоположение на плоскости (вращение или параллельный перенос).
Ушаков и Лебедев [8] разработали и апробировали итерационные алгоритмы пошагового сдвига и вращения, гарантирующие уменьшение Хаусдорфова расстояния между подвижным и неподвижным объектами с использованием дифференциальных свойств функции евклидова расстояния до выпуклого множества и геометрических свойств чебышевского центра компактного множества, и доказали теоремы о корректности разработанных алгоритмов для широкого класса случаев. Многократный запуск алгоритма позволяет выбрать наилучший из вариантов.
В работах А.Б. Куржанского [9] и Ф.Л. Черноусько [10] используют в работах аппроксимацию эллипсоидами и параллелепипедами при решении задач оптимального управления множества достижимости динамических систем. В данном случае критерием оптимальности является расстояние Хаусдорфа.
По причине нарастания информатизации пространства и повышения интенсивности применения вычислительной техники не только обычными людьми для бытовых нужд, но и узкими специалистами в своей работе, растет потребность в алгоритмах и их оптимизации – как на алгоритмическом уровне, так и с применением новейших параллельных технологий. Еще одним не менее важным направлением исследовательской работы считается создание новых оптимизационных алгоритмов. Чтобы сравнивать создаваемые алгоритмы с уже имеющимися, разработчики применяют метрики Хаусдорфа в роли критерия их оптимальности. Еще одним серьезным минусом генетического алгоритма можно назвать чрезмерную вычислительную сложность. Потребуется обучить огромное число суррогатных моделей и выполнить глобальный поиск максимума вероятности улучшения. Перечисленные шаги потребуют значительных временных затрат. Невзирая на вышеуказанные минусы алгоритма, его предназначением являются сложные целевые функции. При этом с вычислительной точки зрения, чем дольше длится вычисление, тем меньше будет относительное время работы алгоритма.
Методы низкоуровневой оптимизации
Отсюда следует, что применение оптимизации на базе метрики Хаусдорфа станет возможным, если привести структуры начальных данных или в векторный вид, или в матричный, в соответствии с подобранными критериями. Представление первоначальных данных в подобном формате дает возможность пользоваться матричным алгоритмом оптимизации, реализованным, к примеру, в MATLAB, либо специализированными алгоритмами записи и сохранения алгоритмов в памяти ЭВМ, а также пользоваться низкоуровневой оптимизацией, рассмотренной в работе [11].
Наиболее детальное описание современных алгоритмов представлено в работе [12]. Авторы сделали подробное описание алгоритмов распознавания многоугольников с установленным порогом для вычисления расстояния. Было продемонстрировано, что созданный алгоритм находит решение задачи за временной период порядка (m×n), при этом обычным алгоритмам необходимо (m×n)log(m×n). Авторы представили подробное описание алгоритмов для геометрических объектов, таких как цепочка, цикл, ломаные линии и многоугольники. В работе [12] продемонстрировано, что трудоемкость вычислений увеличивается в последующем порядке: вначале цепочки, далее циклы, потом ломаные и в конечном итоге многоугольники. Они разработали алгоритм для проверки усиленного неравенства для n-угольников множества Y и m-угольников множества X, с линейной зависимостью от этих величин.
Общеизвестно [11], что при обработке огромных массивов данных появляется потребность в ускорении вычислительного процесса. Выполним краткий анализ используемых сегодня технологий распараллеливания. Бурный рост параллельного программирования стал причиной возникновения разнообразных технологий параллельного обрабатывания данных. В числе первых кластерных технологий появилась технология MPI (от англ. Message Passing Interface, в переводе – интерфейс передачи сообщений). В дальнейшем на базе MPI был разработан GRID, выполняющий роль средства группового использования вычислительных мощностей с помощью сети Интернет. Одновременно с совершенствованием кластерных и узловых технологий развивались и методики распараллеливания внутри одного вычислителя. Вначале была разработана технология поддержки многопоточности в рамках одной программы. После возникновения многоядерных и мультипроцессорных систем данная технология получила второе рождение, и сегодня нередко используется в различных приложениях.
Одной из самых известных и востребованных технологий стала OpenMP, базирующаяся на многопоточности. Технологии распараллеливания вычислений, без сомнений, дают превосходную возможность повысить скорость вычислений, однако они обладают определенными недостатками, наиболее значимым из которых можно назвать фактическую неосуществимость полного распараллеливания алгоритма и выхода на линейную зависимость увеличения производительности от количества процессоров.
В 1990-х гг. A.Г. Гофман внес предложение по синхронной работе с оперативной памятью, притом с блоками, расположенными в разных сегментах. Однако, если принять во внимание специфику архитектуры нынешних компьютеров, становится ясно, что она нивелирует любой временной выигрыш, полученный при одновременном исполнении арифметических операций в алгоритме. Данное обстоятельство сопряжено с тем, что время доступа к ячейкам памяти, расположенным на определенной дистанции друг от друга, превышающей размер процессорной КЭШ-линии (а в особенности в различных сегментах памяти) порождает Cache Miss (КЭШ-промахи). В результате появляется задержка в работе системного микропроцессора в размере сотен тактов, при этом для выполнения простых арифметических действий, таких как складывание, вычитание, перемножение и деление (требует больше всего времени из перечисленных), необходимо лишь несколько десятков тактов [11]. Если появится потребность, можно прибегнуть к последовательному перебору линий данных в обоих направлениях.
Чтобы распараллелить вычисления с применением кластерного подхода и подключением библиотеки MPI, необходимо особое программное обеспечение, инсталлированное на каждый узел кластера, а кроме того, огромное число компьютеров, исполняющих функцию этих узлов. Помимо этого, при создании параллельной реализации алгоритма необходимо свести к минимуму информационный обмен между узлами, поскольку это играет роль «бутылочного горлышка» в рассматриваемой системе.
Самой перспективной и занимательной из вышеупомянутых технологий можно считать мелкозернистую сборку вычислений, изобретенную с целью поддержки параллельной реализации крупномасштабных численных моделей. Вместе с мелкозернистой сборкой и трехмерной декомпозицией расчетной области происходит распределение итоговых частей между кластерными узлами. Но, увы, мелкозернистая сборка обеспечивает прирост производительности лишь на довольно крупномасштабных моделях, обрабатывающих огромные массивы данных и осуществляющих огромное число вычислительных операций. Кроме того, подобная реализация обеспечивает значительное увеличение быстродействия лишь в случае наличия слабой связи по данным между элементами расчетной области.
Результаты и их анализ
Тем не менее использование низкоуровневой оптимизации доступно лишь тем, кто разбирается в механизме исполнения команд на нынешних микропроцессорах. Воспользовавшись этими сведениями, можно добиться значительного ускорения выполнения процедуры (на десятки процентов). Низкоуровневая оптимизация потребления сверхоперативной памяти состояла в «комфортном» для вычислителя расположении ряда ключевых массивов данных, а это в свою очередь повышало быстродействие минимум на 15 %, исходя из величины массивов. Такое размещение для трехмерных массивов показано на рис. 1.
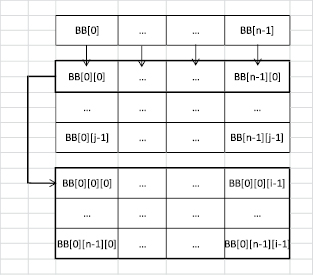
Рис. 1. Размещение в памяти 3D массива для низкоуровневой оптимизации
Использование низкоуровневой оптимизации приводит к существенному ускорению процесса вычислений. В качестве базы для оценки эффективности низкоуровневой оптимизации был использован распараллеленный, но не оптимизированный на низком уровне код. На рис. 2 показано ускорение вычислений в результате оптимизации при распараллеленном коде. Как видно из рисунка, оптимизация позволяет увеличить скорость вычислений на 41 %.
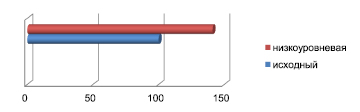
Рис. 2. Увеличение быстродействия вследствие низкоуровневой оптимизации
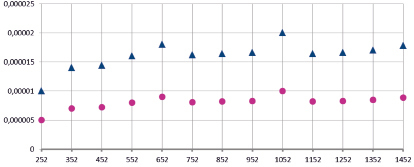
Рис. 3. Рост скорости при эффективном использовании низкоуровневой оптимизации
На рис. 3 показана зависимость времени выполнения кода, ортонормированная на объем данных. На графике видно, что на отдельных размерностях сетки наблюдается серьезное замедление вычислительного процесса, что сопряжено с недостаточно рациональным использованием cache-памяти вычислителя. Проведение низкоуровневой оптимизации увеличит рациональность использования cache-памяти, а благодаря этому возрастет и вычислительная скорость на 40 %, как демонстрирует розовая кривая.
Заключение
Подытоживая, стоит отметить, что увеличение быстродействия достигнуто благодаря росту рациональности использования КЭШ-памяти вычислителя. При добавлении распараллеливания на многоядерных машинах наблюдается дополнительный рост вычислительной скорости.
Библиографическая ссылка
Данилов Д.И. ОЦЕНКА ЭФФЕКТИВНОСТИ ИСПОЛЬЗОВАНИЯ НИЗКОУРОВНЕВОЙ ОПТИМИЗАЦИИ АЛГОРИТМА ОПРЕДЕЛЕНИЯ ХАУСДОРФОВА РАССТОЯНИЯ ДЛЯ ВЫПУКЛЫХ (ИЛИ НЕВЫПУКЛЫХ) МНОГОУГОЛЬНИКОВ // Современные наукоемкие технологии. 2018. № 3. С. 30-34;URL: https://top-technologies.ru/ru/article/view?id=36932 (дата обращения: 15.02.2026).
DOI: https://doi.org/10.17513/snt.36932



