В настоящее время в отраслях тяжёлого, атомного и энергетического машиностроения в России получают всё большее распространение современные технологии 3D-проектирования и моделирования. Однако не все потенциальные возможности таких технологий реализуются, в частности, в сфере котлостроения. Несмотря на то, что современные программные (вычислительные) комплексы позволяют проводить расчёты высокой сложности практически любых узлов и конструкций, такие расчёты не включены в нормативные документы, а анализ результатов оставлен в зоне ответственности проектных организаций. Регламент Таможенного союза [1] разрешает проектным организациям проводить использование численных методов наряду с отраслевыми нормами, но разработка комплексных методик анализа конструкций возлагается на исполнителя проекта. В данной статье представлен обзор методик и методов создания конечно-элементных моделей и достижения технических результатов в области анализа прочности конструкций применительно к энергетическим котлам.
Специалисты-расчётчики, работающие в области тяжёлого и энергетического машиностроения, сталкиваются с необходимостью проведения анализа сложных конструкций, состоящих из комплекса разнородных узлов. Такие системы включают тонкостенные и толстостенные сосуды, трубопроводы, газоходы, различные металлоконструкции и каркасные узлы, цельносварные трубные панели, трубные поверхности нагрева и другие конструкции. Разнородные узлы завязаны в единую конструкцию, поэтому совместно деформируются с передачей в связях различных наборов усилий. Нормативные методы часто не позволяют достаточно точно учесть все эти взаимодействия. Напротив, современные вычислительные системы обеспечивают возможность уточнённого анализа сложных систем с учётом связей и взаимные влияния элементов конструкций. Здесь надо отметить, что погрешность результата и трудоёмкость расчёта и моделирования конструкций численными методами определяются используемой методикой и эффективностью моделей. Поэтому одной из основных задач специалиста-расчётчика, занятого моделированием конструкций, является построение эффективных моделей. Критерием эффективности здесь служит отношение времени выполнения задачи и точности полученных результатов.
Рассмотрим на примере котельных конструкций ряд методик, позволяющих достигнуть достаточного по точности технического результата при относительно малой трудоёмкости моделирования и малом времени вычислений. Это следующие методики:
1) построение оптимальных геометрических моделей – позволяет существенно снизить трудоёмкость построения моделей и время вычислений;
2) методика субмоделирования (Submodeling) – позволяет повысить точность результатов расчёта для всех узлов сложных моделей;
3) методика субструктурирования (Substructuring) – позволяет снизить машинное время расчёта и уровень требований к расчётным станциям.
Построение оптимальных геометрических моделей
Оптимальная геометрическая модель здесь – модель, достаточно точно отражающая геометрию и особенности конструкции и позволяющая при возможно малом количестве конечных элементов обеспечить требуемую точность результатов моделирования при малых затратах времени на создание модели и дальнейших вычислений.
При моделировании таких сложных систем, как энергетический котёл, состоящий из цельносварных газоплотных трубных панелей, опорных металлоконструкций, поверхностей нагрева и трубопроводов, применение твердотельного моделирования приводит к большой трудоёмкости создания модели. Но главное – весьма большое число конечных элементов модели приводит к высоким требованиям по мощности компьютера (нужно использовать либо специальные вычислительные станции, либо вычислительные кластеры) и длительным вычислительным операциям.
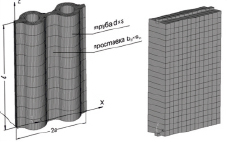
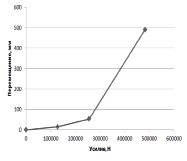
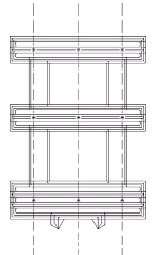
В общемировой практике принято моделировать сложные котельные конструкции при помощи балочных (BEAM), оболочечных (SHELL) и трубных (PIPE) конечных элементов [2]. Основные металлоконструкции моделировать балочными элементами «как есть», вспомогательные – балочными элементами эквивалентных сечений, а наиболее сложные для моделирования мембранные экраны описывать с помощью оболочечных элементов со специальным образом рассчитанными толщиной и механическими свойствами (см. рис. 1, а) [3–5]. Поверхности нагрева моделировать трёхмерными твердотельными элементами в случае, когда можно ограничиться рассмотрением отдельных узлов или элементов [6]. В остальных случаях поверхности нагрева моделируются трубными элементами «как есть» или заменяются элементами сосредоточенной массы, если поведением змеевиков можно пренебречь (см. рис. 1, в). Кроме того, такие сложные конструкции, как энергетический котёл, имеют специфические элементы, которые моделируются особым образом в каждом отдельном случае. Так, например, «антисейсмические упоры» – энергопоглощающие упруго-пластичные элементы, имеющие нелинейную характеристику жесткости, моделируются с помощью комбинированных (COMBINE) элементов (см. рис. 1, б). Узлы крепления моделируются с помощью задания уравнений связи (СР, СЕ) (см. рис. 1, г). Построение геометрии объекта ведётся с использованием специализированных пакетов 3D-проектирования и программных модулей. Последние конструируют балочно-оболочечную геометрию по твердотельным моделям при помощи специальных инструментов. При этом пользователь задаёт элементы, которые в результате упрощения станут оболочками или стержнями.
а б

в г
Рис. 1. Моделирование элементов энергетического парового котла: а – моделирование цельносварных газоплотных экранов с помощью перехода от твердотельных моделей к оболочечно-стержневым; б – диаграмма сила – перемещение при моделировании упруго-пластических элементов с помощью элементов типа COMBINE; в – моделирование конвективного пароперегревателя с помощью элементов типа PIPE и элементами сосредоточенной массы (изображены в виде звёздочек); г – моделирование узлов крепления поясов жесткости с помощью уравнений связи
В случае если большая часть модели состоит из заменяющих структур с характеристиками, эквивалентными реальным элементам конструкций, то описанные выше инструменты упрощения оказываются непригодными, так как не существует соответствующих алгоритмов преобразования твердотельных реальных элементов в заменяющие структуры. В этом случае наиболее эффективным способом построения моделей становится создание геометрии «с нуля» в специализированных пакетах 3D-моделирования (CAD-пакетах) и экспорт модели в расчётные программы (пакеты САЕ). Тогда создаются трёхмерные ассамблеи поверхностей нулевой толщины с необходимым количеством биений, моделирующих балки, стержни и т.д.
Методика субмоделирования (Submodeling)
Методика субмоделирования применяется для уточнения результатов моделирования в определённых локальных местах модели. В этом случае моделирование сложных конструкций и анализ результатов проводится в два этапа: на первом выполняется обобщённая модель всей конструкции (структуры) и выявляются наиболее проблемные локальные зоны, например, с высокими механическими напряжениями, на втором этапе проводится субмоделирование и детальный анализ локальных зон.
Необходимо отметить, что детализация напряженно-деформированного состояния некоторых узлов невозможна без применения такой методики. Это касается в первую очередь узлов, геометрия которых подвергалась значительным упрощениям.
Примерами могут служить мембранные экраны топок энергетических котлов и опорные металлоконструкции. Модели мембранных экранов на первом – ортотропные пластины, а модели опорных металлоконструкций – стержни эквивалентных сечений.
Субмоделирование выполняется следующим образом:
1) в исходной модели выделяют область интереса, включающую конечные элементы и их узлы;
2) далее переходят к границам выделенной области, в которых происходит сопряжение с остальными частями модели;
3) далее производят сохранение координат и степеней свободы граничных узлов; в ПК ANSYS эти операции выполняются с помощью команд: NWRITE, CBDOF;
4) кроме того, если производится субмоделирование температурной задачи, необходимо произвести интерполяцию распределения температур для уточнённой модели. В ПК ANSYS для этого служат команды NWRITE (предварительно в области интереса должны быть выбраны все элементы и их узлы), BFINT;
5) далее выполняют уточнённую модель и в местах сопряжения прикладывают сохранённые ранее граничные условия. При этом существует правило: если в исходной модели существовали какие-либо граничные условия и нагрузки, захватывающие область субмоделирования, эти граничные условия должны быть заданы и в уточнённой модели.
Применение субмоделирования позволяет выполнять весьма точный анализ напряжённо-деформированного состояния локальных зон сложных конструкций. Рекомендуем применять субмоделирование только для уточнения напряжённо-деформированного состояния с наибольшими напряжениями, там, где были применены эквивалентные элементы и для получения напряжённо-деформированного состояния особых точек, анализ которых требуется отраслевым нормативом. Применять субмоделирование для сложных конструкций в целом нецелесообразно – это на порядки повышает трудоёмкость моделирования и длительность вычислительных операций, тем более, что прочность конструкции лимитируют зоны высоких напряжений, а остальные области конструкции не представляют интереса для подробного анализа. Для них не рекомендуется производить субмоделирование.
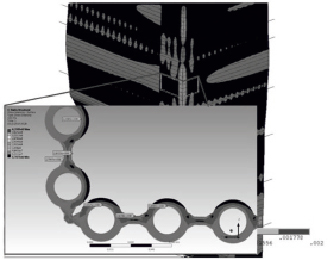
Совместное и последовательное использование построения оптимальных геометрических моделей с эквивалентными элементами и субмоделирования позволяет добиваться кратного снижения машинного времени [4]. Для примера на рис. 2, а, представлены результаты субмоделирования локальной области модели котлоагрегата.
Методика субструктурирования (Substructuring)
Методика субструктурирования применяется для анализа особо крупных структур, традиционный анализ которых требует слишком большого времени расчёта и высоких требований к вычислительным станциям. Суть метода заключается в замене некоторых блоков элементов единичными матричными элементами. Такие элементы называют суперэлементами. Работа с суперэлементами производится так же, как и с любыми другими элементами. Единственное отличие состоит в том, что предварительно производится вычисление матриц для суперэлемента.
а

б
Рис. 2. Примеры моделирования: а – использование методики субмоделирования для определения напряженного состояния цельносварных газоплотных экранов топки котла; б – использование методики субструктурирования при расчётах элементов котлов (рамкой выделены элементы, которые заменяли суперэлементами)
Субструктурирование выполняется в три этапа:
1. Этап генерации (GENARATION PASS). На этом этапе производят выделение блока элементов и их узлов для создания суперэлемента. При этом предполагается, что геометрия всей конструкции определена, построена сетка как минимум для области субструктурирования. В программном комплексе ANSYS для этапа генерации отведён специальный расчёт (ANTYPE, SUBSTR). Предварительно в местах соединения суперэлемента и других элементов модели задают мастер-узлы (команда М). Перед расчётом указывают, какие матрицы должны быть рассчитаны (матрицы жесткости, масс, демпфирования).
2. Этап использования (USE PASS). На этом этапе производят расчёты с использованием ранее сгенерированных суперэлементов. В ПК ANSYS существует специальный тип элементов, позволяющий выполнять субструктурирование – MATRIX50. Матрицы для этого элемента заполняются командами SE, SEOPT. Необходимо отметить, что на этапах генерации и использования должны быть заданы различные имена задачи (команда /FILNAME).
3. Этап расширения (EXPANSION PASS). На этом этапе производятся расчёты для степеней свободы элементов, входящих в суперэлемент. В ПК ANSYS для этого используются команды EXPASS, EXPSOL, SEEXP.
Следует отметить, что выделяют два метода выполнения субструктурирования: снизу вверх и сверху вниз. В первом случае отдельно моделируются и рассчитываются группы элементов для каждого суперэлемента, а результаты собираются вместе на этапе использования. Во втором – сразу создаётся модель всей конструкции, потом выполняется замена некоторых частей модели суперэлементами.
Метод снизу вверх более трудоёмок и применяется для расчёта особо сложных конструкций. В энергомашиностроении метод субструктурирования мы рекомендуем применять при моделировании поверхностей нагрева (блоков конвективных пароперегревателей, экономайзера). Это блоки трубчатых змеевиков, выходящих и входящих в коллекторы – трубы большего диаметра. Поверхности нагрева состоят из десятков змеевиков, поэтому прямое моделирование PIPE – элементами таких узлов приводит к кратному возрастанию времени расчёта. Количество частот и форм собственных колебаний такого узла измеряется тысячами. Соответственно, анализ динамики таких элементов требует мощных расчётных станций и длительного времени вычислений. Поэтому рекомендуем заменять поверхности нагрева суперэлементами. На рис. 2, б приведён пример замены блоков экономайзера матричными элементами.
Практика использования вышеизложенных методик позволяет сократить число конечных элементов моделей конструкций с экранами на несколько порядков, снизить трудоёмкость формирования моделей конструкций с экранами в 10–15 раз и более, а время вычислительных операций при расчете напряженно-деформированного состояния таких конструкций, как топка или конвективная шахта котла с её опорной системой, сокращается на несколько порядков. Так, число твердотельных конечных элементов, использованных в модели локального участка мембранного трубного экрана при определении перемещений, составило ~5500. Число оболочечных и стержневых элементов, использованных в модели на основе ортотропной пластины, составило 286. Таким образом, число элементов сократилось до 20 раз, а размерность модели сократилась до 100 раз в зависимости от используемых типов элементов – линейных или квадратичных.
При выполнении моделирования напряженно-деформированного состояния холодной воронки парового котла с её опорными элементами и входными размерами сечения воронки 22×16 м и высотой 21,8 м число конечных элементов экранов – наклонных фронтовых и боковых при моделировании по предложенному способу составило 285000, из которых элементов, моделирующих экраны – 190000. При этом моделирование холодной воронки с её опорной системой по предлагаемому способу проводилось на персональном компьютере с параметрами Intel Core i7-2600K CPU @ 3.4GHz, 12 ГБ ОЗУ, время расчета по одному варианту при вариантном проектировании, в том числе элементов опорных конструкций, их расположения, поперечных сечений и так далее, составляло около 10 мин. При этом выполнение субмоделирования отдельных элементов конструкций проводилось на тех же рабочих станциях. Следует отметить, что при переходе к оболочечным моделям погрешность по деформациям для сложного нагруженного состояния составляет менее 7 %. Напряжения, которые рассчитываются для эквивалентных структур, в методике не используются. Для определения напряжений используют либо аналитические выражения, либо дополнительный математический аппарат. В качестве такового, на наш взгляд, идеально подходит применение субмоделирования. В случае выполнения расчетов при твердотельном моделировании всей холодной воронки потребовалось бы использование суперкомпьютера и время вычислительных операций измерялось бы часами и десятками часов.
При выполнении моделирования напряженно-деформированного состояния перепускных труб ВЭК, ВЭК и КПП НД с коллекторами, подвесной системы, цельносварных газоплотных экранов конвективной шахты, укреплённых поясами жесткости и др. металлоконструкциями котла средней мощности число конечных элементов составило 322500, из которых элементов, моделирующих экраны – 9713, элементов, объединённых в суперэлемент – 3×62820 = 188460, элементов, заменявшихся элементами точечной массы на этапе динамического расчёта – 3×29100 = 87300. При этом время статического расчёта полной модели при включении опции учёта больших деформаций (команда NLGEOM,ON) составило 2 часа 30 минут на компьютере конфигурации, указанной выше.
Количество при замене элементов трех блоков водяного экономайзера суперэлементами составило 322500 – 188460 = 134040 плюс 3 суперэлемента с рассчитанными матрицами жесткости, масс и демпфирования, при этом время расчёта водяного экономайзера составило менее 50 минут, т.е. сократилось в 3 раза. Погрешность при сравнении перемещений контрольных точек составила меньше 1 %. Динамический расчёт на сейсмическое воздействие был выполнен лишь после замены блоков конвективных пароперегревателей низкого давления на элементы с сосредоточенной массой.
Выводы
1. Комплексное применение рассмотренных методик позволяет получать эффективные модели сложных конструкций при высокой точности расчёта, снижении трудозатрат на формирование моделей и длительности вычислительных операций, практически снимает ограничения по мощности используемых компьютеров.
2. Совместное и последовательное использование методик построения оптимальных геометрических моделей и субмоделирования повышает точность расчёта, более чем в 10 раз снижает трудоёмкость формирования моделей и на порядки уменьшает длительность вычислений.
3. Использование суперэлементов при моделировании котельных конструкций в несколько раз уменьшает длительность вычислительных операций и существенно расширяет круг задач, моделирование которых может быть проведено на компьютерах со средними по мощности характеристиками.
Библиографическая ссылка
Курепин М.П., Сербиновский М.Ю. ЭФФЕКТИВНЫЕ МЕТОДИКИ КОНЕЧНО-ЭЛЕМЕНТНОГО МОДЕЛИРОВАНИЯ СЛОЖНЫХ КОНСТРУКЦИЙ ЭНЕРГЕТИЧЕСКОГО МАШИНОСТРОЕНИЯ // Современные наукоемкие технологии. 2017. № 10. С. 19-25;URL: https://top-technologies.ru/ru/article/view?id=36822 (дата обращения: 28.01.2026).



