Особенностью методологии исследований в педагогике, определяющей логическую организацию, структуру, методы и средства деятельности, является важная роль субъективного фактора. Так, при определении полноты знаний обучающегося (объекта исследований) в качестве эталона измерений выступает полнота знаний преподавателя (субъекта). На результат измерения полноты знаний обучающегося безусловно оказывает влияние психосоматическое состояние как обучающегося, так и преподавателя, которое несет в себе элементы случайности. Необходимо также принимать во внимание, что результат измерения также зависит от предыстории, а именно от случайного характера поведения обучающегося в процессе усвоения знаний.
Для уменьшения влияния субъективного фактора в процессе измерений используются технические средства, например компьютер, который ставится между субъектом и объектом измерений с целью проведения компьютерного тестирования полноты знаний. Однако формулирование вопросов тестирования, ранжирование их по степени важности и присвоение им весовых коэффициентов, оценка полноты охвата ими изучаемого материала и т.п. осуществляются преподавателем, поэтому полностью устранить влияние субъективного фактора на процесс педагогического измерения технические средства не могут.
При проведении педагогических измерений важную роль играет операция упорядочения эмпирических данных путем перевода их в шкальные оценки, т.е. шкалирование. В отличие от точных наук, в которых измерение сводится к сравнению данной величины с однородной ей величиной, принятой за единицу (с объективно существующим эталоном), при измерении педагогических параметров эталон сравнения всегда субъективен. Более того, большинство психолого-педагогических параметров (признаки, свойства, качества и т.п.) являются латентными (скрытыми), судить о которых можно лишь косвенно, по их проявлениям, т.е. весьма приближенно. Так, полнота знаний обучающегося является функцией нескольких макропараметров, таких как уровень предшествующих знаний, способность к обучению, внимание, память, качество ассоциаций, трудолюбие, психосоматическое состояние, внешние условия и т.п. В свою очередь, каждый из них является результатом большого числа микропроцессов, происходящих на клеточном или даже молекулярном уровнях, и различных микропараметров. Шкалирование предполагает выбор подходящей шкалы, которая должна отвечать задачам измерения и учитывать особенности свойств объекта измерений. В связи с этим кратко рассмотрим модель обучающегося, описывающую его поведение в процессе усвоения знаний.
Модель обучающегося
Успешность любой деятельности человека, в том числе и его участия в процессе обучения, зависит от уровня развития сознания. В [3] показано, что детерминизм сознания индивида реализуется через случайность, обусловленную внутренне присущим случайным характером психического и соматического состояний индивида. Кроме того, в работе [6] отмечается, что реальный процесс мышления существенно возмущается физиологическим, психологическим и информационным шумами головного мозга. Физиологический шум производится одновременной работой огромного числа нейронов (физическими и биохимическими процессами в мозге). Психологический шум обусловлен флуктуациями психического состояния человека. Информационный шум производится как внешней информацией, так и одновременной работой огромного числа мыслящих систем, находящихся в мозге.
Шум в процессе мышления может играть как отрицательную (разрушительную) роль, так и важную положительную. Некоторые комбинации шумовых процессов могут производить идеи, которые не могли бы появиться как результат строго детерминистского процесса мышления. С другой стороны, некоторый специфический набор шумовых процессов, зависящий от конкретной мыслящей системы, даже при низкой интенсивности может полностью нарушить процесс мышления. Шум, разрушительный для одного мозга, может иметь положительный эффект для другого. В этом случае при описании процессов мышления вместо модели детерминистской динамической системы необходимо использовать модель случайной динамической системы [6].
Следовательно, знания обучающегося, являющиеся фактически продуктом сознания, также несут в себе элементы случайности. В связи с этим для описания поведения обучающегося в процессе усвоения знаний в [3] было предложено использовать неклассический вероятностно-статистический метод, в соответствии с которым обучающийся идентифицируется функцией распределения (плотностью вероятности), движущейся в информационном пространстве координат, скоростей и ускорений различных порядков. Это означает, что нельзя указать точное положение обучающегося в информационном пространстве, можно лишь говорить о вероятности нахождения его в той или иной области информационного пространства. Следует отметить особенность неклассического вероятностно-статистического метода исследований, отличающую его от классического тем, что он применяется не только к массовым, но и к отдельным событиям, имеющим внутренне присущий им случайный характер [5].
Функции распределения, которыми идентифицируются обучающиеся, являются решениями дифференциальных уравнений, полученных на основе закона сохранения вероятности. Они представляют собой уравнения непрерывности, связывающие изменение плотности вероятности за единицу времени в фазовом пространстве координат, скоростей и ускорений различных порядков с дивергенцией потока плотности вероятности. После несложных преобразований уравнения непрерывности, представленные в [3], могут быть записаны в следующем виде:
……….......................................……….,
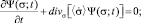
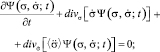
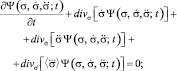
где Ψ(σ; t),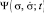 
и 
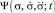– функции распределения, идентифицирующие обучающегося в информационном пространстве; σ, 
, 
, 
, 
, 
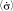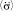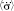– координата, скорость, средняя скорость, ускорение первого порядка, среднее ускорение первого порядка и среднее ускорение второго порядка индивида соответственно; t – время.
Данная система состоит из бесконечного числа уравнений, и вопрос о том, какое из приведенных уравнений использовать для нахождения функции распределения, зависит от возможности получения данных о средних значениях скорости и ускорений различных порядков. Так, если известно значение средней скорости, то можно по известным начальному и граничному условиям найти решение первого уравнения из приведенной выше системы дифференциальных уравнений. В этом случае решением должна быть функция аргумента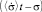 
, т.е. 
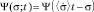, в чем легко убедиться, подставив данную функцию в первое уравнение из приведенной системы дифференциальных уравнений. Такими функциями распределения в зависимости от начальных и граничных условий могут быть, например, функции, соответствующие закону нормального распределения, а также распределениям в виде дельта-функции Дирака, в виде прямоугольной функции и др. Второе уравнение из данной системы также может быть решено аналитически. Функция распределения в этом случае представляет собой суперпозицию двумерных волн, распространяющихся в информационном пространстве координат и скоростей [3]. Решение уравнений более высокого порядка, вероятно, возможно только численным методом.
Данные уравнения непрерывности позволяют прогнозировать поведение индивидуальных функций распределения в пространстве и во времени, а следовательно, и поведение индивидов, выполняющих определенную деятельность, поскольку последние идентифицируются этими функциями. Это есть проявление неклассического детерминизма, реализующегося через случайность.
Как отмечалось выше, при проведении педагогических измерений большое внимание уделяется вопросам шкалирования. Поскольку поведение обучающегося имеет вероятностно-статистический характер, классические методы шкалирования для измерения полноты знаний не могут быть использованы. В связи с этим для решения данной проблемы был предложен вероятностно-статистический метод шкалирования [4].
Вероятностно-статистическое шкалирование
В соответствии с [4] шкала измерений при определении полноты знаний обучающегося представляет собой упорядоченную систему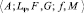 
. Здесь A – некоторое вполне упорядоченное множество объектов (обучающихся), обладающих интересующими нас признаками (эмпирическая система с отношениями); Lψ – функциональное пространство (пространство функций распределения) с отношениями; F – операция гомоморфного отображения A в подсистему Lψ (идентификация обучающихся функциями распределения); G – группа допустимых преобразований над функциями распределения; f – операция отображения функций распределения из подсистемы Lψ на числовые системы с отношениями n-мерного пространства M, которая представляет собой нахождение моментов различных порядков функций распределения.
Поскольку работать в функциональном пространстве чрезвычайно сложно, данная шкала измерений позволяет при оценке полноты знаний обучающихся, которые идентифицируются функциями распределения, перейти из функционального пространства в числовое пространство. Это осуществляется путем расчета моментов экспериментально найденных индивидуальных функций распределения. Методика расчета моментов функций распределения изложена в работе [4]. Рассмотрим основные свойства экспериментальных функций распределения обучающихся.
Экспериментальные функции распределения
При использовании классической пятибалльной шкалы измерений погрешность измерения полноты знаний обучающегося составляет ±0,5 балла. Это означает, что, когда обучающийся получает, например, оценку 3 балла, его знания находятся в промежутке от 2,5 до 3,5 баллов. Следовательно, в данном случае положение обучающегося в информационном пространстве определяется прямоугольной функцией распределения, ширина которой равна 1 баллу, а оценка является фактически математическим ожиданием (рис. 1). При таком измерении полноты знаний индивидуальные функции распределения обучающихся совпадают и, следовательно, в данном случае действует принцип неразличимости, т.е. отсутствует возможность в пределах данной оценки тонкого ранжирования студентов по уровню знаний. Погрешность измерения в этом случае настолько большая, что не позволяет выявлять структурные особенности индивидуальных функций распределения.
Значительно большие возможности в этом плане предоставляют балльные шкалы более высокого порядка, например двадцатибалльная шкала. На рис. 2 при использовании двадцатибалльной шкалы изображены типичные индивидуальные функции распределения студентов, представляющие собой фактически гистограммы, которые трудно аппроксимировать гладкими линиями.
Видно, что индивидуальные функции распределения обучающихся располагаются в разных областях информационного пространства и имеют различную структуру, т.е. в данном случае работает так называемый принцип «различимости». Это свидетельствует о том, что моменты представленных функций распределения имеют различные значения (таблица).
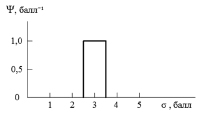
Рис. 1. Типичный вид функции распределения, идентифицирующей студента, получившего на экзамене оценку «удовлетворительно» (3 балла) по пятибалльной шкале
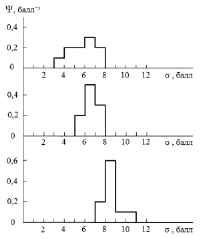
Рис. 2. Типичный вид функций распределения, идентифицирующих студентов, получивших на экзамене традиционную оценку «удовлетворительно» (3 балла) по двадцатибалльной шкале
Моменты функций распределения студентов, получивших на экзамене по физике традиционную оценку «3»
|
№ п/п |
Порядок момента |
||||||
|
μ1, балл |
μ2, балл2 |
μ3, балл3 |
μ4, балл4 |
μ5, балл5 |
μ6, балл6 |
μ7, балл7 |
|
|
1 |
5,80 |
1,61 |
–0,58 |
5,11 |
–4,29 |
20,63 |
–27,07 |
|
2 |
6,60 |
0,49 |
–0,05 |
0,50 |
–0,15 |
0,51 |
–0,25 |
|
3 |
8,60 |
0,69 |
0,49 |
1,66 |
2,21 |
5,11 |
8,60 |
В большинстве случаев, как показывает опыт, достаточно ограничиться расчетом моментов первого порядка μ1 (математического ожидания), второго порядка μ2 (дисперсии) и третьего порядка μ3, характеризующего асимметрию функции распределения. Сравнение значений найденных моментов индивидуальных функций распределения позволяет осуществлять тонкое ранжирование обучающихся по уровню знаний. При стремлении порядка балльности измерительной шкалы к бесконечности функции распределения обучающихся будут стремиться к истинным функциям распределения. Аналогичную структуру индивидуальные функции распределения имеют и для студентов, получивших на экзамене оценки «отлично» (5 баллов), «хорошо» (4 балла) и «неудовлетворительно» (2 балла).
В приближении аддитивности индивидуальных функций распределения легко провести их статистическую обработку. С этой целью воспользуемся результатами измерений полноты знаний студентов по физике с помощью классического и вероятностно-статистического шкалирований [3]. Так, для потока студентов, состоящего из 56 обучающихся, 7 студентов получили традиционную оценку «5» баллов, 17 студентов – «4» балла, 28 студентов – «3» балла и 4 студента – «2» балла. Используя результаты измерений полноты знаний данной группы студентов, полученные с помощью вероятностно-статистического шкалирования, авторы построили индивидуальные функции распределения для каждого студента и провели их статистическую обработку. На рис. 3 изображены усредненные индивидуальные функции распределения обучающихся, соответствующие указанным выше группам студентов.
Анализ этих функций распределения показывает, что не существует четко очерченных границ между полнотой знаний студентов, получивших на экзамене традиционные оценки «5» и «4», «4» и «3», «3» и «2». Функции распределения приграничных областей перекрываются. Как отмечалось выше, в процессе измерения полноты знаний обучающегося последний взаимодействует с преподавателем, действия которого также несут в себе элементы случайности, что, естественно, сказывается на результате измерения. Однако получить в явном виде влияние преподавателя на процесс измерения полноты знаний обучающегося не удается, т.к. оно носит латентный характер.
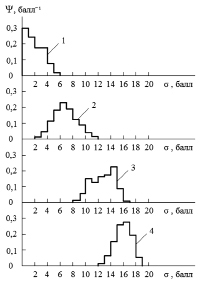
Рис. 3. Типичный вид усредненных функций распределения, идентифицирующих студентов, получивших на экзамене по двадцатибалльной шкале традиционные оценки: 1 – «неудовлетворительно» (2 балла); 2 – «удовлетворительно» (3 балла); 3 – «хорошо» (4 балла); 4 – «отлично» (5 баллов)
Полнота знаний студента непосредственно зависит от его взаимодействия с профессорско-преподавательским коллективом в процессе обучения. В [3] проведен анализ такого взаимодействия и установлено, что в линейном приближении скорость движения математического ожидания индивидуальных функций распределения студентов в информационном пространстве пропорциональна функции воздействия профессорско-преподавательского коллектива и обратно пропорциональна функции инертности, характеризующей неподатливость изменению положения математического ожидания в пространстве, а именно
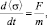
где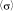 
– математическое ожидание индивидуальной функции распределения обучающегося; F – функция воздействия на обучающегося со стороны профессорско-преподавательского коллектива, зависящая от профессиональных и личностных характеристик каждого; m – функция, характеризующая инертность (неподатливость) обучающегося по отношению к изменению его положения в информационном пространстве и зависящая от личностных характеристик индивида.
Данное уравнение является фактически аналогом уравнения движения Аристотеля в механике, роль силы в котором выполняет функция воздействия, а массы – функция инертности. Следует отметить, что уравнение движения математического ожидания индивидуальной функции распределения является классически детерминированным и, следовательно, позволяет рассчитать для известных функций F и m положение математического ожидания в информационном пространстве в любой момент времени. Однако получение информации о свойствах этих функций представляет собой чрезвычайно сложную задачу и требует проведения глубоких психолого-педагогических исследований профессорско-преподавательской и студенческой подсистем.
Сейчас достигнуты большие успехи в разработке теоретических и практических основ измерений в педагогике, однако в целом проблема измерений еще далека от решения. Это, прежде всего, связано с тем, что в настоящее время еще нет достаточной информации о влиянии сознания человека на процесс измерения. Подобная ситуация сложилась и в квантовой механике. Так, рассматривая проблемы квантовых измерений, автор работы [2] пришел к выводу, что объяснить ряд парадоксов измерений в квантовой механике «…вряд ли возможно без непосредственного включения сознания наблюдателя в теоретическое описание квантового измерения». Далее утверждается, что «…непротиворечивым является предположение о том, что сознание может сделать вероятным некоторое событие, даже если по законам физики (квантовой механики) вероятность этого события мала. Сделаем важное уточнение формулировки: сознание данного наблюдателя может сделать вероятным, что он увидит это событие».
Данные утверждения основаны на интерпретации квантовой механики, предложенной в работе [7], в соответствии с которой объект измерения, измерительный прибор и наблюдатель образуют единую квантовую систему. В этой системе подсистемы «объект и измерительный прибор» и «наблюдатель» взаимодействуют друг с другом. Кстати, измерительный прибор в такой системе может и отсутствовать, а его роль будет выполнять непосредственно наблюдатель. Поведение такой системы можно описать с помощью уравнения Шредингера и получить решения, соответствующие возможным классическим альтернативам (состояниям) объекта измерения. Сознание наблюдателя в [2] отождествляет с выбором той или иной альтернативы объекта измерения («…мы предполагаем, что селекция альтернативы должна быть отождествлена с сознанием»). В данной работе говорится также о том, что сознание является общей частью квантовой физики и психологии и, следовательно, предоставляет новые возможности в познании действительности. Тот факт, что сознание наблюдателя, как утверждается в [2], может сделать вероятной (реализуемой на практике) любую из классических альтернатив измеряемой квантовой системы, говорит о случайном характере сознания. Это является еще одним подтверждением, что детерминизм сознания человека реализуется через случайность.
Следует отметить схожесть поведения человека при выполнении им той или иной деятельности с поведением квантовых микрочастиц (электронов, атомов и др.). Так, поведение человека и микрочастиц в соответствии с копенгагенской интерпретацией квантовой механики имеет вероятностно-статистический характер. Уравнение Шредингера, описывающее поведение микрочастиц, можно преобразовать к уравнению непрерывности, совпадающему по форме записи с первым уравнением из приведенной выше системы дифференциальных уравнений [1]. Однако имеются и существенные различия, основные из которых следующие. Во-первых, в квантовой механике действует принцип «неразличимости», в соответствии с которым все микрочастицы одинаковые и их невозможно отличить друг от друга, в то время как при описании поведения человека учитываются индивидуальные особенности каждого, т.е. действует принцип «различимости». Во-вторых, уравнение Шредингера описывает случайный характер поведения микрочастиц только в координатном пространстве, а случайный характер поведения индивида представляется возможным описать не только в координатном пространстве, но и в пространствах скоростей и ускорений различных порядков.
Выводы
1. В процессе измерения полноты знаний обучающегося фактор случайности играет принципиальную роль, поскольку детерминизм поведения как обучающегося, так и преподавателя реализуется через случайность. В связи с этим для описания поведения обучающегося был использован неклассический вероятностно-статистический метод. В соответствии с этим методом обучающийся идентифицируется функцией распределения, которая находится в результате измерения полноты знаний и характеризует ее. На результат измерения, естественно, влияет и случайный характер поведения преподавателя, однако это влияние носит латентный характер и не проявляется в явном виде.
2. Сравнительный анализ результатов измерений полноты знаний обучающихся, полученных при использовании классического балльного шкалирования и вероятностно-статистического шкалирования, показал, что последнее дает гораздо больше информации о полноте знаний и позволяет тонко ранжировать обучающихся по уровню знаний.
3. Уравнения непрерывности, решением которых являются функции распределения, отражают единство случайности и детерминизма. В данном конкретном случае детерминизм поведения обучающегося в процессе усвоения знаний реализуется через случайность.
4. Дальнейшие успехи на пути решения проблемы измерений в педагогике и науке в целом будут во многом зависеть от достижений в понимании сути сознания человека и его влияния на процесс измерений.
Библиографическая ссылка
Романов В.П., Ширяева Н.А. РОЛЬ ФАКТОРА СЛУЧАЙНОСТИ ПРИ ИЗМЕРЕНИИ ПОЛНОТЫ ЗНАНИЙ ОБУЧАЮЩЕГОСЯ // Современные наукоемкие технологии. – 2017. – № 6. – С. 157-163;URL: https://top-technologies.ru/ru/article/view?id=36717 (дата обращения: 03.12.2024).