Стержни широко применяются в различных машиностроительных сооружениях и приборах. При этом условия работы и взаимодействия стержней с другими элементами конструкции исключительно многообразны [5]. Так, например, трансмиссионные валы испытывают различные виды нагрузок. В силу неуравновешенности масс, работы муфт с перекосом трансмиссионные валы помимо основных крутильных нагрузок испытывают продольные и поперечные нагрузки. Для предотвращения опасных вибраций, снижения динамических нагрузок совершенствуются компенсирующие свойства упругих муфт [8], разрабатываются новые материалы конструкций. Поэтому развитие методов расчета динамических характеристик неоднородных стержневых систем, а также разработка программного обеспечения, реализующего уточненные методики, продолжают оставаться актуальными.
Авторская программа [2] MOCODISS (Моделирование континуально-дискретных систем) позволяет проектировать и производить расчеты на прочность континуально-дискретных систем, представленных неоднородным стержнем и подсистемой дискретных масс на вязкоупругом основании. Пакет состоит из модулей подготовки данных, расчета и анализа результатов. Модуль расчета основан на методе сплайн-преобразования координат.
Теоретические основы сплайн-аппроксимаций заложены в трудах Дж. Алберга [1], Э. Нильсона, Дж. Уолша, А. Сарда, С. Вейнтрауба и др. Значительный вклад внесли В.А. Лазарян, С.И. Конашенко [7], Е.Т. Григорьев, Н.Б. Тульчинская, А.К. Юсупов [9] и др.
В работе изложен принцип построения основных расчетных схем программного пакета MOCODISS. Обсуждаются основные идеи математического аппарата. Рассмотрен пример расчета известной в литературе задачи о колебаниях крыла самолета [4]. Приведен расчет низших частот поперечных колебаний, перемещений и усилий трансмиссионного вала автомобилей УАЗ при вариациях длины шлицевого соединения.
Основная расчетная схема MOCODISS
В расчетной схеме MOCODISS неоднородный по жесткости и массе стержень аппроксимируется большим числом однородных, за исключением точечных включений в массу, стержней, связанных вязкоупругими шарнирами с двумя степенями свободы сравнительно малой жесткости 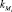 и
и 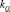 . Коэффициент
. Коэффициент 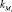 соответствует угловой жесткости шарнира,
соответствует угловой жесткости шарнира, 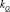 – поперечной. Каждый однородный стержень такой системы имеет неоднородное вязкоупругое основание, точечную массу Mrq в сечении x = drq, вязкоупругое защемление и опору жесткости k2rq и k1rq (
– поперечной. Каждый однородный стержень такой системы имеет неоднородное вязкоупругое основание, точечную массу Mrq в сечении x = drq, вязкоупругое защемление и опору жесткости k2rq и k1rq (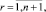
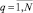 ) соответственно.
) соответственно.
Основная расчетная схема MOCODISS позволяет проводить исследование поперечных колебаний неоднородного стержня с подсистемой дискретных масс, связанных между собой, неподвижным основанием и с некоторыми сечениями x = drq стержня вязкоупругими связями.
Такая расчетная схема может быть использована при анализе различных строительных конструкций, узлов машин и установок, например колонных аппаратов химических производств и других объектов. В частности, при моделировании коренных валов, несущих основные рабочие органы машины, а также валов передач. Упругие шарниры расчетной схемы позволяют исследовать движение валов, соединенных цилиндрическими шарнирами [6], упругими муфтами. Возможен учет промежуточных опор и закрепленных масс.
Таким образом, приведенная расчетная схема охватывает довольно большой класс элементов машиностроительных конструкций, объединенных общим математическим описанием.
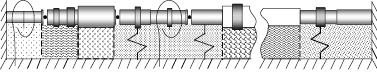
Рис. 1. Пример неоднородного стержня основной расчетной схемы MOCODISS
Краткое описание математической модели
Математическая модель вибрационных поперечных колебаний такой стержневой системы [2] приводит к начально-краевой задаче (1)–(3):
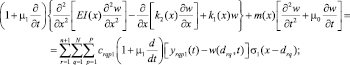
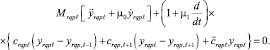 (1)
(1)
w(x, 0) = w0(x); 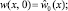
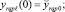
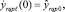 (2)
(2)
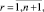
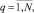
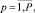
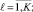
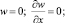
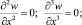
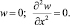 (3)
(3)
Здесь w(x, t), yrqpl (t) – перемещения стержня и масс Mrqpl ; crqpl – жесткость упругой связи дискретных масс p-й цепочки, закрепленной в сечении x = drq; 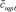 – жесткость упругой связи массы Mr qp с неподвижным основанием; σ0 и σ1 – функции единичного скачка и Дирака; μ0 и μ1 – внешние и внутренние диссипативные коэффициенты; EI(x) и m(x) – параметры жесткости и массы неоднородного стержня, удовлетворяющие условиям (4) и (5) соответственно; k1(x) и k2(x) – характеристики неоднородного основания (6).
– жесткость упругой связи массы Mr qp с неподвижным основанием; σ0 и σ1 – функции единичного скачка и Дирака; μ0 и μ1 – внешние и внутренние диссипативные коэффициенты; EI(x) и m(x) – параметры жесткости и массы неоднородного стержня, удовлетворяющие условиям (4) и (5) соответственно; k1(x) и k2(x) – характеристики неоднородного основания (6).
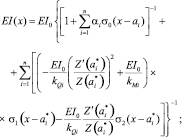 (4)
(4)
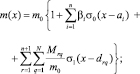 (5)
(5)
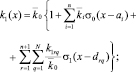
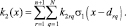 (6)
(6)
В (4)–(6) и далее 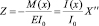 – приведенный изгибающий момент M(x); EI0, m0 и
– приведенный изгибающий момент M(x); EI0, m0 и 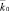 – параметры жесткости и массы стержня, и упругого основания при 0 < x < a1; I(x) момент инерции сечения стержня в точке x; I(x) = I0 при 0 < x < a1; αi, βi и
– параметры жесткости и массы стержня, и упругого основания при 0 < x < a1; I(x) момент инерции сечения стержня в точке x; I(x) = I0 при 0 < x < a1; αi, βi и 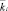 – коэффициенты скачков параметров стержня и основания в сечениях x = ai. Для преобразований формул принято, что точечные включения в жесткость стержня расположены в сечениях
– коэффициенты скачков параметров стержня и основания в сечениях x = ai. Для преобразований формул принято, что точечные включения в жесткость стержня расположены в сечениях 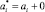 .
.
Применяя классический метод решения начально-краевой задачи (1)–(3), находятся частные нетривиальные решения T(t)X(x) и Arqpl T(t) подсистемы (1), удовлетворяющие краевым условиям (3). Для определения амплитуд Arqpl дискретных масс rqp-й цепочки найдены рекуррентные формулы относительно перемещений сечений x = drq стержня.
Далее, задача о совместных колебаниях неоднородного стержня и подсистемы масс сводится [3] к формулировке (7), соответствующей проблеме колебаний неоднородного стержня с жестко присоединенными приведенными массами (8).
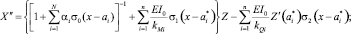
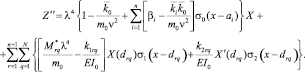 (7)
(7)
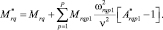 (8)
(8)
Выражение 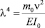 в (7) задает собственные значения системы.
в (7) задает собственные значения системы.
Затем, применив к уравнениям (7) сплайн-преобразование
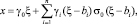
получаем уравнение (9) с постоянными коэффициентами в правой и сингулярностями высокого порядка в левой части уравнения
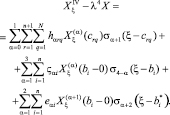 (9)
(9)
В (9) коэффициенты hαrq , ζαi, eαi зависят от параметров стержневой системы [3].
Применяя операционный метод к уравнению (9), исключив коэффициенты 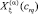 и
и 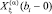 , получено [3] аналитическое выражение для собственных форм в виде
, получено [3] аналитическое выражение для собственных форм в виде
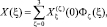 (10)
(10)
где Φζ(ξ), 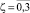 – принято [7] интерпретировать как обобщенные функции А.Н. Крылова.
– принято [7] интерпретировать как обобщенные функции А.Н. Крылова.
Найденные аналитические выражения обобщенных функций А.Н. Крылова позволили из (3) определить собственные значения λs (s = 1, 2, 3...) континуально-дискретной системы. Далее, используя обратное сплайн-преобразование
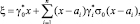
найдены собственные формы в начальной системе координат.
Представленный математический аппарат составляет основу расчетного модуля программного пакета MOCODISS.
Сравнительный анализ
Для подтверждения точности разработанных алгоритмов проводились [2], [3] многочисленные сравнения с известными в литературе точными и численными решениями, а также решениями сторонних программных пакетов, реализующих метод конечных элементов. В качестве примера рассмотрим известную задачу о собственных колебаниях консольного стержня [4], высота которого уменьшается по линейному закону, а ширина равна единице (рис. 2).
Стержень разбивается на десять равных частей длиной 0,1•L. Жесткость стержня на первом участке равна 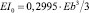 , интенсивность массы – m0 = 0,4667•bρ, где ρ = 7,8•103 кг/м3 – плотность материала, E = 2•1011 Па – модуль упругости. Величина скачков жесткости αi (4) соответственно равна 1,29; 2,11; 3,14; 4,37; 5,80; 7,44; 9,30; 11,34; 13,66, а интенсивности массы βi = 0,333,
, интенсивность массы – m0 = 0,4667•bρ, где ρ = 7,8•103 кг/м3 – плотность материала, E = 2•1011 Па – модуль упругости. Величина скачков жесткости αi (4) соответственно равна 1,29; 2,11; 3,14; 4,37; 5,80; 7,44; 9,30; 11,34; 13,66, а интенсивности массы βi = 0,333, 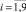 . Длина стержня L = 15 м, высота b = 0,25 м.
. Длина стержня L = 15 м, высота b = 0,25 м.
В табл. 1 приведены результаты расчетов для трех низших собственных частот νi, соответствующих им значений 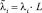 и точные значения коэффициентов
и точные значения коэффициентов 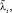
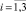 . В работе [4] приводятся точные значения коэффициентов φi частоты νi: φ1 = 2,48; φ2 = 9,12; φ3 = 21,3. Величины φi и
. В работе [4] приводятся точные значения коэффициентов φi частоты νi: φ1 = 2,48; φ2 = 9,12; φ3 = 21,3. Величины φi и 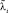 в данном случае связаны соотношением
в данном случае связаны соотношением 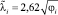 [7]. Как видно из табл. 1, точные значения
[7]. Как видно из табл. 1, точные значения 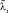 и вычисленные по программе MOCODISS достаточно близки.
и вычисленные по программе MOCODISS достаточно близки.
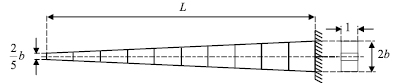
Рис. 2. Консольный стержень
Таблица 1
Собственные частоты νi (Гц) и соответствующие им числа 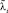 консольного стержня
консольного стержня
|
i |
MOCODISS |
Точное значение |
|
|
νi |
|
|
|
|
1 |
44,47506 |
4,134 |
4,134 |
|
2 |
162,83863 |
7,910 |
7,909 |
|
3 |
381,42888 |
12,107 |
12,105 |
Вычислительные эксперименты
В следующих вычислительных экспериментах исследована зависимость низших частот колебаний трансмиссионного вала автомобиля от длины шлицевого соединения. Общая расчетная схема карданной передачи автомобиля может быть представлена на рис. 3.
Для определенности на рис. 3 приведены геометрические размеры переднего трансмиссионного вала автомобилей УАЗ-3741, УАЗ-3962, УАЗ-2206, УАЗ-3303. Шлицевое соединение вала изменяется в диапазоне от 0 до 54 мм. В расчетах предполагается, что каждая часть ступенчатого стержня однородна и выполнена из стали (E = 2•1011 Па, ρ = 7,8•103 кг/м3). Параметры стержневой системы приведены в табл. 2.
Результаты исследования зависимости собственных частот карданного вала от изменения в указанном диапазоне значений Δx приведены на рис. 4.
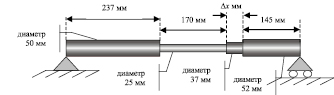
Рис. 3. Общая расчетная схема карданной передачи автомобиля
Таблица 2
Таблица параметров стержневой системы
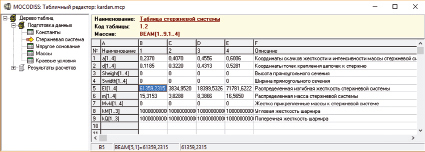
Рис. 4. Зависимость пяти низших частот карданного вала от изменения Δx в диапазоне от 0 до 54 мм
 а
а 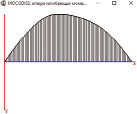 б
б 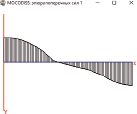 в
в
 г
г
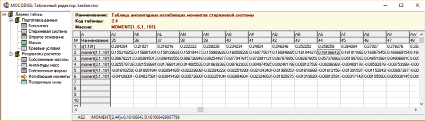
Рис. 5. Модальные окна MOCODISS в режиме результатов расчета: а – первая форма колебаний (L = 0,6006 м, частота 796,21 Гц); б – эпюра изгибающих моментов; в – эпюра поперечных сил; г – таблица изгибающих моментов
Как видно из рис. 4, удлинение карданного вала за счет подвижного шлицевого соединения приводит к уменьшению значений собственных частот. При этом значительно уменьшаются только высшие частоты. Диапазон изменения основной частоты поперечных колебаний вала при допустимых вариациях шлицевого зазора составил от 784,2 до 920,5 Гц.
С увеличением длины вала увеличиваются и максимальные смещения сечений. Результаты расчетов форм собственных колебаний и амплитудных усилий карданного вала, соответствующих длине – 0,6006 м, изображены на рис. 5.
Максимальные смещения первой формы колебаний достигаются на участке второй ступени с наименьшим диаметром поперечного сечения при x = 312 мм. Максимальное значение приведенного изгибающего момента равно 0,161 Н•м2 при x = 258 мм.
Заключение
Сравнение результатов расчета с известным точным решением доказывает высокую эффективность алгоритмов MOCODISS. Вычислительные эксперименты показали применимость основных расчетных схем программного пакета MOCODISS для задач динамики трансмиссионных валов с подвижным шлицевым соединением. Выявлен диапазон изменения низших частот, максимальных смещений и усилий при изменении длины шлицевого соединения трансмиссионного вала автомобилей УАЗ.
Разработанный программный пакет MOCODISS найдет свое применение в расчете аппаратов колонного типа, опор электропередач, участков трубопровода и др.
Библиографическая ссылка
Архипов С.В. РАСЧЕТ ПОПЕРЕЧНЫХ КОЛЕБАНИЙ ТРАНСМИССИОННОГО ВАЛА В ПРОГРАММНОМ ПАКЕТЕ MOCODISS // Современные наукоемкие технологии. 2017. № 6. С. 12-17;URL: https://top-technologies.ru/ru/article/view?id=36690 (дата обращения: 15.02.2026).





