Болезни миокарда занимают центральное место в патологии сердца, поскольку практически любая недостаточность деятельности сердечно-сосудистых систем связана именно с мышечной недостаточностью миокарда, причем не только в случаях его самостоятельного заболевания. Исследования, выполненные ранее, показали [7, 12–14], что изменение формы миокардиальных волокон, их эпи- и эндокардиальная ротация, нарушение работы ионных каналов в местах с недостаточной перфузией закономерно приводят к изменениям в регистрируемом магнитном поле сердца. Однако магнитокардиография (МКГ) достаточно специфична и, несмотря на высокую чувствительность по отношению к изменениям миокарда, в том числе и в случаях, когда анализ ЭКГ неинформативен, а проведение нагрузочных проб противопоказано, имеет существенные недостатки, связанные в первую очередь с тем, что анализ результатов МКГ выполняется, в основном, на основании визуальной классификации карт, путем сравнения их с неким «образом» нормальной карты. Т.е. анализ результатов МКГ основывается на наиболее информативных, но плохо формализуемых признаках и правилах. Также визуальный анализ магнитокардиографических карт имеет существенные недостатки, свойственные визуальной классификации любых медицинских изображений, а именно: необходимость довольно длительного периода обучения и относительно слабая воспроизводимость результатов.
Основываясь на современных представлениях о том, что миокард сердца имеет топологию Мебиуса [5, 6, 10], было высказано теоретическое предположение [1], что для каждого момента времени кардиоцикла результат регистрации магнитных полей отражает функциональный статус миокарда, с точки зрения соответствия топологии исследуемого миокарда и топологии Мебиуса. Исследования, выполненные нами ранее [2], подтвердили гипотезу о влиянии топологии Мебиуса на распространение магнитного поля в магнитопроводе, что позволяет сделать вывод о высокой информативности регистрации напряженности магнитного поля и возможности его использования в целях диагностики и прогнозирования развития патологий в сердечно-сосудистой системе. Это делает актуальным исследование возможности характеристики функционального статуса миокарда по результатам измерения напряженности магнитного поля.
Научная новизна
Известно, что меридиан сердца [5] представляет собой тор с поверхностью Мебиуса. Учитывая, что характерные значения магнитных полей сердца составляют порядка 50 пкТл [4], предложенная нами математическая модель строилась в приближении гипотезы о влиянии топологии магнитопровода на его приведенные характеристики, в области малых интенсивностей магнитных полей, сопоставимых с влиянием собственной намагниченности структуры. Таким образом, в работе миокард сердца рассмотрен как совокупность магнитных доменов, которые связывают микроскопические магнитные характеристики с макроскопическими свойствами. Это делает актуальным с целью решения задачи оценки функционального резерва деятельности сердца охарактеризовать функциональный статус миокарда по результатам измерения напряженности магнитного поля, выполнить анализ влияния топологии магнитопровода на распространение магнитного поля вне магнитопровода.
Материалы и методы исследования
По аналогии с известной дипольной моделью сердца [5], на основании взаимосвязи электрического и магнитного полей принимаем, что магнитостатическое взаимодействие отдельных компонентов внутри объема намагниченного тела приводит к возникновению собственной магнитостатической энергии этого тела, величина которого может быть определена как
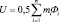, (1)
где Фi – магнитный потенциал, создаваемый всеми фиктивными магнитными зарядами ± mi, кроме i-го в месте расположения i-го заряда. Если принять, что магнитные заряды распределены в пространстве с плотностью ρ тогда выражение (1) удобно записать как
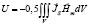, (2)
где V – объем магнетика, JS – намагниченность, Hm – напряженность.
Видно, что для пространства, заполненного магнитным материалом с намагниченностью JS, магнитостатическое взаимодействие отдельных элементов объема внутри намагниченного тела приводит к наличию собственной магнитостатической энергии этого тела, и величина поля рассеяния Hm ведет к образованию областей самопроизвольного намагничивания, т.е. доменной структуры. Это позволяет принять миокард сердца как магнитную доменную структуру – совокупность областей в магнитной подсистеме магнитных материалов, которые связывают микроскопические магнитные характеристики с их макроскопическими свойствами. Таким образом, при моделировании магнитного поля будем считать, что процессы намагничивания и перемагничивания определяются свойствами доменной структуры. Оценим влияние доменной структуры на распространение магнитного поля. Для оценки влияния неориентированной поверхности на распространение в ее объеме магнитного поля принимаем энергию анизотропии и обменных взаимодействий пренебрежимо малыми. Также пренебрегаем шириной доменных границ. С учетом сделанных упрощений, в расчетной модели принимаем, что магнитопровод (рис. 1, поз. 1) выполнен из ферромагнитного материала в виде тора с поверхностью Мебиуса и локальным расположением катушки намагничивания (рис. 1, поз. 2).
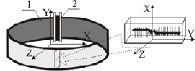
Рис. 1. Модель магнитопровода
а) б)
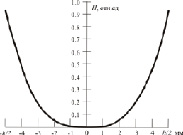
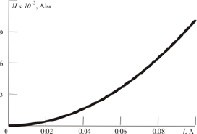
Рис. 2. Распространение электромагнитной волны: а – по сечению магнитопровода; б – в зависимости от силы тока I
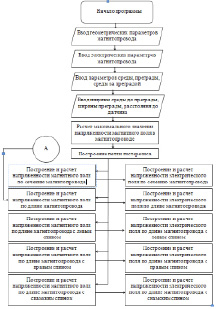
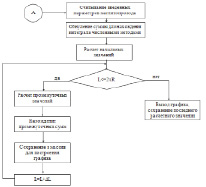
Рис. 3. Блок-схема
Известно, что ферримагнитные тела состоят из областей самопроизвольного намагничивания, векторы намагниченности которых направлены в различные стороны, причем система в целом будет обладать минимумом энергии, если области будут намагничены антипараллельно. Однако, если при решении задачи визуализации внутренней структуры миокарда сердца ферромагнитное тело поместить во внешнее магнитное поле, то под действием этого поля векторы намагниченности становятся параллельны [3]. Поэтому в модели принимаем, что векторы намагниченности направлены в одну сторону и «механически» меняют свое направление при прохождении «зоны Мебиусной закрутки».
С учетом сделанных допущений и упрощений выполним анализ распространения магнитного поля в торроидальном магнитопроводе с топологией Мебиуса и традиционном торроидальном исполнении. В расчетах принимали, что магнитопровод выполнен из ферромагнитного материала типа Magnifer с габаритными размерами: внутренний радиус – 40 мм, внешний радиус – 50 мм, сечение прямоугольное 10 мм. Ток частотой 50 Гц и силой до 1 А, вызывающий МДС, протекает через катушку с числом витков 100 (см. рис. 1).
Принимаем, что напряженность магнитного поля задается параметрами тока, текущего через катушку (см. рис. 1):
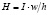, (3)
где h – ширина магнитопровода; I – сила тока, текущего через катушку; w – число витков.
Тогда распределение магнитного поля по сечению удобно определить относительно средней линии магнитопровода:
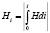, (4)
где i – шаг по сечению магнитопровода – h/2, (– h/2 + i), ...0, ... h/2 .
Распределение магнитной индукции по сечению соответственно:
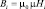, (5)
где В – магнитная индукция, μ0 = 4π•10–7 – магнитная постоянная составляющая, µ – магнитная проницаемость:
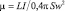, (6)
где S – площадь сечения магнитопровода; L – индуктивность.
Результаты расчета, демонстрирующие распространение магнитного поля по сечению магнитопровода и зависимость максимального значения напряженности от силы тока приведены на рис. 2. Видно, что напряженность поля по средней линии магнитопровода намного меньше напряженности поля на его поверхности (рис. 2, а). Неравномерный характер распределения электромагнитной волны качественно соответствует известным представлениям [11] и связан с возникновением магнитного поверхностного эффекта, вызванного затуханием электромагнитной волны. Также видно, что с ростом силы тока, текущего через катушку (рис. 2, б), напряженность магнитного поля нелинейно возрастает и на принятом расчетном интервале силы тока до 0,1 А находится на начальном нелинейном участке, что делает значимым влияние потерь в магнитопроводе.
а)
б)
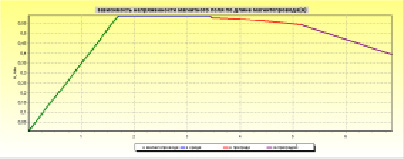
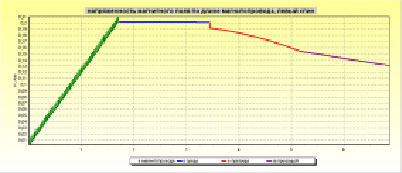
Рис. 4. График изменения напряженности магнитного поля: а – базовая топология магнитопровода; б – топология Мебиуса
Пренебрегая потерями на вихревые токи, будем считать, что при периодическом намагничивании ферромагнитного материала потери в сердечнике обусловлены потерями на гистерезис. Оценим влияние гистерезиса методом Релея [11]. Для оценки уровня потерь на гистерезис определим намагничиваемость:
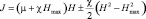, (7)
где c – магнитная восприимчивость, Hmax – наибольшее значение напряженности, достигаемое в материале сердечника (см. рис. 2, б).
Тогда магнитная индукция определяется
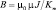, (8)
где Km – коэффициент намагничиваемости материала сердечника.
Будем считать, что физические потери на гистерезис обусловлены доменной структурой магнитопровода (см. рис. 1). Также следует отметить, что значительно большая напряженность поля на периферии магнитопровода, по сравнению с его средней плоскостью, показывает необходимость оценить, как влияет при закручивании магнитопровода в петлю Мебиуса то, что внутренний диаметр переходит во внешний и наоборот. Описание поверхности тора в традиционном исполнении и с поверхностью Мебиуса выполним по аналогии с описанием геометрии зацепления кольцевых винтовых передач 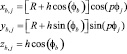[9]:
, (9)
где x, y, z – проекция на координаты (см. рис. 1); b, j – индексы дискретизации по осям х, y соответственно; R, r – внешний и внутренний радиус соответственно; φb, φj – углы закручивания в направлении осей х, y соответственно; p – шаг.
.
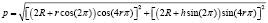При скручивании тора в поверхность Мебиуса деформация доменов происходит в плоскости xy. Тогда, полагая, что домены ориентированы в плоскости xy в направлении периферии, можно записать:
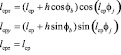, (10)
где lср – длина средней линии магнитопровода; lсрx, lсрy, lсрz – проекция средней линии магнитопровода на оси х, y, z соответственно.
Алгоритм расчета (1–10) приведен на рис. 3.
Результаты исследования и их обсуждение
Видно (рис. 4), что изменение топологии, при прочих равных начальных условиях, приводит к изменению напряженности магнитного поля на периферии магнитопровода и как следствие величины напряженности магнитного поля на удалении, в том числе за преградой, в качестве которой, в приведенных графиках рассмотрен такой неферромагнитный материал, как кожа. Видно, что максимальное значение напряженности магнитного поля для торроидального магнитопровода базовой топологии и мебиусной топологии различается в 2,9 раза, с 0,59 А/м до 0,20 А/м. Это приводит к изменению напряженности магнитного поля на удалении от магнитопровода, на расстоянии за преградой – также в 3 раза, с 0,39 А/м до 0,13 А/м.
Большинство высокочувствительных магнитометров измеряют индукцию магнитного поля, характер изменения индукции по мере удаления от магнитопровода аналогичен рис. 4, и величина индукции на расстоянии за преградой также изменяется в 3 раза, с 4,95 Тл до 1,65 А/м. Применительно к миокарду сердца это позволяет предположить о возможности функциональной диагностики путем измерения интенсивности магнитного поля, которое различается для нормального (скрученного миокарда) и патологий.
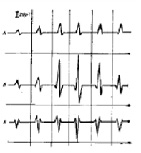
Рис. 5. Усредненные показатели QRS комплекса МКГ здоровых людей (А) с гипертрофией левого желудочка (Б) и с инфарктом миокарда (В) [8]
Вывод о влиянии патологии миокарда на напряженность магнитного поля коррелирует с известными результатами [8], также показывающими, что амплитуда сигнала регистрируемого магнитного поля здорового и больного человека различается (рис. 5), что качественно подтверждает достоверность предложенной модели.
Заключение
Работа направлена на решение проблемы совершенствования существующих методов МКГ-диагностики, основанных на регистрации наиболее информативного параметра электромагнитного поля сердца, описывающего функциональный статус миокарда.
Работа выполнена в приближении гипотезы о влиянии топологии магнитопровода на его приведенные характеристики, в области малых интенсивностей магнитных полей, сопоставимых с влиянием собственной намагниченности структуры, миокард сердца рассмотрен как совокупность магнитных доменов, которые связывают микроскопические магнитные характеристики с макроскопическими свойствами.
Разработан алгоритм анализа влияния топологии магнитопровода на распространение электромагнитного поля, и разработано, в среде прикладного программирования Delphi, программное средство для расчета, с учетом влияния топологии магнитопровода, распространение электромагнитного поля.
Показана качественная возможность характеристики функционального статуса миокарда по результатам измерения напряженности магнитного поля. Полученные значения показывают, что в качестве характеристики, позволяющей прогнозировать развитие патологий сердца, можно использовать параметр, характеризующий функциональный статус миокарда, а именно напряженность или индукцию магнитного поля, величина которой различается в зависимости от топологии магнитопровода до 3 раз.
Возможные области применения – выполнение оценки функционального резерва деятельности сердца.
Работа выполнена при поддержке гранта РФФИ № 14-07-00468.
Библиографическая ссылка
Арутюнов Ю.А., Возовиков И.Н., Митрофанов А.А., Чащин Е.А., Шеманаева Л.И., Живаев С.Н. ВЛИЯНИЕ ТОПОЛОГИИ ЛИСТА МЕБИУСА НА МАГНИТНЫЕ ХАРАКТЕРИСТИКИ ПОЛЯ ВНЕ МАГНИТОПРОВОДА // Современные наукоемкие технологии. – 2016. – № 7-1. – С. 9-14;URL: https://top-technologies.ru/ru/article/view?id=36053 (дата обращения: 19.04.2024).