Развивающаяся система городских пассажирских перевозок в России требует нового подхода к математическому моделированию взаимодействия участников транспортной системы. Существуют множества участников системы (включая пассажиров и транспортных операторов), имеющих несовпадающие интересы, которые приводят к конфликтным ситуациям, которые необходимо смоделировать.
Значение городского пассажирского транспорта (ГПТ) возрастает в условиях перехода экономики к рыночным механизмам функционирования, которые требуют применения новых методов исследования поведения поставщиков и потребителей товаров и услуг, так как именно ГПТ является основным способом перевозки пассажиров в пределах большинства российских городов.
Возрастание роли ГПТ прогнозируется также в США и странах Западной Европы. На долю ГПТ до сих пор приходится около 80 % общего объема перевозок всех видов транспорта России и около 25 % пассажирооборота [2].
Не привело к однозначным результатам начавшееся в последние десятилетия реформирование городского пассажирского транспорта. Привлечение на рынок пассажирских перевозок частных предпринимателей обеспечило переход городского пассажирского транспорта к рыночным отношениям. Положительной стороной этого стало сокращение времени ожидания на остановочных пунктах за счет все возрастающего количества подвижных единиц. При этом убытки муниципальных предприятий, осуществляющих перевозку пассажиров, увеличились (за счет сохранения льгот на проезд, движения по нерентабельным маршрутам и т.д.). В связи с этим требуется установить наиболее эффективный вариант работы различных участников рынка пассажирских перевозок, в том числе определить политику муниципальных органов власти с учетом интересов транспортных операторов и пассажиров.
Обилие интересов приводит к нуждаемости применения теории игр для моделирования поведения участников рынка городских пассажирских перевозок.
Жизнедеятельность городского пассажирского транспорта происходит в условиях ограничений. Изменения, которые произошли в России в 1990-е годы XX века, связаны еще и с тем, что государство не могло финансировать многие отрасли, в частности городской пассажирский транспорт. Муниципальный транспорт в России и большинстве других стран является убыточным, и не всегда бюджетных средств достаточно для покрытия убытков транспортных предприятий. Поэтому возникает задача оптимизации работы городского пассажирского транспорта в условиях ограничений на бюджетное финансирование. При заданном объеме финансирования фактически сводится задача к улучшению качества обслуживания пассажиров.
Нормативы по заполнению средства передвижения не всегда выполняются, но, с другой стороны, не каждый пассажир осуществит посадку в передвижное средство, у которого коэффициент наполнения около 1. Само понятие «заполнение» условное, например, в час пик коэффициент заполнения 0,73–0,78, а в иное время – не более 0,28. В такой ситуации появляется компромисс: у пассажира в час пик преобладает необходимость добраться до места назначения (например, места работы), смирившись с низким уровнем комфорта. Таким образом, заполнение передвижного средства для одних пассажиров может считаться критическим (высокие требования к комфорту), а другие готовы использовать любую возможность уехать и осуществляют посадку даже в переполненный автобус. Степень комфортабельности можно определить по тому, что предпочтет пассажир: отказаться от поездки общественным транспортом (в данном случае от многократных поездок) или использовать общественный транспорт для перемещений.
Моделирование поведения пассажиропотока на остановочном пункте
Рассмотрим в качестве примера функционирование остановочного пункта, через который проложено множество маршрутов. Необходимо определить, какая доля пассажиропотока будет использовать общественный транспорт, а какая откажется в связи с низким уровнем комфорта.
Для определения выбора способа перемещения введем следующие параметры:
K – количество маршрутов, способных перевезти пассажиропоток от данного остановочного пункта до места назначения;
λ – интенсивность пассажиропотока;
µ – общая интенсивность движения общественного транспорта, способного довезти пассажиропоток до конечного пункта;
Qk – средняя вместимость подвижного состава на маршруте k;
qk – среднее количество мест, занятых на транспортном средстве маршрута к, после выхода пассажиров на остановочном пункте;
рk – вероятность прихода к остановочному пункту транспортного маршрута k.
Движение транспорта и подход пассажиров к остановочному пункту является случайным процессом. Так как пассажиропоток могут перевезти несколько маршрутов, то общее распределение наполняемости подвижного состава получить сложно. Поэтому рассчитаем средний коэффициент этого показателя:
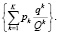
Чем выше значение у данного коэффициента, тем больше вероятность переполнения подвижного состава.
Введем следующий параметр: Cf – стоимостная оценка непримиримости пассажиров к тесноте. Данный параметр имеет денежную единицу измерения и используется при домножении на безразмерный показатель.
Также введем функцию «степени тесноты»:
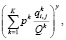
где y – некоторый параметр функции тесноты. Такая запись функции употребляется в литературе о транспорте [1] в интегральном критерии качества работы общественного транспорта.
Пассажир выражает недовольство, если приходят переполненные транспортные средства: чем выше заполнение, тем выше недовольство. Кроме того, введем следующие параметры: с – затраты на перемещение на легковом автомобиле; p – вероятность, что пассажиры выберут общественный транспорт для перемещения. Тогда 1 – p – вероятность того, что пассажиры выберут другой вид транспорта, например, легковой автомобиль. При этом пассажир заранее (или с течением времени, по накопленному опыту) определяет, какой способ перемещения он выберет.
Среднее количество пассажиров, ожидающих общественный транспорт:
.
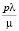При посадке пассажиров заполнение транспортного средства изменится. Для маршрута k коэффициент наполнения после посадки пассажиров составит:
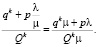
В таком случае предполагается, что все пассажиры воспользуются подошедшим транспортным средством. Потери пассажиров в связи с неудобством оценим следующим образом:
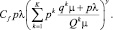
При этом перемещение на автомобиле считаем абсолютно комфортным по сравнению с общественным транспортом. С другой стороны, перемещение на легковом автомобиле является более затратным. Тогда критерий для пассажиропотока (потери, связанные с перемещением):
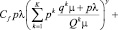
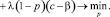(1)
Очевидно, что по параметру p при у ≥ 1функция (1) выпукла вверх.
Обобщение модели в городской среде
В городской среде существует множество маршрутов и остановочных пунктов, при обобщении маршрутной сети города используем следующую терминологию.
Первый вариант постановки задачи – без учета пересечения маршрутов. Основные параметры модели: Qk – максимальная номинальная вместимость транспортного средства; αk – стоимость одной ездки на k-м маршруте;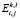 
– принимает значение 1, на k-м маршруте, если остановочный пункт l находится не позже пункта i и раньше пункта j, иначе принимает значение 0.
Кроме того, введем следующие параметры: ci,j – затраты на перемещение на легковом автомобиле между остановочными пунктами i и j; pi,j – вероятность того, что пассажир выберет общественный транспорт при перемещении между пунктами i и j; εi,j – ущерб городской среде от одного рейса легкового автомобиля между пунктами i и j.
Сначала оценим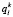 
– среднее количество пассажиров, находящихся в транспортном средстве маршрута k при подъезде к остановочному пункту l:
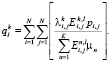
В данной формуле учтено, что не все пассажиры, осуществляя перемещение между некими пунктами, выбирают общественный транспорт.
Вероятность прихода транспортного средства маршрута k при перемещении пассажиропотока с остановочного пункта l до остановочного пункта m:
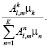
Средний коэффициент заполнения для пассажиропотока, перемещающегося между пунктами l и m:
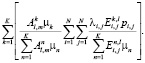
Тогда потери пассажиропотока составят:
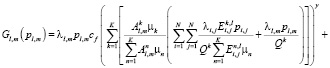
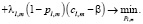(2)
Очевидно, что (2) выпукла вниз по pl,m при у > 1 (так как является произведением двух возрастающих выпуклых функций).
Далее рассчитаем потери системы «город», которые состоят из следующих составляющих:
1) потери в уютности при передвижении на городском пассажирском транспорте (из-за перезаполнения подвижного состава);
2) вред городской среде от эксплуатации городского пассажирского транспорта;
3) вред городской среде от эксплуатации легковых автомобилей.
Тогда потери системы «город» запишем в таком виде:
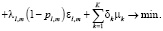(3)
Прибыль оператора, эксплуатирующего маршрут k:
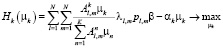. (4)
Между пассажиропотоками и транспортными операторами построим игру:
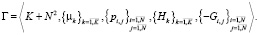
Утверждение 2. Игра пассажиропотоков и транспортных операторов
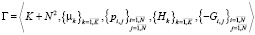
имеет ситуацию равновесия Нэша [2].
1. Условия теоремы существования ситуации равновесия рассмотрим по Нэшу.
Множество стратегий каждого игрока непусто, выпукло и компактно.
Очевидно, что множество стратегий пассажиропотоков между каждыми остановочными пунктами i и j непусто, выпукло и компактно – pi j [0, 1].
Очевидно, что интенсивность потоков транспортных средств, движущихся по каждому маршруту, не отрицательна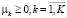 
и ограничена сверху экономической целесообразностью
,
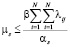данные ограничения обеспечивают выполнение условия для стратегий транспортных операторов.
2. Функция выигрыша каждого игрока непрерывна по стратегиям всех игроков и квазивогнута по собственным стратегиям.
Непрерывность обеспечивается видом функций выигрыша (2, 4).
Квазивогнутость обеспечивается более сильным утверждением – выпуклостью вверх. Функция потерь пассажиропотока (2) выпукла вниз при у > 0. Функция выигрыша транспортного оператора выпукла вверх.
Так как все условия теоремы выполнены, то в игре существует равновесие Нэша в чистых стратегиях.
Таким образом, потоки можно оптимально распределить по маршрутам общественного транспорта в случае повышенных требований пассажиропотоков к комфорту на транспорте.
Построена модель поведения пассажиров при посадке в транспортное средство на остановочном пункте. Главным показателем комфортабельности является коэффициент заполняемости передвижного средства. На его основе разработана целевая функция, позволяющая определить выбор пассажира между общественным транспортом и легковым автомобилем.
Библиографическая ссылка
Баламирзоев А.Г., Баламирзоева Э.Р., Гаджиева А.М. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДЕЙСТВИЯ ПАССАЖИРОПОТОКА ПРИ ЗАПОЛНЕНИИ СРЕДСТВА ПЕРЕДВИЖЕНИЯ // Современные наукоемкие технологии. – 2016. – № 2-3. – С. 407-410;URL: https://top-technologies.ru/ru/article/view?id=35642 (дата обращения: 25.04.2024).