Постановка задачи при упругих волновых воздействиях
Для решения двумерной плоской динамической задачи теории упругости с начальными и граничными условиями – используем метод конечных элементов в перемещениях. Постановки, численные методы, технология программных комплексов и анализ результатов решения нестационарных динамических задач для областей сложной формы рассмотрены в работах [1–10].
Разработка методики и алгоритма
Задача решается методом сквозного счета, без выделения разрывов. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений. Для решения линейных дифференциальных уравнений используем метод конечных элементов в перемещениях.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела Г, записываем приближенное значение уравнения движения в теории упругости
, 
, 
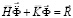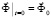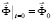,(1)
где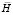 
– диагональная матрица инерции; 
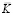– матрица жесткости; 
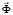– вектор узловых упругих перемещений; 
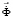– вектор узловых упругих скоростей перемещений; 
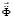– вектор узловых упругих ускорений; 
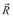– вектор внешних узловых упругих сил.
Интегрируя по временной координате соотношение (1) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную линейную схему в перемещениях для внутренних и граничных узловых точек
,
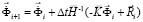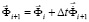. (2)
Общая теория численных уравнений математической физики требует для этого наложения определенных условий на отношение шагов по временной координате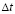 
и по пространственным координатам, а именно
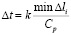
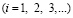, (3)
где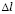 
– длина стороны конечного элемента.
Устойчивость двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних и граничных узловых точек на квазирегулярных сетках исследуем с помощью численного эксперимента. Результаты численного эксперимента показали, что при k = 0,5 обеспечивается устойчивость двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних и граничных узловых точек на квазирегулярных сетках.
На основе метода конечных элементов в перемещениях разработаны алгоритм и комплекс программ для решения линейных плоских двумерных задач, которые позволяют решать сложные задачи при нестационарных динамических воздействиях на уникальные сооружения. При разработке комплекса программ использовался алгоритмический язык Фортран-90.
В работах [2–10] приведена информация о численном моделировании волн напряжений.
Определение нестационарных упругих волн напряжений в подкрепленном круглом отверстии
Рассматривается задача о воздействии плоской продольной упругой волны на подкрепленное круглое отверстие. Начальные условия приняты нулевыми. В сечении на расстоянии 1,6H (рис. 1) при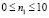 
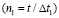скорость упругого перемещения 
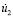изменяется линейно от 0 до 
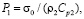а при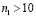 
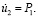Внутренний контур подкрепленного отверстия 
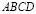предполагается свободным от нагрузок при 
.
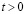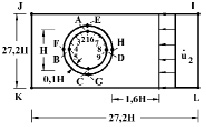
Рис. 1. Постановка задачи для подкрепленного круглого отверстия
На границе подкрепления и среды EFGH приняты условия непрерывности перемещений. Граничные условия для контура IJKL при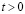 
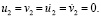Отраженные волны от контура IJKL не доходят до исследуемых точек при 
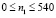. Расчеты проведены при следующих исходных данных:
Н = 0,2 м;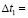 
0,186∙105 с; 
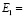0,72∙105 МПа (0,72∙106 кгс/см2); 
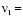0,3;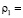 
0,275∙104 кг/м3 (0,275∙10-5 кгс∙с2/см4); 
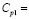5364 м/с; 
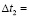0,407∙105 с; 
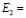0,36∙104 МПа (0,36∙105 кгс/см2); 
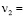0,36;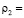 
0,122∙104 кг/м3 (0,122∙10-5 кгс∙с2/см4); 
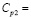1841 м/с; 
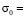–0,1 МПа (–1 кгс/см2) (
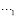– подкрепление; 
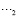– среда).
Исследуемая расчетная область имеет 1536 узловых точек. Внутренний контур подкрепления аппроксимирован 28 узловыми точками. По толщине подкрепление аппроксимировано двумя узловыми точками.
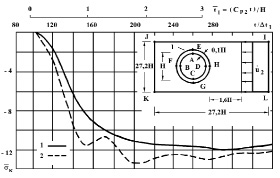
Рис. 2. Изменение упругого контурного напряжения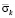 
в точке 1 во времени 
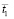на внутреннем контуре подкрепленного круглого отверстия при воздействии плоской продольной упругой волны типа функции Хевисайда
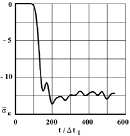
Рис. 3. Изменение упругого контурного напряжения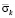 
в точке 1 на контуре подкрепленного круглого отверстия во времени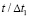 
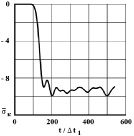
Рис. 4. Изменение упругого контурного напряжения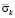 
в точке 2 на контуре подкрепленного круглого отверстия во времени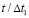 
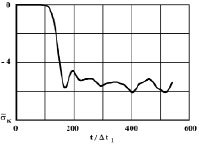
Рис. 5. Изменение упругого контурного напряжения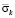 
в точке 3 на контуре подкрепленного круглого отверстия во времени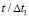 
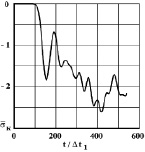
Рис. 6. Изменение упругого контурного напряжения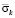 
в точке 4 на контуре подкрепленного круглого отверстия во времени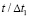 
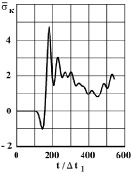
Рис. 7. Изменение упругого контурного напряжения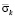 
в точке 5 на контуре подкрепленного круглого отверстия во времени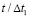 
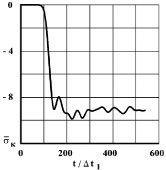
Рис. 8. Изменение упругого контурного напряжения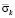 
в точке 6 на контуре подкрепленного круглого отверстия во времени 
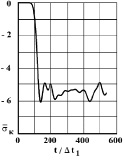
Рис. 9. Изменение упругого контурного напряжения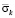 
в точке 7 на контуре подкрепленного круглого отверстия во времени 
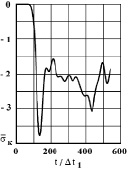
Рис. 10. Изменение упругого контурного напряжения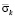 
в точке 8 на контуре подкрепленного круглого отверстия во времени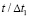 
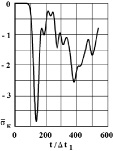
Рис. 11. Изменение упругого контурного напряжения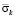 
в точке 9 на контуре подкрепленного круглого отверстия во времени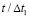 
На рис. 2 показано изменение контурного напряжения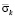 
в точке 1 во времени 
(
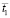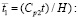1 – результаты аналитического решения [1]; 2 – результаты численного решения, полученные методом конечных элементов [2, 4 и 6]. Расхождение для максимального упругого контурного напряжения составляет 12 %. Результаты исследований показаны на рис. 3–11 в виде графиков изменения контурных напряжений 
(
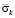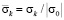) в точках 1–9 во времени 
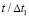при воздействии функции Хевисайда. Максимальной величины сжимающее контурное напряжение достигает в точке 1 почти за два прохода фронтом продольной волны диаметра среднего контура подкрепленного круглого отверстия и равно 
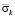= – 13,6.
Вывод
Сравнение с результатами аналитического метода показало их хорошее совпадение, что позволяет сделать заключение о физической достоверности результатов численного решения волновых задач.
Библиографическая ссылка
Мусаев В.К. ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ О РАСПРОСТРАНЕНИИ НЕСТАЦИОНАРНЫХ УПРУГИХ ВОЛН НАПРЯЖЕНИЙ В ПОДКРЕПЛЕННОМ КРУГЛОМ ОТВЕРСТИИ // Современные наукоемкие технологии. 2015. № 2. С. 93-97;URL: https://top-technologies.ru/ru/article/view?id=34897 (дата обращения: 26.04.2025).