Постановка динамической задачи теории упругости
Точные уравнения двумерной (плоское напряженное состояние) динамической теории упругости имеют вид
, 
,
,
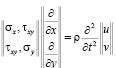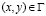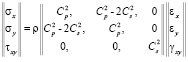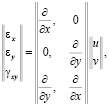
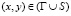, (1)
где 
, 
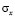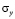и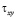 
– компоненты тензора упругих напряжени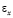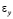й; 
, 
и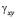 
– компоненты тензора упругих деформаци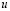й; 
и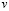 
– составляющие вектора упругих перемещений вдоль осей OX и OY соответственно; r – плотность материала; 
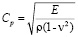– скорость продольной упругой волны; 
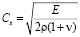– скорость поперечной упругой волны; n – коэффициент Пуассона; Е – модуль упругости; 
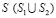– граничный контур тела Г.
Систему (1) в области, занимаемой телом Г, следует интегрировать при начальных и граничных условиях. Начальные условия в области Г зададим в виде
, 
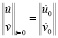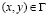, (2)
где 
, 
, 
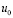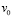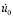и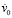 
– заданные в области Г функции.
Граничные условия зададим в виде:
составляющих компонентов тензора упругих напряжений на границе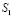 
, 
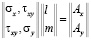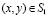; (3)
составляющих компонентов вектора упругих перемещений на границе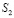 
, 
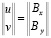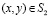, (4)
где l и m – направляющие косинусы;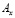 
, 
, 
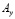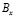и 
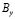– заданные на границе S функции.
Численное решение двумерной плоской динамической задачи теории упругости
Для решения двумерной плоской динамической задачи теории упругости с начальными и граничными условиями – используем метод конечных элементов в перемещениях.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела Г, записываем приближенное значение уравнения движения в теории упругости
, 
, 
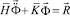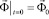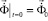, (5)
где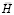 
– матрица инерции; 
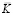– матрица жесткости; 
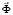– вектор узловых упругих перемещений; 
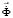– вектор узловых упругих скоростей перемещений; 
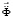– вектор узловых упругих ускорений; 
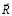– вектор узловых упругих внешних сил.
Интегрируя по временной координате соотношение (5) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек:
,
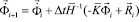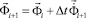. (6)
Основные соотношения метода конечных элементов в перемещениях получены с помощью принципа возможных перемещений и конечноэлементного варианта метода Галеркина. Система уравнений (5) для внутренних и граничных узловых точек, полученная в результате интегрирования уравнения движения теории упругости, должна давать решение, сходящееся к решению исходной системы (1). Шаг по временной переменной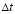 
определяем из следующего соотношения:
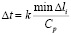
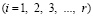, (7)
где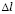 
– длина стороны конечного элемента.
Результаты численного эксперимента показали, что при k = 0,5 обеспечивается устойчивость двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних и граничных узловых точек на квазирегулярных сетках.
В работах [1–10] приводится информация о моделировании нестационарных волн напряжений в деформируемых телах.
Решение задачи о сосредоточенном взрывном воздействии
Рассмотрим задачу о сосредоточенном упругом взрывном воздействии (рис. 2) на набережной речного порта с незаполненным водным объектом (рис. 1). В работах [1, 3, 5, 9–10] приведена информация в области оценки достоверности результатов применяемого численного метода. В точке B приложено нормальное воздействие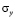 
, которое при 
(
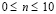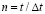) изменяется линейно от 
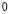до 
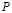, при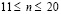 
изменяется P до 0 (
, 
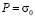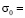– 0,1 МПа (–1 кгс/см2)). Граничные условия для контура CDEF при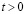 
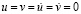. Отраженные волны от контура CDEF не доходят до исследуемых точек при 
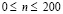. Контур CBAGF свободен от нагрузок, кроме точки 
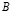, где приложено сосредоточенное воздействие. Расчеты проведены при следующих исходных данных: 
; 
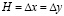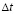= 1,393⋅10–6 с; E = 3,15⋅10 4 МПа (3,15⋅105 кгс/см2); n= 0,2; r= 0,255⋅104 кг/м3 (0,255⋅10-5 кгс с2/см4); Cp= 3587 м/с; Cs= 2269 м/с. Исследуемая расчетная область имеет 20402 узловые точки. Решается система уравнений из 81608 неизвестных.
На рис. 4–6 показано изменение упругого контурного напряжения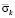 
(
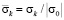) во времени n в точках A1–A3 (рис. 3), находящихся на свободной поверхности упругой полуплоскости. Растягивающее упругое контурное напряжение 
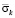от точки A1 до точки A10 изменяется от значения 
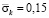до значения 
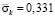. Сжимающее упругое контурное напряжение 
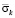от точки A1 до точки A10 изменяется от значения 
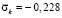до значения 
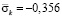. Растягивающее упругое нормальное напряжение 
(
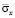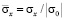) от точки 
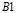до точки 
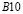изменяется от значения 
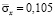до значения 
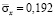. Сжимающее упругое напряжение 
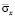от точки B1 до точки B10 изменяется от значения 
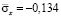до значения 
.
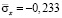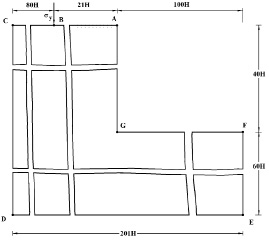
Рис. 1. Постановка задачи о сосредоточенном упругом взрывном воздействии на набережной речного порта с незаполненным водным объектом
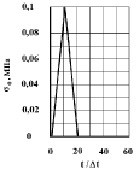
Рис. 2. Взрывное воздействие для задачи с незаполненным водным объектом
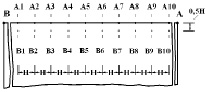
Рис. 3. Точки A1-A10 и B1-B10, в которых получены упругие напряжения во времени
Упругое нормальное напряжение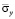 
в точках от точки B1 до точки B10 является очень маленьким. Растягивающее упругое нормальное напряжение 
(
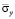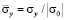) от точки 
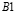до точки 
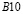изменяется от значения 
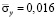до значения 
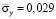. Сжимающее упругое напряжение 
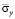от точки B1 до точки B10 изменяется от значения 
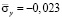до значения 
.
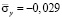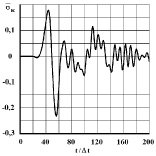
Рис. 4. Изменение упругого контурного напряжения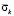 
во времени 
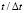в точке A1 в задаче с незаполненным водным объектом
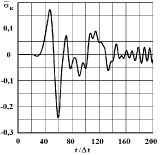
Рис. 5. Изменение упругого контурного напряжения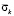 
во времени 
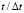в точке A2 в задаче с незаполненным водным объектом
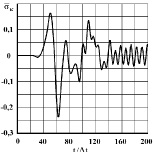
Рис. 6. Изменение упругого контурного напряжения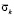 
во времени 
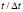в точке A3 в задаче с незаполненным водным объектом
Упругое касательное напряжение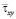 
в точках от точки B1 до точки B10 является маленьким. Растягивающее упругое касательное напряжение 
(
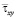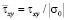) от точки B1 до точки B10 изменяется от значения 
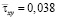до значения 
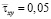. Сжимающее упругое касательное напряжение 
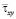от точки B1 до точки B10 изменяется от значения 
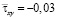до значения 
.
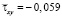Выводы
Для прогноза безопасности сооружений при взрывных воздействиях на набережной речного порта с водной средой применяется численное моделирование.
На основе метода конечных элементов в перемещениях разработаны методика, алгоритм и комплекс программ для решения линейных двумерных плоских задач, которые позволяют решать сложные задачи при взрывных воздействиях на сооружения. Задачи решаются методом сквозного счета, без выделения разрывов. Линейная динамическая задача с начальными и граничными условиями в виде дифференциальных уравнений в частных производных для решения задач при взрывных воздействиях с помощью метода конечных элементов в перемещениях приведена к системе линейных обыкновенных дифференциальных уравнений с начальными условиями, которая решается по явной двухслойной схеме.
Решена задача о сосредоточенном упругом взрывном воздействии на набережной речного порта с незаполненным водным объектом. Взрывное воздействие моделируется в виде треугольного импульса. Получены напряжения в точках на набережной речного порта с незаполненным водным объектом.
Библиографическая ссылка
Мусаев В.К. ОПРЕДЕЛЕНИЕ НЕСТАЦИОНАРНОГО НАПРЯЖЕННОГО СОСТОЯНИЯ ПРИ ВЕРТИКАЛЬНОМ СОСРЕДОТОЧЕННОМ ВЗРЫВНОМ ВОЗДЕЙСТВИИ НА НАБЕРЕЖНОЙ РЕЧНОГО ПОРТА С НЕЗАПОЛНЕННЫМ ВОДНЫМ ОБЪЕКТОМ // Современные наукоемкие технологии. – 2015. – № 2. – С. 88-92;URL: https://top-technologies.ru/ru/article/view?id=34896 (дата обращения: 21.11.2024).