В [1] были получены формулы, позволяющие рассчитывать межфазную энергию на границе раздела твердое тело – жидкость (расплав) σтж и поверхностную энергию твердого тела на границе раздела твердое тело – пар σтп по известным значениям краевого угла θ, образуемого жидкостью на поверхности твердого тела и поверхностной энергии жидкости на границе с паром σж
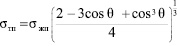 (1)
(1)
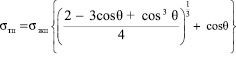 (2)
(2)
Формулы (1) и (2) получены строго термодинамическим методом, поэтому они применимы к равновесным системам любой природы, в частности, в тех случаях, когда смачивание не сопровождается химической реакцией.
В настоящей работе проведены вычисления σтж и σтп и работы адгезии WA некоторых полимеров при их смачивании водными растворами спиртов. Экспериментальные значения σжп и θ заимствованы из [2]. Результаты расчетов σтж, σтп и WA приведены в табл. 1. Отметим, что исследованные системы характеризуются отсутствием химических взаимодействий.
Таблица 1
|
Полимер-раствор |
С, моль/л |
θ, град |
σжп, |
σтж, |
σтп, |
WA, |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
ПФ-метанол |
0,5 1,0 3,0 5,0 |
107 104 100 93 |
69,1 65,7 56,9 51,1 |
61,7 57,7 48,8 41,6 |
41,5 41,8 38,9 38,9 |
48,9 49,8 47,0 48,4 |
|
ПТФЭ – метанол |
0,5 1,0 3,0 5,0 |
116 115 110 107 |
69,1 65,7 56,9 51,1 |
64,4 60,9 51,6 45,6 |
34,1 33,2 32,2 30,7 |
38,8 38,0 37,5 36,2 |
Окнчание табл. 1
|
ПП-метанол |
0,5 1,0 3,0 5,0 |
87 85 79 73 |
69,1 65,7 56,9 51,1 |
53,4 49,8 40,4 33,7 |
57,0 55,5 51,3 48,6 |
72,7 71,4 67,8 66,0 |
|
ПК-метанол |
0,5 1,0 3,0 5,0 |
86 84 77 71 |
69,1 65,7 56,9 51,1 |
52,9 49,8 39,5 32,8 |
57,7 56,1 52,3 49,4 |
73,9 72,0 69,7 67,7 |
|
ПФ-этанол |
0,5 1,0 2,0 4,0 |
105 100 94 84 |
64,0 58,7 51,8 43,0 |
56,6 50,3 42,5 32,2 |
40,0 40,1 38,9 36,8 |
47,4 48,5 48,2 47,6 |
|
ПТФЭ-этанол |
0,5 1,0 2,0 4,0 |
119 116 112 102 |
64,0 58,7 51,8 43,0 |
60,3 54,7 47,4 37,3 |
29,2 28,9 28,0 28,4 |
32,9 32,9 32,4 34,1 |
|
ПП-этанол |
0,5 1,0 2,0 4,0 |
86 81 76 64 |
64,0 58,7 51,8 43,0 |
49,0 42,6 35,5 24,8 |
53,4 51,8 48,0 43,7 |
68,4 67,9 64,3 61,9 |
|
ПК-этанол |
0,5 1,0 2,0 4,0 |
84 80 75 65 |
64,0 58,7 51,8 43, |
48,0 42,2 35,1 25,2 |
54,7 52,4 48,5 43,4 |
70,7 68,9 65,2 61,2 |
|
ПФ-пропанол |
0,1 0,3 1,0 2,0 |
105 98 85 67 |
65,7 57,3 43,7 34,5 |
58,0 48,4 33,1 20,9 |
41,0 40,4 36,9 34,4 |
48,7 49,3 47,5 48,0 |
|
ПТФЭ-пропанол |
0,1 0,3 1,0 2,0 |
119 112 97 83 |
65,7 57,3 43,7 34,5 |
61,9 52,5 36,7 25,6 |
30,0 31,0 31,4 29,8 |
33,8 35,8 38,4 38,7 |
|
ПП-пропанол |
0,1 0,3 1,0 2,0 |
87 80 66 47 |
65,7 57,3 43,7 34,5 |
50,8 41,2 26,0 14,1 |
54,2 51,1 43,8 37,6 |
69,1 67,2 61,5 58,0 |
|
ПК-пропанол |
0,1 0,3 1,0 2,0 |
86 78 66 52 |
65,7 57,3 43,7 34,5 |
50,3 40,2 26,0 15,8 |
54,8 52,2 43,8 37,1 |
70,2 69,3 61,5 55,8 |
|
ПФ-бутанол |
0,05 0,1 0,3 0,5 |
103 97 84 72 |
62,2 56,1 43,3 36,5 |
54,3 47,1 32,5 23,8 |
40,3 40,2 37,0 35,0 |
48,2 49,2 47,8 47,7 |
|
ПТФЭ-бутанол |
0,05 0,1 0,3 0,5 |
117 112 98 86 |
62,2 56,1 43,3 36,5 |
58,2 51,4 36,6 27,9 |
29,9 30,4 30,6 30,5 |
33,9 35,1 37,3 39,1 |
|
ПП-бутанол |
0,05 0,1 0,3 0,5 |
84 78 65 52 |
62,2 56,1 43,3 36,5 |
46,6 39,4 25,4 16,8 |
53,2 51,1 43,7 39,2 |
68,8 67,8 61,6 58,9 |
|
ПК-бутанол |
0,05 0,1 0,3 0,5 |
82 77 64 53 |
62,2 56,1 43,3 36,5 |
45,7 38,9 25,0 17,1 |
54,3 51,6 44,0 39,1 |
70,8 68,8 62,3 58,5 |
Сокращенные названия полимеров в табл. 1 означают: ПФ – парафин; ПТФЭ – политетрафторэтилен; ПП – полипропилен; ПК – поликарбонат.
Температура для всех систем t = 25°С.
При расчетах десятые доли значений краевых углов нами были предварительно округлены до целых.
Анализ полученных данных показывает, что с увеличением концентрации спиртов в воде σтж и σтп уменьшаются. Такое поведение указанных величин находится в соответствии с критериями смачиваемости твердых тел жидкостями и поверхностной активности в бинарных растворах. Из табл. 1 видно, что при σтж > σтп краевой угол q всегда больше 90°, а при σтж < σтп, q всегда меньше 90°.
Из табл. 1 также ви, в зависимости от соотношений между σтж, σтп и σжп:
σтж < σтп ≤ σжп, q < 90°, (3)
σтж > σтп < σжп, q > 90°. (4)
Соотношения (3) и (4) выполняются всегда для однокомпонентных и разнородных жидкостей и твердых тел, находящихся в термодинамическом равновесии, при любом виде взаимодействий. Прежде чем применять выражения (1) и (2) к разнородным системам, необходимо предварительно определить σтп для однокомпонентного твердого тела или любого другого тела (не разлагающегося при плавлении), используя те же формулы (1) и (2), а затем по найденному значению σтп вычислить межфазную энергию данного тела на границах с несобственными расплавами σтж по формуле Юнга. К сожалению, экспериментальное определение θ для границы твердое тело – собственный расплав связано с большими трудностями, поэтому к настоящему времени θ измерены только для некоторых органических, неорганических, нескольких полупроводников и металлов. С другой стороны, из формул (1) и (2) следует, что при θ ≈ 0°, σтж = 0, следовательно σтп = σжп (условие минимума σтж). Равенство нулю σтж при q = 0° свидетельствует о том, что краевой угол q твердого тела собственным расплавом не равен нулю (ранее считалось, что этот угол смачивания θ = 0).
Наши расчеты по формулам (1) и (2) показали, что на границе твердого тела со своим расплавом при изменении θ от 1° до 36°, σтп растет до максимального значения σтп = 1,103797 σжп (условие максимума σтп), а затем убывает с ростом θ и становится равной поверхностной энергии жидкости (расплава) σжп при θ = 66 – 67°. По достижению краевого угла 90°, σтп = σтж = 0,793701 σжп. Как отмечено выше, θ > 90°, σтж > σтп и при θ = 180°, σтп равнялась бы нулю, если бы в природе существовало твердое тело с нулевой поверхностной энергией. Отсюда следует, что реально θ всегда меньше 180°. Как показали опыты максимальное значение θ ≤ 165°. Следовательно, θ = 180° недостижим, поэтому σтп также не равна нулю для любой системы. При этом, адгезия также равнялась бы нулю, что также невозможно.
При расчетах межфазных характеристик для жидкостей и поликристаллических твердых тел в качестве σтп, по-видимому, можно взять усредненное значение σтп = 1,0518985 σжп (если отсутствуют измеренные значения краевых углов, образуемых собственными расплавами (жидкостями) на поверхностях твердых тел). При наличии краевых углов в зависимости от ориентации граней кристаллов θ (hkl), можно определять также σтж (hkl) и σтп (hkl).
В заключение отметим, что формулы (1) и (2) выведены нами термодинамически, поэтому они будут справедливыми для любых типов систем и позволят рассчитать приближенно межфазные характеристики по известным из литературы значениям θ и σжп.
Точность расчетов зависит от точности экспериментальных данных θ и σжп. С учетом всех возможных ошибок относительная ошибка нами оценена в 2 %.
В заключение еще раз отметим, что при необходимости точность можно улучшить, если провести расчеты без округления значений краевых углов до целых величин.
Библиографическая ссылка
Дохов М.П., Кокоева М.Н. МЕЖФАЗНЫЕ ЭНЕРГИИ НЕКОТОРЫХ ПОЛИМЕРОВ НА ГРАНИЦЕ С ВОДНЫМИ РАСТВОРАМИ СПИРТОВ // Современные наукоемкие технологии. 2014. № 9. С. 64-66;URL: https://top-technologies.ru/ru/article/view?id=34707 (дата обращения: 01.07.2025).



