Выведенное знаменитым французским математиком П. Ферма (1601-1665) каноническое уравнение окружности представляет широкий научный интерес в практическом приложении, так как часто применяется при вычислении различных задач экономического содержания.
В уравнении окружности содержатся основные сведения об этой фигуре, например, координаты её центра или длина радиуса. Это является необходимой информацией для построения данной геометрической фигуры. В других задачах, наоборот, условием является составление уравнения по исходным параметрам.
Приложение уравнения окружности к решению экономических задач отражает взаимосвязь аналитической геометрии и экономики.
Окружностью называют геометрическое место точек (множество всех точек) на плоскости, равноудаленных от одной точки, называемой центром. Расстояние от центра до любой точки окружности называется радиусом.
Каноническое уравнение окружности имеет вид:
.
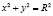Также существует нормальное уравнение окружности:
,
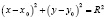где С – центр окружности, а R – радиус.
Являясь кривой второго порядка, окружность удовлетворяет данному уравнению:
,
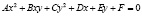где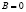 
, 
.
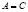Мы может точно сказать, что действительная кривая второго порядка является окружностью тогда и только тогда, когда:
1) коэффициенты при квадратах текущих координат равны между собой;
2) отсутствует член, содержащий произведение текущих координат.
Остановимся на рассмотрении примера решения экономической задачи с использованием канонического уравнения окружности:
Два предприятия A и B, расстояние между которыми равно 200 км, производят некоторое изделие, заводская цена (руб.) которого одна и та же для обоих предприятий. Транспортные расходы на перевозку единицы изделия от предприятия A до потребителя P составляют 9 руб./км, а от предприятия B – 3 руб/км. Как следует разделить рынок сбыта, чтобы расходы потребителей были одинаковыми? Какому потребителю изделия, какого предприятия выгоднее покупать?
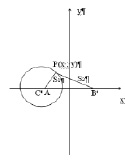
Решение данной задачи сводится, во-первых, к наглядному построению прямоугольной системы координат поместив начало координат в середине отрезка AB и направив ось абсцисс по лучу AB, а ось ординат перпендикулярно ему. Определим геометрическое место точек, в которых расходы потребителей на приобретение продукции предприятий A и B будут одинаковыми. Допустим, что потребитель располагается в точке P с координатами (x,y). Тогда обозначим расстояния от точки P до точек A и B как расстояние равное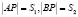 
(км).
В таком случае расходы на приобретение единицы изделия предприятия A будут равны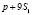 
, а предприятия B – 
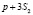. По условию расходы потребителей должны быть одинаковыми, то <
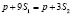. Преобразовав, получим, что
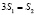. (1)
Вычислим значения S1 и S2, используя координаты точек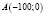 
, 
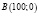и P(x,y):
.
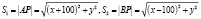Затем подставив в равенство (1) будем иметь:
.
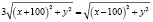Отсюда получим уравнение:
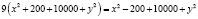
или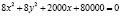 
.
Разделим обе части уравнения на 8, сгруппируем его члены по переменным и дополним до полного квадрата скобки. Тогда уравнение примет вид: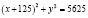 
.
Конечное уравнение есть уравнение окружности, с центром в точке C, которая имеет координаты (–125;0), и радиусом R=75.
Для потребителей, находящихся на этой окружности,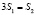 
, значит, 
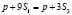, расходы на приобретение изделия, как предприятия A, так и предприятия B одинаковы. Для потребителей, находящихся внутри круга, который ограничен данной окружностью, 
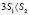, следовательно, 
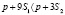, поэтому расходы на приобретение изделий предприятия A ниже. Также можно установить, что для потребителей, находящихся вне этого круга, ниже расходы на приобретение изделий предприятия B.
Таким образом, рынок сбыта можно выгодно распределить на несколько экономичных частей таким образом: а) потребителям, находящимся на окружности, безразлично, изделия каких предприятий покупать; б) потребители, находящиеся внутри указанного круга, покупают изделия предприятия A; в) потребители, находящиеся вне круга, покупают изделия предприятия B.
В заключение хотелось бы отметить, что для решения многих задач экономического профиля требуются математическая подготовка и знание теоретического материала. Следовательно, зная уравнение окружности, можно произвести анализ рынка сбыта и исследовать поведение потребителей (покупателей). Установить более выгодные продажи потребительского характера, а пользуясь в процессе решения формулой канонического уравнения окружности и некоторые из наиболее выгодных способов получения прибыли.
Библиографическая ссылка
Дедкова Д.Е., Родина Е.В. ИСПОЛЬЗОВАНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ ОКРУЖНОСТИ В РЕШЕНИИ ЭКОНОМИЧЕСКИХ ЗАДАЧ // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 152-153;URL: https://top-technologies.ru/ru/article/view?id=34035 (дата обращения: 18.04.2024).