Согласно проведенным исследованиям делителем нуля 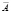 некоторой заданной матрицы A называется такая матрица, произведение которой с матрицей A тождественно равно нулю. Механизм действия делителей нуля основан на использовании линейной зависимости столбцов (правый делитель) и строк (левый делитель) матрицы A.
некоторой заданной матрицы A называется такая матрица, произведение которой с матрицей A тождественно равно нулю. Механизм действия делителей нуля основан на использовании линейной зависимости столбцов (правый делитель) и строк (левый делитель) матрицы A.
Матрица A размера (m×n) имеет правый делитель нуля, если можно подобрать такую другую матрицу 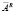 , содержащую n строк и произвольное число q столбцов, что всегда выполняются тождество и два неравенства
, содержащую n строк и произвольное число q столбцов, что всегда выполняются тождество и два неравенства
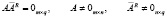
где 0i×k – нулевая матрица размера (i×k).
Итак, нулевое значение произведения матриц 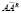 обусловлено тем, что используются соответствующие комбинации только линейно зависимых столбцов. Если матрица A не содержит линейно зависимых столбцов, то у нее не может быть правого делителя нуля. У матрицы, имеющей только линейно независимые столбцы, правый делитель нуля равен нулевой матрице (нулю).
обусловлено тем, что используются соответствующие комбинации только линейно зависимых столбцов. Если матрица A не содержит линейно зависимых столбцов, то у нее не может быть правого делителя нуля. У матрицы, имеющей только линейно независимые столбцы, правый делитель нуля равен нулевой матрице (нулю).
Правый делитель нуля может содержать неограниченное число столбцов, т.е. неограниченное число вариантов комбинирования линейно зависимых столбцов матрицы A. В то же время для n столбцов этой матрицы могут существовать только 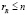 их линейно независимых комбинаций, тождественно равных нулю. Крайний случай
их линейно независимых комбинаций, тождественно равных нулю. Крайний случай 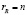 соответствует матрице A, все столбы которой нулевые. Если у матрицы есть хотя бы один ненулевой столбец, то
соответствует матрице A, все столбы которой нулевые. Если у матрицы есть хотя бы один ненулевой столбец, то 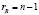 и т.д. В общем случае число rR равно размерности ядра оператора F.
и т.д. В общем случае число rR равно размерности ядра оператора F.
В дальнейшем будем полагать, что для матрицы A правый делитель нуля 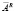 имеет размер
имеет размер 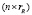 и максимальный, т.е. равный
и максимальный, т.е. равный 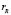 , ранг. В таком случае охватывается все возможные линейно независимые конструкции, а значит и вообще все возможные конструкции соответствующих делителей нуля.
, ранг. В таком случае охватывается все возможные линейно независимые конструкции, а значит и вообще все возможные конструкции соответствующих делителей нуля.
Если у матрицы A имеется левый делитель нуля, значит можно подобрать такую другую матрицу 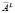 размера
размера 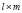 , что всегда выполняется
, что всегда выполняется
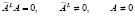
Левый делитель нуля оперирует со строками матрицы A. Из m строк матрицы A могут быть составлены не более 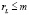 линейно независимых комбинаций, тождественно равных нулю. Соответственно
линейно независимых комбинаций, тождественно равных нулю. Соответственно 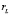 – размерность левого нуль-пространства отображения, задаваемого матрицей A, размерность коядра оператора F. Для определенности также будем полагать, что левый делитель нуля имеет размер
– размерность левого нуль-пространства отображения, задаваемого матрицей A, размерность коядра оператора F. Для определенности также будем полагать, что левый делитель нуля имеет размер 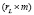 и максимальный ранг
и максимальный ранг 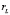 .
.
Левые матричные делители нуля обладают следующими свойствами:
|
транспонирование |
|
|
умножение на обратимую матрицу S |
если |
|
умножение на произвольную матрицу p |
|
|
нильпотентная конструкция матриц индекса 2 с произвольной матрицей k |
|
|
делители нуля произведения матриц с сохранением ранга |
если |
|
делители нуля произведения матриц с понижением ранга |
если |
|
обратимость сводной матрицы |
если |
Правые матричные делители нуля обладают следующими свойствами:
|
транспонирование |
|
|
умножение на обратимую матрицу S |
если |
|
умножение на произвольную матрицу m |
|
|
нильпотентная конструкция матриц индекса 2 с произвольной матрицей h |
|
|
делители нуля произведения матриц с сохранением ранга |
если |
|
делители нуля произведения матриц с понижением ранга |
если |
|
обратимость сводной матрицы |
если |
Первые три свойства очевидны и проверяются непосредственным вычислением, например,
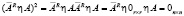
Свойства «c» предоставляют возможность при формировании делителей нуля без ущерба для общности результата в качестве ненулевых элементов записывать различные фиксированные числа, например единицы. Произвольность матричных множителей p и m с любым (подходящим по контексту) числом строк и столбцов соответственно порождает всю совокупность элементов класса. Можно сказать и иначе. Для левого матричного делителя нуля максимального ранга: линейные комбинации его строк порождают все другие левые матричные делители нуля. Для правого матричного делителя нуля максимального ранга: линейные комбинации его столбцов порождают все другие правые матричные делители нуля.
Свойства «e», «f» вытекают из определения ядра и коядра. Ядро отображения, задаваемого матрицей 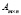 , имеет размерность
, имеет размерность 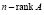 , в то же время, ядро произведения матриц BA имеет размерность
, в то же время, ядро произведения матриц BA имеет размерность 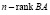 . В соответствии с неравенством Сильвестра ранг произведения матриц не может превышать рангов сомножителей. Таким образом, в случае совпадения рангов (свойство «e») непосредственно из формул произведения AB и BA видно, что все делители нуля матрицы A будут таковыми для произведения матриц и наоборот. В противном случае (свойство «f») у произведения матриц AB и BA в связи с понижением ранга у делителей нуля
. В соответствии с неравенством Сильвестра ранг произведения матриц не может превышать рангов сомножителей. Таким образом, в случае совпадения рангов (свойство «e») непосредственно из формул произведения AB и BA видно, что все делители нуля матрицы A будут таковыми для произведения матриц и наоборот. В противном случае (свойство «f») у произведения матриц AB и BA в связи с понижением ранга у делителей нуля 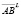 и
и 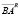 возникают дополнительные по сравнению с делителями
возникают дополнительные по сравнению с делителями 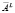 и
и 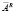 строки и столбцы соответственно.
строки и столбцы соответственно.
Свойство «g» связано со следующим. Во-первых, число линейно независимых строк левого делителя нуля (столбцов правого делителя нуля) прямоугольной матрицы всегда дополняет число столбцов (строк) этой матрицы до числа строк (столбцов). Во-вторых, строки левого делителя (столбцы правого делителя) такой матрицы и строки (столбцы) самой матрицы всегда в совокупности линейно независимы.
Далее, если у прямоугольной матрицы C существует правый делитель нуля 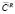 , тогда независимо от числа столбцов
, тогда независимо от числа столбцов 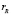 этого делителя имеет место лемма об обращении
этого делителя имеет место лемма об обращении 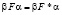
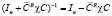
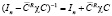
где c – произвольная матрица соответствующего размера.
Рассмотрим сейчас структуру делителей нуля.
Если определение делителей нуля для исходной матрицы A представляет собой непростую задачу, то для матриц в канонических базисах структуры делителей нуля очевидны. Действительно, матрицы
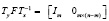 ,
, 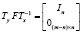
содержат блоки только двух типов: единичные и нулевые. Ясно, что все строки и столбцы этих матриц, пересекающие единичные блоки, линейно независимы между собой. Таким строкам и столбцам в делителях нуля должны соответствовать нулевые строки и столбцы. В то же время строки и столбцы, пересекающие нулевые блоки, содержат только нулевые элементы и поэтому всегда линейно зависимы. Именно эти нулевые строки и столбцы матриц в канонических базисах используются для формирования делителей нуля.
В силу сказанного для матриц изоморфизмов делители нуля не существуют, точнее, существуют только нулевые делители нуля.
Эпиморфная матрица 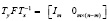 в канонических базисах не содержит ни одной нулевой строки, но имеет
в канонических базисах не содержит ни одной нулевой строки, но имеет 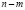 нулевых столбцов. Таким образом, у эпиморфизмов отсутствуют левые делители нуля, но могут быть сформированы правые делители нуля, использующие
нулевых столбцов. Таким образом, у эпиморфизмов отсутствуют левые делители нуля, но могут быть сформированы правые делители нуля, использующие 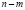 нулевых столбцов, которые по определению линейно зависимы, или столько же их линейных комбинаций.
нулевых столбцов, которые по определению линейно зависимы, или столько же их линейных комбинаций.
Правый канонический делитель нуля максимального ранга для матрицы 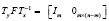 с простейшей (канонической) структурой имеет вид
с простейшей (канонической) структурой имеет вид
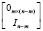 .
.
Этот делитель имеет 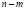 линейно независимых столбцов (единичный блок) и m нулевых строк.
линейно независимых столбцов (единичный блок) и m нулевых строк.
По аналогии можно придти к выводу, что мономорфизмы с матрицами в канонических базисах
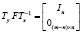
не имеют правых делителей нуля, а их канонические левые делители нуля представлены матрицами вида
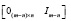
Здесь делитель нуля имеет ранг 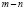 , и именно столько линейно независимых комбинаций строк матрицы A могут дать нулевые значения.
, и именно столько линейно независимых комбинаций строк матрицы A могут дать нулевые значения.
Для общего (гомоморфного) случая
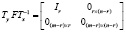
характерно наличие левых и правых делителей нуля одновременно. Им соответствуют следующие канонические записи: для правых делителей нуля
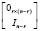
и для левых делителей нуля
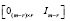
Число возможных линейно независимых комбинаций столбцов матрицы A, имеющих нулевые значения, согласно 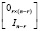 равно
равно 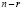 , а строк – согласно
, а строк – согласно 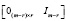 равно
равно 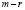 .
.
Обратим внимание на делители нуля матрицы-строки и матрицы-столбца. По определению эти оба типа матриц имеют максимальный ранг, равный единице. Отсюда следует, что у матрицы-строки нет левых делителей нуля, но она всегда имеет правый делитель нуля вида 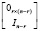 , размера
, размера 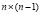 и ранга
и ранга 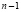 . Матрица-столбец напротив не имеет правых делителей нуля и всегда имеет левый делитель нуля вида
. Матрица-столбец напротив не имеет правых делителей нуля и всегда имеет левый делитель нуля вида 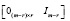 , размера
, размера 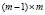 и ранга
и ранга 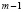 .
.
Теперь можно вернуться к проблеме выборочной эквивалентности.
Пусть у матрицы a, соответствующей оператору A, существует левый делитель нуля 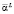 , а у матрицы b, соответствующей оператору B, – правый делитель нуля
, а у матрицы b, соответствующей оператору B, – правый делитель нуля 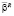 , тогда согласно свойству «c» из
, тогда согласно свойству «c» из 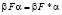 вытекает тождество
вытекает тождество
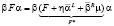 ,
,
где h и m – произвольные матрицы соответствующих размеров. В то же время не вызывает сомнения неравенство
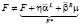 .
.
Таким образом, выборочная эквивалентность систем
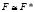
не предполагает их полной эквивалентности. И только при условии 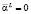 и
и 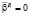 справедливо тождество
справедливо тождество 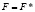 , а выборочная эквивалентность совпадает с полной эквивалентностью.
, а выборочная эквивалентность совпадает с полной эквивалентностью.
Библиографическая ссылка
Гулай Т.А., Семенов Д.В., Кудрина Ю.Г. ДЕЛИТЕЛИ НУЛЯ, СТРУКТУРЫ ДЕЛИТЕЛИ НУЛЯ И ВЫБОРОЧНАЯ ЭКВИВАЛЕНТНОСТЬ СИСТЕМ // Современные наукоемкие технологии. 2014. № 5-2. С. 148-150;URL: https://top-technologies.ru/ru/article/view?id=34032 (дата обращения: 02.07.2025).




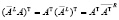 ,
,
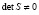 , то
, то 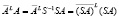 ,
,
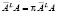 ,
, 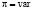 ,
,
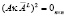 ,
, 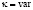 ,
,
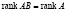 , то
, то 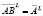 ,
,
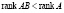 , то
, то 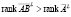
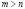 и
и 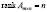 , то
, то 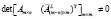
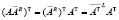 ,
,
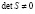 , то
, то 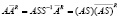 ,
,
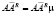 ,
, 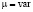 ,
,
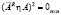 ,
, 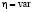 ,
,
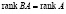 , то
, то 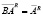 ,
,
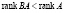 , то
, то 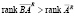
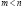 и
и 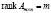 , то
, то 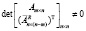 .
.