В полной мере теория приложений может быть разработана с применением кратных, криволинейных и поверхностных интегралов. Поэтому в нашей статье нецелесообразно превышать некоторый уровень математической строгости. Навыки работы в этом направлении – вот что будет для нас главным в нашей статье.
Рассмотрим вычисление площадей плоских фигур. Площадь криволинейной фигуры может быть найдена из уже известного геометрического смысла определенного интеграла (рис. 1).
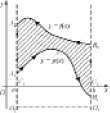
Рис. 1
.
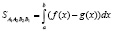Для дальнейших приложений это будет удобно записать в виде криволинейного интеграла (все связанное с криволинейным интегралом, пока следует рассматривать только как удобную форму записи).
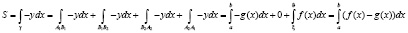
Для областей с конфигурацией как на рис. 2 более удобной является формула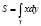 
.
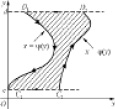
Рис. 2
При обходе областей сложной конфигурации можно разбивать ее на более простые области (пример указан на рис. 3) и для вычисления площадей плоских фигур пользоваться либо формулой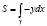 
, либо формулой 
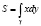, либо комбинированной формулой:
.
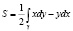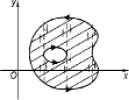
Рис. 3
Если функция, определяющая границу области, задана параметрически
,
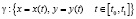то последняя формула принимает вид:
.
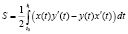Формула для нахождения площади фигуры, граница которой задана в полярных координатах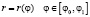 
, имеет вид: 
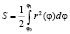и получена суммированием площадей элементарных криволинейных треугольников 
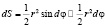(рис. 4б, см. пункт 2).
Рассмотрим вычисление длин дуг плоских кривых. Формула для нахождения длина дуги кривой получается суммированием длин элементарных дуг. Длина элементарной дуги в декартовых координатах может быть найдена по формуле Пифагора (рис. 4а):
.
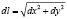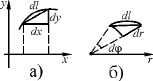
Рис. 4
а) Если кривая задана явно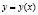 
, то 
;
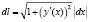б) Если же кривая задана явн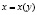о 
, то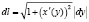 
;
в) Для кривой, заданной параметрически,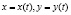 
, получим
.
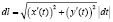г) В полярной системе координат (рис. б)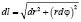 
. В различных частных случаях:
.
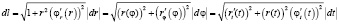д) формула для нахождения длины дуги кривой, записанная через криволинейный интеграл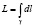 
. Данная формула, с учетом способа задания кривой, может быть переписана с помощью интеграла Римана, например:
.
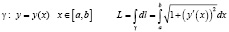Пример. Найти площадь и длину дуги эллипса с полуосями а и b.
Зададим эллипс параметрическим уравнением: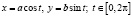 
. Тогда
1) 
.
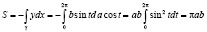2) 
=
=
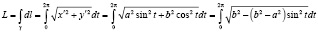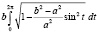
Получившийся интеграл – эллиптический интеграл и не выражается через элементарные функции. Его значение может быть найдено численными методами, например, методом прямоугольников, трапеций или Симпсона. Также его значение может быть найдено в справочниках по специальным функциям (например, М. Абрамович, И. Стиган).
Рассмотрим криволинейные интегралы I-го рода.
Для кривой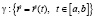 
определим
.
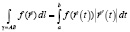Так, определенный интеграл называется криволинейным интегралом первого рода.
Физический смысл криволинейного интеграла первого рода: если функция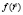 
определяет линейную плотность масс на кривой, то 
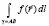определяет массу кривой.
Рассмотрим вычисление площадей поверхностей вращения и вычисление объёмов.
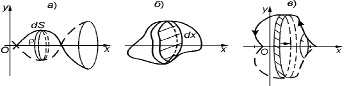
Рис. 5
На рисунках проиллюстрированы формулы:
а) для нахождения объема тела, полученного вращением плоской кривой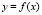 
вокруг оси Ox:
;
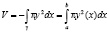б) для нахождения объёма тела с известной площадью поперечного сечения:
;
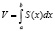в) для нахождения площади поверхности тела, полученного вращением плоской кривой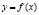 
вокруг оси Ox:
.
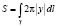Рассмотрим вычисление моментов и координат центра масс. Статический момент конечной системы материальных точек с массами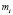 
и радиус-векторами 
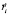находится по формуле
.
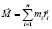Радиус-вектор центра масс будет равен
,
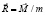где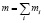 
.
Тогда, если (x, y, z) – декартовы координаты, а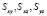 
– статические моменты системы материальных точек относительно координатных плоскостей 
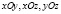соответственно, то 
, 
, 
.
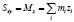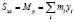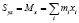А для координат центра масс имеем:
; 
; 
.
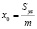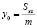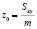Для точек, лежащих в одной плоскости с декартовыми координатами (x, y), если обозначить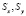 
статические моменты относительно осей Ox и Oy, получим формулы:
; 
.
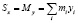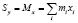И для центра масс, соответственно
; 
.
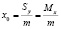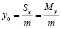Для системы точек, лежащих в плоскости можно говорить и о моментах kго порядка:
, 
.
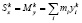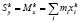При этом очевидно, что масса системы точек это момент нулевого порядка, а статические моменты это моменты первого порядка. Моменты второго порядка называются моментами инерции.
Момент инерции системы материальных точек относительно некоторой оси определяется равенством
,
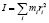где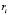 
– расстояния от точек системы до соответствующих осей.
При применении определенного интеграла к вычислению моментов тела разбиваются на тонкие слои из точек «равноудаленных» от соответствующих плоскостей (или осей), и каждый такой слой рассматривается как единое целое.
Пример. Найти статический момент эллипса относительно касательной к эллипсу в его «вершине», если эллипс однороден (плотностью ρ).
Уравнение эллипса: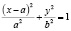 
(рис. 6б).
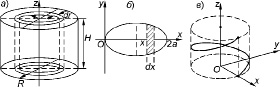
Рис. 6
Разрежем эллипс на элементарные полоски параллельные оси ординат. Так как полоски достаточно узкие, можно считать, что все точки элементарной полоски находятся на одинаковом расстоянии x от оси ординат. Площадь элементарной полоски, в таком предположении, равна
.
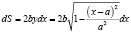Умножая площадь на плотность, получим массу элементарной полоски
.
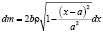Расстояние от элементарной полости до оси Oy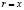 
.
Тогда для статического момента эллиптической пластинки относительно прямой, проходящей через его вершину, параллельно одной из осей (в нашем случае – оси ординат), получаем:
.
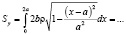При этом плотность может даже зависеть от х: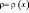 
.
Библиографическая ссылка
Бондаренко В.А., Ханларов С.Т. ПРИМЕНЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА В ГЕОМЕТРИЧЕСКИХ И ФИЗИЧЕСКИХ ЗАДАЧАХ // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 143-146;URL: https://top-technologies.ru/ru/article/view?id=34030 (дата обращения: 22.11.2024).